tf

Transferfunktionsmodelle

Beschreibung

Verwenden Sie tf, um reellwertige oder komplexwertige Transferfunktionsmodelle zu erstellen oder um dynamische Systemmodelle in die Transferfunktionsform zu konvertieren.

Transferfunktionen sind eine Frequenzbereich-Darstellung linearer zeitinvarianter Systeme. Betrachten Sie zum Beispiel ein zeitkontinuierliches dynamisches SISO-System, das durch die Transferfunktion sys(s) = N(s)/D(s) dargestellt wird, wobei s = jw und N(s) und D(s) als Zähler- bzw. Nennerpolynome bezeichnet werden. Das tf-Modellobjekt kann SISO- oder MIMO-Transferfunktionen in kontinuierlicher Zeit oder diskreter Zeit darstellen.

Sie können ein Transferfunktions-Modellobjekt entweder durch direkte Angabe seiner Koeffizienten erstellen, oder durch Konvertierung eines Modells eines anderen Typs (z. B. eines Zustandsraummodells ss) in die Transferfunktionsform. Weitere Informationen finden Sie unter Transferfunktionen.

Sie können tf auch verwenden, um verallgemeinerte Zustandsraummodelle (genss) oder unsichere Zustandsraummodelle (uss (Robust Control Toolbox)) zu erstellen.

Erstellung

Syntax

sys = tf(numerator,denominator)

sys = tf(numerator,denominator,ts)

sys = tf(numerator,denominator,ltiSys)

sys = tf(m)

sys = tf(___,PropertyName=Value)

sys = tf(ltiSys)

sys = tf(ltiSys,Name=Value)

sys = tf(ltiSys,component)

s = tf('s')

z = tf('z',ts)

Beschreibung

Erstellen eines Transferfunktionsmodells

sys = tf(numerator,denominator) erstellt zunächst ein zeitkontinuierliches Transferfunktionsmodell, indem die Eigenschaften Numerator und Denominator angegeben werden. Betrachten Sie zum Beispiel ein zeitkontinuierliches dynamisches SISO-System, das durch die Transferfunktion sys(s) = N(s)/D(s) dargestellt wird, wobei die Eingangsargumente numerator und denominator die Koeffizienten von N(s) bzw. D(s) sind.

sys = tf(numerator,denominator,ts) erzeugt ein zeitdiskretes Transferfunktionsmodell und setzt die Eigenschaften Numerator, Denominator und Ts. Betrachten Sie zum Beispiel ein zeitdiskretes dynamisches SISO-System, das durch die Transferfunktion sys(z) = N(z)/D(z) dargestellt wird. Die Eingangsargumente numerator und denominator sind die Koeffizienten von N(z) bzw. D(z). Wenn Sie die Abtastzeit nicht angeben möchten, setzen Sie das Eingabeargument ts auf -1.

sys = tf(numerator,denominator,ltiSys) erstellt ein Transferfunktionsmodell mit Eigenschaften, die vom dynamischen Systemmodell ltiSys geerbt wurden, einschließlich der Abtastzeit.

sys = tf(m) erstellt ein Transferfunktionsmodell, das die statische Verstärkung m angibt.

sys = tf(___,PropertyName=Value) legt die Eigenschaften des Transferfunktionsmodells fest, indem es ein oder mehrere Eigenschaftsname-Wert-Argumente für eine der vorherigen Eingabe-Argument-Kombinationen verwendet.

Konvertieren in ein Transferfunktionsmodell

sys = tf(ltiSys) konvertiert das dynamische Systemmodell ltiSys in ein Transferfunktionsmodell.

sys = tf(ltiSys,Name=Value) erhält eine verkürzte Darstellung der Transferfunktion des schwach besetzten Modells ltiSys durch Berechnung der Nullstellen und Polstellen auf der Grundlage eines oder mehrerer angegebener Name-Wert-Argumente. Da diese Methode Nullstellen für jedes Eingangs-Ausgangs-Paar berechnet, ist sie am besten für Modelle mit kleinen Eingangs-Ausgangs-Größen geeignet. (seit R2025a)

sys = tf(ltiSys,component) konvertiert die angegebene Komponente component von ltiSys in die Form einer Transferfunktion. Verwenden Sie diese Syntax nur, wenn es sich bei ltiSys um ein identifiziertes lineares zeitinvariantes (LTI) Modell handelt.

Erstellen einer Variable für rationale Ausdrücke

s = tf('s') erzeugt eine spezielle Variable s, die Sie in einem rationalen Ausdruck verwenden können, um ein zeitkontinuierliches Transferfunktionsmodell zu erstellen. Die Verwendung eines rationalen Ausdrucks kann manchmal einfacher und intuitiver sein als die Angabe von Polynomkoeffizienten.

z = tf('z',ts) erzeugt eine spezielle Variable z, die Sie in einem rationalen Ausdruck verwenden können, um ein zeitkontinuierliches Transferfunktionsmodell zu erstellen. Wenn Sie die Abtastzeit nicht angeben möchten, setzen Sie das Eingabeargument ts auf -1.

Eingangsargumente

numerator — Zählerkoeffizienten der Transferfunktion

Zeilenvektor | NyxNu Zellenarray von Zeilenvektoren

Zählerkoeffizienten der Transferfunktion, angegeben als:

• Zeilenvektor aus Polynomkoeffizienten.

• Ein NyxNu-Zellenarray von Zeilenvektoren zur Angabe einer MIMO-Transferfunktion, wobei Ny die Anzahl der Ausgänge und Nu die Anzahl der Eingänge ist.

Wenn Sie die Transferfunktion erstellen, geben Sie die Zählerkoeffizienten in der Reihenfolge ihrer absteigenden Potenz an. Wenn der Zähler der Transferfunktion z. B. 3s^2-4s+5 lautet, geben Sie numerator als [3 -4 5] an. Für eine zeitdiskrete Transferfunktion mit Zähler 2z-1 setzen Sie numerator auf [2 -1].

Auch eine Eigenschaft des tf-Objekts. Weitere Informationen finden Sie unter Numerator.

denominator — Nennerkoeffizienten der Transferfunktion

Zeilenvektor | NyxNu Zellenarray von Zeilenvektoren

Nennerkoeffizienten, angegeben als:

• Zeilenvektor aus Polynomkoeffizienten.

• Ein NyxNu-Zellenarray von Zeilenvektoren zur Angabe einer MIMO-Transferfunktion, wobei Ny die Anzahl der Ausgänge und Nu die Anzahl der Eingänge ist.

Wenn Sie die Transferfunktion erstellen, geben Sie die Nennerkoeffizienten in der Reihenfolge ihrer absteigenden Potenz an. Wenn der Nenner der Transferfunktion z. B. 7s^2+8s-9 lautet, geben Sie denominator als [7 8 -9] an. Für eine zeitdiskrete Transferfunktion mit Nenner 2z^2+1 setzen Sie denominator auf [2 0 1].

Auch eine Eigenschaft des tf-Objekts. Weitere Informationen finden Sie unter Denominator.

ts — Abtastzeit

Skalar

Abtastzeit, angegeben als ein Skalar. Auch eine Eigenschaft des tf-Objekts. Weitere Informationen finden Sie unter Ts.

ltiSys — Dynamisches System

dynamisches Systemmodell | Modellarray

Dynamisches System, das als SISO- oder MIMO-Modell für dynamische Systeme oder als Array von dynamischen Systemmodellen angegeben wird. Zu den dynamischen Systemen, die Sie verwenden können, zählen:

• Zeitkontinuierliche oder zeitdiskrete numerische LTI-Modelle, wie tf, zpk, ss oder pid.

  Wenn ltiSys ein schwach besetztes Zustandsraummodell (sparss oder mechss) ist, berechnet die Software eine verkürzte Annäherung an die Transferfunktion, indem sie die Polstellen und Nullstellen in einem bestimmten Frequenzband des Fokus berechnet. Verwenden Sie für schwach besetzte Modelle die Name-Wert-Argumente, um Berechnungsoptionen festzulegen. Wenn Sie keine Optionen angeben, rechnet die Software bis zu den ersten 1000 Polstellen und Nullstellen mit dem kleinsten Betrag. Außerdem gilt diese Annäherung nur für Modelle mit einer gültigen sparss-Darstellung. (seit R2025a)

• Verallgemeinerte oder unsichere LTI-Modelle wie z. B. genss- oder uss (Robust Control Toolbox)-Modelle. (Für die Verwendung unsicherer Modelle ist die Software Robust Control Toolbox™ erforderlich.)

  Die resultierende Transferfunktion setzt Folgendes voraus:

  • aktuelle Werte der optimierbaren Komponenten für optimierbare Regelungsentwurf-Blöcke

  • nominale Modellwerte für unsichere Regelungsentwurf-Blöcke

• Identifizierte LTI-Modelle wie idtf (System Identification Toolbox)-, idss (System Identification Toolbox)-, idproc (System Identification Toolbox)-, idpoly (System Identification Toolbox)- und idgrey (System Identification Toolbox)-Modelle. Um die zu konvertierende Komponente des identifizierten Modells auszuwählen, geben Sie component an. Wenn Sie in component keine Komponente angeben, konvertiert tf standardmäßig die gemessene Komponente des identifizierten Modells. (Für die Verwendung von identifizierten Modellen ist die Software System Identification Toolbox™ erforderlich.)

m — Statische Verstärkung

Skalar | Matrix

Statische Verstärkung, angegeben als Skalar oder Matrix. Die statische Verstärkung (auch stationäre Verstärkung) eines Systems stellt das Verhältnis zwischen dem Ausgang und dem Eingang unter stationären Bedingungen dar.

component — Komponente des identifizierten Modells

'measured' (Standardeinstellung) | 'noise' | 'augmented'

Zu konvertierende Komponente des identifizierten Modells, angegeben als eine der folgenden Optionen:

• 'measured' – konvertiert die gemessene Komponente von sys.

• 'noise' – konvertiert die Rauschkomponente von sys

• 'augmented' – konvertiert sowohl die gemessene als auch die Rauschkomponente von sys.

component gilt nur, wenn sys ein identifiziertes LTI-Modell ist.

Weitere Informationen über identifizierte LTI-Modelle und ihre Mess- und Rauschkomponenten finden Sie unter Identified LTI Models.

Name-Wert-Argumente

Geben Sie optionale Argumentenpaare als Name1=Value1,...,NameN=ValueN an, wobei Name der Name des Arguments und Value der entsprechende Wert ist. Name-Werte-Argumente müssen nach anderen Argumenten erscheinen, aber die Reihenfolge der Paare spielt keine Rolle.

Beispiel: sys = tf(sparseSys,Focus=[0 100],Display="off")

UseParallel — Verwenden von paralleler Berechnung

0 oder false (Standardeinstellung) | 1 oder true

Seit R2025a

Verwenden Sie parallele Berechnung während der Nullstellen-Pol-Berechnung, angegeben als numerisches oder logisches 0 (false) oder 1(true).

Wenn UseParallel auf true eingestellt ist, können Sie sich explizit für die Skalierung auf Ihre bevorzugte parallele Umgebung entscheiden. Die Aktivierung der parallelen Berechnung kann zu einer verbesserten Leistung während der Nullstellen-Pol-Berechnung führen. Aber auch wenn UseParallel auf false eingestellt ist, kann der Algorithmus das eingebaute Multithreading verwenden, um die lokalen Ressourcen optimal zu nutzen. Weitere Informationen finden Sie unter MATLAB Multicore.

Diese Option erfordert eine Parallel Computing Toolbox™-Lizenz.

RollOff — Abfallrate

0 (Standardeinstellung) | nicht-positiver Skalar | Matrix

Seit R2025a

Abfallrate, angegeben als nicht-positiver Skalar oder Matrix.

• Verwenden Sie bei SISO-Modellen und bei MIMO-Modellen mit gleicher Steigung für alle Eingangs-Ausgangs-Paare einen skalaren Wert.

• Verwenden Sie eine Matrix, wenn die Steigung bei MIMO-Modellen für jedes Eingangs-Ausgangs-Paar unterschiedlich ist.

Mit dieser Option können Sie explizit angeben, wie die Annäherung über den angegebenen Frequenzbereich hinaus abfallen soll. Zum Beispiel stellt eine Steigung (Slope) von -2 sicher, dass die Verstärkung mit einer Rate von mindestens –40 dB/Dekade abfällt (eine Abfallrate von 1/s²) über fmax hinaus.

Focus — Frequenzbereich von Interesse

[0 Inf] (Standardeinstellung) | Vektor

Seit R2025a

Frequenzbereich von Interesse, angegeben als Vektor der Form [0,fmax]. Wenn Sie einen Frequenzbereich für den Fokus angeben, berechnet die Software nur die Polstellen mit einer Eigenfrequenz in diesem Bereich. Bei zeitdiskreten Modellen approximiert die Software die äquivalente Eigenfrequenz durch die Tustin-Transformation.

Da tf alle Polstellen und Nullstellen im angegebenen Frequenzbereich berechnet, geben Sie normalerweise einen niedrigen Frequenzbereich an, um die Berechnung einer großen Anzahl von Polstellen und Nullstellen zu begrenzen. Standardmäßig ist der Fokus nicht festgelegt ([0 Inf]) und der Algorithmus berechnet bis zu MaxNumber Polstellen und Nullstellen.

MaxNumber — Maximale Anzahl der zu berechnenden Polstellen und Nullstellen

1000 (Standardeinstellung) | positive ganze Zahl

Seit R2025a

Maximale Anzahl der zu berechnenden Polstellen und Nullstellen, angegeben als positive Ganzzahl. Dieser Wert begrenzt die Anzahl der vom Algorithmus berechneten Polstellen und Nullstellen und die Ordnung der Annäherung an das ursprüngliche schwach besetzte Modell.

Shift — Spektralverschiebung

0 (Standardeinstellung) | endlicher Skalar

Seit R2025a

Spektralverschiebung, angegeben als endlicher Skalar.

Die Software berechnet Polstellen mit der Eigenfrequenz im angegebenen Bereich [0,fmax] unter Verwendung von Iterationen der inversen Potenz für A-sigma*E, wodurch Eigenwerte erhalten werden, die am nächsten an der Verschiebung sigma liegen. Wenn A singulär und sigma null ist, schlägt der Algorithmus fehl, da keine Inverse existiert. Daher können Sie für schwach besetzte Modelle mit integraler Wirkung (s = 0 oder bei z = 1 für zeitdiskrete Modelle) diese Option verwenden, um implizit Polstellen oder Nullstellen auf den Wert zu verschieben, der diesem Verschiebungswert am nächsten liegt. Geben Sie einen Verschiebungswert an, der nicht gleich einem vorhandenen Pol- oder Nullwert des Originalmodells ist.

Tolerance — Genauigkeit der berechneten Polstellen und Nullstellen

1e-12 (Standardeinstellung) | positiver endlicher Skalar

Seit R2025a

Toleranz für die Genauigkeit der berechneten Polstellen und Nullstellen, angegeben als positiver endlicher Skalar. Dieser Wert steuert die Konvergenz der berechneten Eigenwerte in den Iterationen der inversen Potenz.

Display — Anzeigen oder Ausblenden des Fortschrittsberichts

"on" (Standardeinstellung) | "off"

Seit R2025a

Fortschrittsbericht anzeigen oder ausblenden, angegeben als "off" oder "on".

Ausgangsargumente

sys — Ausgang des Systemmodells

tf-Modellobjekt | genss Modellobjekt | uss Modellobjekt

Ausgang des Systemmodells, geliefert als:

• Eine Transferfunktion (tf) ist ein Modellobjekt, wenn die Eingangsargumente numerator und denominator numerische Arrays sind. sys ist immer ein tf-Modellobjekt, wenn die eine Konvertierung des Modelltyps von ltiSys zu tf stattfindet.

• Ein verallgemeinertes Zustandsraum-Modellobjekt (genss), wenn die Eingangsargumente numerator oder denominator optimierbare Parameter enthalten, wie z. B. realp-Parameter oder verallgemeinerte Matrizen (genmat). Ein Beispiel hierzu finden Sie unter Optimierbarer Tiefpassfilter.

• Ein unsicheres Zustandsraum-Modellobjekt (uss), wenn die Eingangsargumente numerator oder denominator unsichere Parameter enthalten. Für die Verwendung unsicherer Modelle ist die Software Robust Control Toolbox erforderlich. Ein Beispiel hierzu finden Sie unter Transfer Function with Uncertain Coefficients (Robust Control Toolbox).

Eigenschaften

Numerator — Zählerkoeffizienten

Zeilenvektor | NyxNu Zellenarray von Zeilenvektoren

Zählerkoeffizienten, angegeben als:

• Zeilenvektor von Polynomkoeffizienten in absteigender Potenz (für Variable-Werte 's', 'z', 'p' oder 'q') oder in aufsteigender Potenz (für Variable-Werte 'z^-1' oder 'q^-1').

• Ein NyxNu-Zellenarray von Zeilenvektoren zur Angabe einer MIMO-Transferfunktion, wobei Ny die Anzahl der Ausgänge und Nu die Anzahl der Eingänge ist. Jedes Element des Zellenarrays gibt die Zählerkoeffizienten für ein bestimmtes Eingangs-/Ausgangspaar an. Wenn Sie sowohl Numerator als auch Denominator als Zellenarray angeben, müssen sie die gleichen Dimensionen haben.

Die Koeffizienten von Numerator können entweder reell oder komplexwertig sein.

Denominator — Nennerkoeffizienten

Zeilenvektor | NyxNu Zellenarray von Zeilenvektoren

Nennerkoeffizienten, angegeben als:

• Ein Zeilenvektor von Polynomkoeffizienten in absteigender Potenz (für Variable-Werte 's', 'z', 'p' oder 'q') oder in aufsteigender Potenz (für Variable-Werte 'z^-1' oder 'q^-1').

• Ein NyxNu-Zellenarray von Zeilenvektoren zur Angabe einer MIMO-Transferfunktion, wobei Ny die Anzahl der Ausgänge und Nu die Anzahl der Eingänge ist. Jedes Element des Zellenarrays gibt die Zählerkoeffizienten für ein bestimmtes Eingangs-/Ausgangspaar an. Wenn Sie sowohl Numerator als auch Denominator als Zellenarray angeben, müssen sie die gleichen Dimensionen haben.

Wenn alle SISO-Einträge einer MIMO-Transferfunktion denselben Nenner haben, können Sie Denominator als Zeilenvektor angeben, während Sie Numerator als Zellenarray angeben.

Die Koeffizienten von Denominator können entweder reell oder komplexwertig sein.

Variable — Anzeigevariable der Transferfunktion

's' (Standardeinstellung) | 'z' | 'p' | 'q' | 'z^-1' | 'q^-1'

Anzeigevariable der Transferfunktion, angegeben als eine der folgenden Optionen:

• 's' – Standard für zeitkontinuierliche Modelle

• 'z' – Standard für zeitdiskrete Modelle

• 'p' – äquivalent zu 's'

• 'q' – äquivalent zu 'z'

• 'z^-1' – invers zu 'z'

• 'q^-1' – äquivalent zu 'z^-1'

Der Wert von Variable wird in der Anzeige widergespiegelt und wirkt sich bei zeitdiskreten Modellen auch auf die Interpretation der Koeffizientenvektoren von Numerator und Denominator aus.

• Für die Variable-Werte 's', 'z', 'p' oder 'q' werden die Koeffizienten in absteigenden Potenzen der Variablen geordnet. Betrachten Sie zum Beispiel den Zeilenvektor [ak ... a1 a0]. Die Polynomreihenfolge wird als $$a_k{z}^k+\mathrm{...}+a_{1}z+a_0$$ angegeben.

• Für die Variable-Werte 'z^-1' oder 'q^-1' werden die Koeffizienten in aufsteigenden Potenzen der Variablen geordnet. Betrachten Sie zum Beispiel den Zeilenvektor [b0 b1 ... bk]. Die Polynomreihenfolge wird als $$b_0+b_1{z}^{-1}+\mathrm{...}+b_k{z}^{-k}$$ angegeben.

Beispiele finden Sie unter Angabe der polynomischen Ordnung einer zeitdiskreten Transferfunktion, Transferfunktionsmodelle unter Verwendung rationaler Ausdrücke und Zeitkontinuierliches Transferfunktionsmodell unter Verwendung rationaler Ausdrücke.

IODelay — Transportverzögerung

0 (Standardeinstellung) | Skalar | NyxNu-Array

Transportverzögerung, die als eine der folgenden Optionen angegeben wird:

• Skalar: Geben Sie die Transportverzögerung für ein SISO-System oder die gleiche Transportverzögerung für alle Eingangs-/Ausgangspaare eines MIMO-Systems an.

• NyxNu-Array: Geben Sie separate Transportverzögerungen für jedes Eingangs-/Ausgangspaar eines MIMO-Systems an. Dabei ist Ny die Anzahl der Ausgänge und Nu die Anzahl der Eingänge.

Für zeitkontinuierliche Systeme geben Sie die Transportverzögerungen in der Zeiteinheit an, die durch die Eigenschaft TimeUnit festgelegt ist. Für zeitdiskrete Systeme geben Sie die Transportverzögerungen in ganzzahligen Vielfachen der Abtastzeit Ts an.

InputDelay — Eingangsverzögerung

0 (Standardeinstellung) | Skalar | Nux1-Vektor

Eingangsverzögerung für jeden Eingangskanal, die als eine der folgenden Optionen angegeben wird:

• Skalar: Geben Sie die Eingangsverzögerung für ein SISO-System oder die gleiche Transportverzögerung für alle Eingänge eines Systems mit mehreren Eingängen an.

• Nux1-Vektor: Geben Sie separate Eingangsverzögerungen für die Eingänge eines Systems mit mehreren Eingängen an, wobei Nu die Anzahl der Eingänge ist.

Für zeitkontinuierliche Systeme geben Sie die Eingangsverzögerungen in der Zeiteinheit an, die durch die Eigenschaft TimeUnit festgelegt ist. Für zeitdiskrete Systeme geben Sie die Eingangsverzögerungen in ganzzahligen Vielfachen der Abtastzeit Ts an.

Weitere Informationen finden Sie unter Time Delays in Linear Systems.

OutputDelay — Ausgangsverzögerung

0 (Standardeinstellung) | Skalar | Nyx1-Vektor

Ausgangsverzögerung für jeden Ausgangskanal, die als eine der folgenden Optionen angegeben wird:

• Skalar: Geben Sie die Ausgangsverzögerung für ein SISO-System oder die gleiche Verzögerung für alle Ausgänge eines Systems mit mehreren Ausgängen an.

• Nyx1-Vektor: Geben Sie separate Ausgangsverzögerungen für die Ausgänge eines Systems mit mehreren Ausgängen an, wobei Ny die Anzahl der Ausgänge ist.

Für zeitkontinuierliche Systeme geben Sie die Ausgangsverzögerungen in der Zeiteinheit an, die durch die Eigenschaft TimeUnit festgelegt ist. Für zeitdiskrete Systeme geben Sie die Ausgangsverzögerungen in ganzzahligen Vielfachen der Abtastzeit Ts an.

Weitere Informationen finden Sie unter Time Delays in Linear Systems.

Ts — Abtastzeit

0 (Standardeinstellung) | Positiver Skalar | -1

Abtastzeit, angegeben als:

• 0 bei zeitkontinuierlichen Systemen.

• Ein positiver Skalar, der die Abtastzeit eines zeitdiskreten Systems angibt. Geben Sie Ts in der Zeiteinheit an, die durch die Eigenschaft TimeUnit festgelegt ist.

• -1 für ein zeitdiskretes System mit einer nicht festgelegten Abtastzeit.

Hinweis

Eine Änderung von Ts bewirkt keine Diskretisierung oder Neuabtastung des Modells. Verwenden Sie zur Konvertierung zwischen zeitkontinuierlichen und zeitdiskreten Systemen c2d und d2c. Verwenden Sie d2d, um die Abtastzeit eines zeitdiskreten Systems zu ändern.

TimeUnit — Einheiten der Zeitvariablen

'seconds' (Standardeinstellung) | 'nanoseconds' | 'microseconds' | 'milliseconds' | 'minutes' | 'hours' | 'days' | 'weeks' | 'months' | 'years' | ...

Die Zeitvariablen können folgende Einheiten haben:

• 'nanoseconds'

• 'microseconds'

• 'milliseconds'

• 'seconds'

• 'minutes'

• 'hours'

• 'days'

• 'weeks'

• 'months'

• 'years'

Die Änderung von TimeUnit hat keine Auswirkungen auf andere Eigenschaften, ändert aber das gesamte Systemverhalten. Verwenden Sie chgTimeUnit, um zwischen Zeiteinheiten zu konvertieren, ohne das Systemverhalten zu ändern.

InputName — Namen der Eingangskanäle

'' (Standardeinstellung) | Zeichenvektor | Zellenarray von Zeichenvektoren

Namen der Eingangskanäle, die als eine der folgenden Optionen angegeben werden:

• Zeichenvektor, für Modelle mit einem Eingang.

• Zellenarray von Zeichenvektoren, für Modelle mit mehreren Eingängen.

• '', ohne Angabe von Namen, für beliebige Eingangskanäle.

Sie können aber auch Eingangsnamen für Modelle mit mehreren Eingängen mithilfe der automatischen Vektorerweiterung zuweisen. Wenn sys zum Beispiel ein Modell mit zwei Eingängen ist, geben Sie Folgendes ein.

sys.InputName = 'controls';

Die Eingangsnamen werden automatisch zu {'controls(1)';'controls(2)'} erweitert.

Sie können die Kurzschreibweise u verwenden, um auf die Eigenschaft InputName zu verweisen. Beispielsweise ist sys.u gleichbedeutend mit sys.InputName.

Verwenden Sie InputName, um:

• Kanäle auf der Modellanzeige und in Diagrammen zu identifizieren.

• Subsysteme von MIMO-Systemen zu extrahieren.

• Verbindungspunkte festzulegen, wenn Sie Modelle miteinander verbinden.

InputUnit — Einheiten der Eingangskanäle

'' (Standardeinstellung) | Zeichenvektor | Zellenarray von Zeichenvektoren

Die Eingangskanäle können folgende Einheiten haben:

• Zeichenvektor, für Modelle mit einem Eingang.

• Zellenarray von Zeichenvektoren, für Modelle mit mehreren Eingängen.

• '', ohne Angabe von Einheiten, für beliebige Eingangskanäle.

Verwenden Sie InputUnit, um die Einheiten des Eingangssignals anzugeben. InputUnit hat keine Auswirkung auf das Systemverhalten.

InputGroup — Eingangskanalgruppen

Struktur

Eingangskanalgruppen, angegeben als Struktur. Verwenden Sie InputGroup, um die Eingangskanäle von MIMO-Systemen in Gruppen einzuteilen und jede Gruppe mit einem Namen zu versehen. Die Feldnamen von InputGroup sind die Gruppennamen und die Feldwerte sind die Eingangskanäle der einzelnen Gruppen. Geben Sie zum Beispiel Folgendes ein, um Eingangsgruppen mit den Namen controls und noise zu erstellen, die die Eingangskanäle 1 und 2 bzw. 3 und 5 enthalten.

sys.InputGroup.controls = [1 2];
sys.InputGroup.noise = [3 5];

Sie können dann das Subsystem von den controls-Eingängen auf alle Ausgänge extrahieren, indem Sie Folgendes verwenden:

sys(:,'controls')

Standardmäßig ist InputGroup eine Struktur ohne Felder.

OutputName — Namen der Ausgangskanäle

'' (Standardeinstellung) | Zeichenvektor | Zellenarray von Zeichenvektoren

Namen der Ausgangskanäle, die als eine der folgenden Optionen angegeben werden:

• Zeichenvektor, für Modelle mit einem Ausgang.

• Zellenarray von Zeichenvektoren, für Modelle mit mehreren Ausgängen.

• '', ohne Angabe von Namen, für beliebige Ausgangskanäle.

Sie können aber auch Ausgangsnamen für Modelle mit mehreren Ausgängen mithilfe der automatischen Vektorerweiterung zuweisen. Wenn sys zum Beispiel ein Modell mit zwei Ausgängen ist, geben Sie Folgendes ein:

sys.OutputName = 'measurements';

Die Ausgangsnamen werden automatisch zu {'measurements(1)';'measurements(2)'} erweitert.

Sie können auch die Kurzschreibweise y verwenden, um auf die Eigenschaft OutputName zu verweisen. Beispielsweise ist sys.y gleichbedeutend mit sys.OutputName.

Verwenden Sie OutputName, um:

• Kanäle auf der Modellanzeige und in Diagrammen zu identifizieren.

• Subsysteme von MIMO-Systemen zu extrahieren.

• Verbindungspunkte festzulegen, wenn Sie Modelle miteinander verbinden.

OutputUnit — Einheiten der Ausgangskanäle

'' (Standardeinstellung) | Zeichenvektor | Zellenarray von Zeichenvektoren

Die Ausgangskanäle können folgende Einheiten haben:

• Zeichenvektor, für Modelle mit einem Ausgang.

• Zellenarray von Zeichenvektoren, für Modelle mit mehreren Ausgängen.

• '', ohne Angabe von Einheiten, für beliebige Ausgangskanäle.

Verwenden Sie OutputUnit, um die Einheiten des Ausgangssignals anzugeben. OutputUnit hat keine Auswirkung auf das Systemverhalten.

OutputGroup — Ausgangskanalgruppen

Struktur

Ausgangskanalgruppen, angegeben als Struktur. Verwenden Sie OutputGroup, um die Ausgangskanäle von MIMO-Systemen in Gruppen einzuteilen und jede Gruppe mit einem Namen zu versehen. Die Feldnamen von OutputGroup sind die Gruppennamen und die Feldwerte sind die Ausgangskanäle der einzelnen Gruppen. Geben Sie zum Beispiel Folgendes ein, um Ausgangsgruppen mit den Namen temperature und measurement zu erstellen, die die Ausgangskanäle 1 bzw. 3 bzw. 5 enthalten.

sys.OutputGroup.temperature = [1];
sys.OutputGroup.measurement = [3 5];

Sie können dann das Subsystem von allen Eingängen in die measurement-Ausgänge extrahieren, indem Sie Folgendes verwenden:

sys('measurement',:)

Standardmäßig ist OutputGroup eine Struktur ohne Felder.

Name — Systemname

'' (Standardeinstellung) | Zeichenvektor

Systemname, angegeben als Zeichenvektor. Zum Beispiel: 'system_1'.

Notes — Benutzerspezifischer Text

{} (Standardeinstellung) | Zeichenvektor | Zellenarray von Zeichenvektoren

Vom Benutzer angegebener Text, den Sie mit dem System verknüpfen möchten, angegeben als Zeichenvektor oder Zellenarray von Zeichenvektoren. Zum Beispiel: 'System is MIMO'.

UserData — Benutzerspezifische Daten

[] (Standardeinstellung) | beliebiger MATLAB^®-Datentyp

Benutzerspezifische Daten, die Sie mit dem System verknüpfen möchten, angegeben als beliebiger MATLAB-Datentyp.

SamplingGrid — Abtastgitter für Modellarrays

Struktur-Array

Abtastgitter für Modellarrays, angegeben als Struktur-Array.

Verwenden Sie SamplingGrid, um die Variablenwerte zu verfolgen, die mit jedem Modell in einem Modellarray verbunden sind, einschließlich identifizierter linearer zeitinvarianter Modellarrays (IDLTI-Modellarrays).

Setzen Sie die Feldnamen der Struktur auf die Namen der Abtastvariablen. Setzen Sie die Feldwerte auf die Werte der Abtastvariablen, die mit jedem Modell im Array verbunden sind. Alle Abtastvariablen müssen numerische Skalare sein und alle Arrays der Abtastwerte müssen den Dimensionen des Modellarrays entsprechen.

Sie können zum Beispiel ein 11x1-Array mit linearen Modellen, sysarr, erstellen, indem Sie Schnappschüsse eines linearen zeitvariablen Systems zu den Zeiten t = 0:10 machen. Der folgende Code speichert die Zeitabtastungen mit den linearen Modellen.

 sysarr.SamplingGrid = struct('time',0:10)

In ähnlicher Weise können Sie ein 6x9-Modellarray M erstellen, indem Sie zwei Variablen, zeta und w, unabhängig voneinander abtasten. Der folgende Code ordnet die (zeta,w)-Werte M zu.

[zeta,w] = ndgrid(<6 values of zeta>,<9 values of w>)
M.SamplingGrid = struct('zeta',zeta,'w',w)

Wenn Sie M anzeigen, enthält jeder Eintrag im Array die entsprechenden Werte für zeta und w.

M

M(:,:,1,1) [zeta=0.3, w=5] =
 
        25
  --------------
  s^2 + 3 s + 25
 

M(:,:,2,1) [zeta=0.35, w=5] =
 
         25
  ----------------
  s^2 + 3.5 s + 25
 
...

Bei Modellarrays, die durch die Linearisierung eines Simulink^®-Modells bei mehreren Parameterwerten oder Betriebspunkten erzeugt werden, füllt die Software das SamplingGrid automatisch mit den Variablenwerten auf, die den einzelnen Einträgen im Array entsprechen. Zum Beispiel füllen die Simulink Control Design™-Befehle linearize (Simulink Control Design) und slLinearizer (Simulink Control Design) das SamplingGrid automatisch auf.

Standardmäßig handelt es sich bei SamplingGrid um eine Struktur ohne Felder.

Objektfunktionen

Die folgenden Listen enthalten eine repräsentative Teilmenge der Funktionen, die Sie mit tf-Modellen verwenden können. Im Allgemeinen ist jede Funktion, die auf Dynamische Systemmodelle anwendbar ist, auch auf ein tf-Objekt anwendbar.

Lineare Analyse

step	Sprungantwort eines dynamischen Systems
impulse	Impulse response plot of dynamic system; impulse response data
lsim	Compute time response simulation data of dynamic system to arbitrary inputs
bode	Bode-Frequenzgang eines dynamischen Systems
nyquist	Nyquist-Antwort eines dynamischen Systems
nichols	Nichols response of dynamic system
bandwidth	Frequency response bandwidth

Stabilitätsanalyse

pole	Poles of dynamic system
zero	Zeros and gain of SISO dynamic system
pzplot	Plot pole-zero map of dynamic system
margin	Amplitudenrand, Phasenrand und Übergangsfrequenzen

Modelltransformation

zpk	Zero-pole-gain model
ss	Zustandsraummodell
c2d	Konvertieren eines Modells von kontinuierlicher zu diskreter Zeit
d2c	Convert model from discrete to continuous time
d2d	Resample discrete-time model

Modellverbindung

feedback	Feedback-Verbindung mehrere Modelle
connect	Block diagram interconnections of dynamic systems
series	Reihenschaltung von zwei Modellen
parallel	Parallel connection of two models

Reglerentwurf

pidtune	PID tuning algorithm for linear plant model
rlocus	Wurzelort dynamischer Systeme
lqr	Entwurf eines linear-quadratischen Reglers (LQR)
lqg	Linear-Quadratic-Gaussian (LQG) design
lqi	Linear-quadratisch-integrale Steuerung
kalman	Design Kalman filter for state estimation

Beispiele

SISO-Transferfunktionsmodelle

Betrachten Sie in diesem Beispiel das folgende SISO-Transferfunktionsmodell:

$$sys(s)=\frac{1}{2s^2+3s+4}.$$

Geben Sie die Zähler- und Nennerkoeffizienten in absteigenden Potenzen von s an und erstellen Sie das Transferfunktionsmodell.

numerator = 1;
denominator = [2,3,4];
sys = tf(numerator,denominator)

sys =
 
         1
  ---------------
  2 s^2 + 3 s + 4
 
Continuous-time transfer function.
Model Properties

Zeitdiskretes SISO-Transferfunktionsmodell

Betrachten Sie in diesem Beispiel das folgende zeitdiskrete SISO-Transferfunktionsmodell:

$$sys(z)=\frac{2z}{4z^3+3z-1}.$$

Geben Sie die Zähler- und Nennerkoeffizienten in absteigenden Potenzen von z an und verwenden Sie eine Abtastzeit von 0,1 Sekunden. Erstellen Sie das zeitdiskrete Transferfunktionsmodell.

numerator = [2,0];
denominator = [4,0,3,-1];
ts = 0.1;
sys = tf(numerator,denominator,ts)

sys =
 
        2 z
  ---------------
  4 z^3 + 3 z - 1
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Transferfunktion zweiter Ordnung aus Dämpfungsverhältnis und Eigenfrequenz

Betrachten Sie in diesem Beispiel ein Transferfunktionsmodell, das ein System zweiter Ordnung mit bekannter Eigenfrequenz und bekanntem Dämpfungsverhältnis darstellt.

Die Transferfunktion eines Systems zweiter Ordnung, ausgedrückt durch das Dämpfungsverhältnis $$\zeta$$ und die Eigenfrequenz $${\omega }_0$$ lautet:

$$sys\left(s\right)=\frac{{\omega }_0^2}{s^2+2\zeta {\omega }_{0}s+{\omega }_0^2}.$$

Unter der Annahme des Dämpfungsverhältnisses $$\zeta$$ = 0.25 und der Eigenfrequenz $${\omega }_0$$ = 3 rad/s, erstellen Sie die Transferfunktion zweiter Ordnung.

zeta = 0.25;
w0 = 3;
numerator = w0^2;
denominator = [1,2*zeta*w0,w0^2];
sys = tf(numerator,denominator)

sys =
 
         9
  ---------------
  s^2 + 1.5 s + 9
 
Continuous-time transfer function.
Model Properties

Untersuchen Sie die Antwort dieser Transferfunktion auf einen Eingangssprung.

stepplot(sys)

Das Diagramm zeigt das erwartete Abklingen eines Systems zweiter Ordnung mit einem geringen Dämpfungsverhältnis.

Zeitdiskretes MIMO-Transferfunktionsmodell

Erstellen Sie ein Transferfunktionsmodell für das folgende zeitdiskrete Modell mit mehreren Ein- und Ausgängen:

$$sys\left(z\right)=\left[\begin{array}{cc}\frac{1}{z+0.3}& \frac{z}{z+0.3}\\ \frac{-z+2}{z+0.3}& \frac{3}{z+0.3}\end{array}\right]$$

mit einer Abtastzeit von ts = 0.2 Sekunden.

Geben Sie die Zählerkoeffizienten als 2x2-Matrix an.

numerators = {1 [1 0];[-1 2] 3};

Geben Sie die Koeffizienten des gemeinsamen Nenners als Zeilenvektor an.

denominator = [1 0.3];

Erstellen Sie das zeitdiskrete MIMO-Transferfunktionsmodell.

ts = 0.2;
sys = tf(numerators,denominator,ts)

sys =
 
  From input 1 to output...
          1
   1:  -------
       z + 0.3
 
       -z + 2
   2:  -------
       z + 0.3
 
  From input 2 to output...
          z
   1:  -------
       z + 0.3
 
          3
   2:  -------
       z + 0.3
 
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties

Weitere Informationen zur Erstellung von MIMO-Transferfunktionen finden Sie unter MIMO-Transferfunktionen.

Verkettung von SISO-Transferfunktionen zu MIMO-Transferfunktionsmodellen

In diesem Beispiel erstellen Sie ein MIMO-Transferfunktionsmodell durch Verkettung von SISO-Transferfunktionsmodellen. Betrachten Sie die folgende Transferfunktion mit einem Eingang und zwei Ausgängen:

$$sys(s)=\left[\begin{array}{c}\frac{s-1}{s+1}\\ \frac{s+2}{s^2+4s+5}\end{array}\right].$$

Geben Sie das MIMO-Transferfunktionsmodell an, indem Sie die SISO-Einträge verketten.

sys1 = tf([1 -1],[1 1]);		
sys2 = tf([1 2],[1 4 5]);
sys = [sys1;sys2]

sys =
 
  From input to output...
       s - 1
   1:  -----
       s + 1
 
           s + 2
   2:  -------------
       s^2 + 4 s + 5
 
Continuous-time transfer function.
Model Properties

Weitere Informationen zur Erstellung von MIMO-Transferfunktionen finden Sie unter MIMO-Transferfunktionen.

Transferfunktionsmodelle unter Verwendung rationaler Ausdrücke

In diesem Beispiel erstellen Sie ein zeitkontinuierliches Transferfunktionsmodell unter Verwendung rationaler Ausdrücke. Die Verwendung eines rationalen Ausdrucks kann manchmal einfacher und intuitiver sein als die Angabe von Polynomkoeffizienten für Zähler und Nenner.

Betrachten Sie das folgende System:

$$sys(s)=\frac{s}{s^2+2s+10}.$$

Um das Transferfunktionsmodell zu erstellen, geben Sie zunächst s als tf-Objekt an.

s = tf('s')

s =
 
  s
 
Continuous-time transfer function.
Model Properties

Erstellen Sie das Transferfunktionsmodell unter Verwendung von s im rationalen Ausdruck.

sys = s/(s^2 + 2*s + 10)

sys =
 
        s
  --------------
  s^2 + 2 s + 10
 
Continuous-time transfer function.
Model Properties

Zeitkontinuierliches Transferfunktionsmodell unter Verwendung rationaler Ausdrücke

In diesem Beispiel erstellen Sie ein zeitdiskretes Transferfunktionsmodell unter Verwendung eines rationalen Ausdrucks. Die Verwendung eines rationalen Ausdrucks kann manchmal einfacher und intuitiver sein als die Angabe von Polynomkoeffizienten.

Betrachten Sie das folgende System:

$$sys(z)=\frac{z-1}{z^2-1.85z+0.9}.$$

Um das Transferfunktionsmodell zu erstellen, geben Sie zunächst z als tf-Objekt und die Abtastzeit Ts an.

ts = 0.1;
z = tf('z',ts)

z =
 
  z
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Erstellen Sie das Transferfunktionsmodell unter Verwendung von z im rationalen Ausdruck.

sys = (z - 1) / (z^2 - 1.85*z + 0.9)

sys =
 
        z - 1
  ------------------
  z^2 - 1.85 z + 0.9
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Transferfunktionsmodell mit geerbten Eigenschaften

Für dieses Beispiel erstellen Sie ein Transferfunktionsmodell mit Eigenschaften, die von einem anderen Transferfunktionsmodell geerbt wurden. Betrachten Sie die folgenden beiden Transferfunktionen:

$$sys1(s)=\frac{2s}{s^2+8s}andsys2(s)=\frac{s-1}{7s^4+2s^3+9}.$$

In diesem Beispiel erstellen Sie sys1, wobei die Eigenschaften TimeUnit und InputDelay auf 'minutes' eingestellt sind.

numerator1 = [2,0];
denominator1 = [1,8,0];
sys1 = tf(numerator1,denominator1,'TimeUnit','minutes','InputUnit','minutes')

sys1 =
 
     2 s
  ---------
  s^2 + 8 s
 
Continuous-time transfer function.
Model Properties

propValues1 = [sys1.TimeUnit,sys1.InputUnit]

propValues1 = 1×2 cell
    {'minutes'}    {'minutes'}

Erstellen Sie das zweite Transferfunktionsmodell mit den von sys1 geerbten Eigenschaften.

numerator2 = [1,-1];
denominator2 = [7,2,0,0,9];
sys2 = tf(numerator2,denominator2,sys1)

sys2 =
 
        s - 1
  -----------------
  7 s^4 + 2 s^3 + 9
 
Continuous-time transfer function.
Model Properties

propValues2 = [sys2.TimeUnit,sys2.InputUnit]

propValues2 = 1×2 cell
    {'minutes'}    {'minutes'}

Beachten Sie, dass das Transferfunktionsmodell sys2 die gleichen Eigenschaften hat wie sys1.

Array von Transferfunktionsmodellen

Sie können eine for-Schleife verwenden, um ein Array von Transferfunktionsmodellen anzugeben.

Legen Sie zunächst das Array der Transferfunktionen mit Nullstellen an.

sys = tf(zeros(1,1,3));

Die ersten beiden Indizes stehen für die Anzahl der Ausgänge und Eingänge der Modelle, während der dritte Index die Anzahl der Modelle im Array angibt.

Erstellen Sie das Array für die Transferfunktion mithilfe eines rationalen Ausdrucks in der for-Schleife.

s = tf('s');                                                  
for k = 1:3                                                             
    sys(:,:,k) = k/(s^2+s+k);                                          
end
sys

sys(:,:,1,1) =
 
       1
  -----------
  s^2 + s + 1
 

sys(:,:,2,1) =
 
       2
  -----------
  s^2 + s + 2
 

sys(:,:,3,1) =
 
       3
  -----------
  s^2 + s + 3
 
3x1 array of continuous-time transfer functions.
Model Properties

Konvertieren des Zustandsraummodells in eine Transferfunktion

Berechnen Sie in diesem Beispiel die Transferfunktion des folgenden Zustandsraummodells:

$$A=\left[\begin{array}{cc}-2& -1\\ 1& -2\end{array}\right],B=\left[\begin{array}{cc}1& 1\\ 2& -1\end{array}\right],C=\left[\begin{array}{cc}1& 0\end{array}\right],D=[\begin{array}{cc}0& 1\end{array}].$$

Erstellen Sie das Zustandsraummodell unter Verwendung der Zustandsraummatrizen.

A = [-2 -1;1 -2];
B = [1 1;2 -1];
C = [1 0];
D = [0 1];
ltiSys = ss(A,B,C,D);

Konvertieren Sie das Zustandsraummodell ltiSys in eine Transferfunktion.

sys = tf(ltiSys)

sys =
 
  From input 1 to output:
        s
  -------------
  s^2 + 4 s + 5
 
  From input 2 to output:
  s^2 + 5 s + 8
  -------------
  s^2 + 4 s + 5
 
Continuous-time transfer function.
Model Properties

Extrahieren der Transferfunktionen aus identifiziertem Modell

In diesem Beispiel extrahieren Sie die gemessenen Komponenten und die Rauschkomponenten eines identifizierten Polynommodells in zwei separate Transferfunktionen.

Laden Sie das Box-Jenkins-Polynommodell ltiSys in identifiedModel.mat.

load('identifiedModel.mat','ltiSys');

ltiSys ist ein identifiziertes zeitdiskretes Modell der Form: $$y(t)=\frac{B}{F}u(t)+\frac{C}{D}e(t)$$, wobei $$\frac{B}{F}$$ die gemessene Komponente und $$\frac{C}{D}$$ die Rauschkomponente darstellt.

Extrahieren Sie die gemessenen Komponenten und die Rauschkomponenten als Transferfunktionen.

sysMeas = tf(ltiSys,'measured') 

sysMeas =
 
  From input "u1" to output "y1":
            -0.1426 z^-1 + 0.1958 z^-2
  z^(-2) * ----------------------------
           1 - 1.575 z^-1 + 0.6115 z^-2
 
Sample time: 0.04 seconds
Discrete-time transfer function.
Model Properties

sysNoise = tf(ltiSys,'noise')

sysNoise =
 
  From input "v@y1" to output "y1":
           0.04556 + 0.03301 z^-1
  ----------------------------------------
  1 - 1.026 z^-1 + 0.26 z^-2 - 0.1949 z^-3
 
Input groups:        
    Name     Channels
    Noise       1    
                     
Sample time: 0.04 seconds
Discrete-time transfer function.
Model Properties

Die gemessene Komponente kann als Regelstreckenmodell dienen, während die Rauschkomponente als Störungsmodell für den Entwurf des Regelungssystems verwendet werden kann.

Angabe der Namen der Eingänge und Ausgänge des MIMO-Transferfunktionsmodells

Transferfunktions-Modellobjekte enthalten Modelldaten, die Ihnen helfen, den Überblick darüber zu behalten, was das Modell darstellt. So können Sie beispielsweise den Eingängen und Ausgängen Ihres Modells Namen zuweisen.

Betrachten Sie das folgende zeitdiskrete MIMO-Transferfunktionsmodell:

$$sys(s)=\left[\begin{array}{c}\frac{s+1}{s^2+2s+2}\\ \frac{1}{s}\end{array}\right]$$

Dieses Modell hat einen Eingang $$-$$, Strom, und zwei Ausgänge $$-$$, Drehmoment und Winkelgeschwindigkeit.

Geben Sie zunächst die Zähler- und Nennerkoeffizienten des Modells an.

numerators = {[1 1] ; 1};
denominators = {[1 2 2] ; [1 0]};

Erstellen Sie das Transferfunktionsmodell und geben Sie die Namen der Eingänge und Ausgänge an.

sys = tf(numerators,denominators,'InputName','Current',...
        'OutputName',{'Torque' 'Angular Velocity'})

sys =
 
  From input "Current" to output...
                s + 1
   Torque:  -------------
            s^2 + 2 s + 2
 
                      1
   Angular Velocity:  -
                      s
 
Continuous-time transfer function.
Model Properties

Angabe der polynomischen Ordnung einer zeitdiskreten Transferfunktion

In diesem Beispiel legen Sie die polynomiale Ordnung in zeitdiskreten Transferfunktionsmodellen mithilfe der Eigenschaft 'Variable' fest.

Betrachten Sie die folgenden zeitdiskreten Transferfunktionen mit einer Abtastzeit von 0,1 Sekunden:

$$sys1(z)=\frac{z^2}{z^2+2z+3}sys2(z^{-1})=\frac{1}{1+2z^{-1}+3z^{-2}}.$$

Erstellen Sie die erste zeitdiskrete Transferfunktion, indem Sie die z-Koeffizienten angeben.

numerator = [1,0,0];
denominator = [1,2,3];
ts = 0.1;
sys1 = tf(numerator,denominator,ts)

sys1 =
 
       z^2
  -------------
  z^2 + 2 z + 3
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Die Koeffizienten von sys1 sind in absteigenden Potenzen von z geordnet.

tf wechselt basierend auf dem Wert der Eigenschaft 'Variable' die Konvention. Da sys2 das inverse Transferfunktionsmodell von sys1 ist, geben Sie ‚z^-1‘ als ‚Variable‘ an und verwenden dieselben Koeffizienten für Zähler und Nenner.

sys2 = tf(numerator,denominator,ts,'Variable','z^-1')

sys2 =
 
           1
  -------------------
  1 + 2 z^-1 + 3 z^-2
 
Sample time: 0.1 seconds
Discrete-time transfer function.
Model Properties

Die Koeffizienten von sys2 sind jetzt in aufsteigenden Potenzen von z^-1 geordnet.

Basierend auf verschiedenen Konventionen können Sie die Polynomordnung in Transferfunktionsmodellen mithilfe der Eigenschaft 'Variable' festlegen.

Optimierbarer Tiefpassfilter

In diesem Beispiel werden Sie einen Tiefpassfilter mit einem optimierbaren Parameter a erstellen:

$$F=\frac{a}{s+a}$$

Da die Koeffizienten von Zähler und Nenner eines tunableTF-Blocks unabhängig sind, können Sie tunableTF nicht zur Darstellung von F verwenden. Konstruieren Sie F stattdessen mit dem optimierbaren realen Parameterobjekt realp.

Erstellen Sie einen optimierbaren realen Parameter mit einem Anfangswert von 10.

a = realp('a',10)

a = 
       Name: 'a'
      Value: 10
    Minimum: -Inf
    Maximum: Inf
       Free: 1

Real scalar parameter.

Verwenden Sie tf, um den abstimmbaren Tiefpassfilter F zu erstellen.

numerator = a;
denominator = [1,a];
F = tf(numerator,denominator)

Generalized continuous-time state-space model with 1 outputs, 1 inputs, 1 states, and the following blocks:
  a: Scalar parameter, 2 occurrences.
Model Properties

Type "ss(F)" to see the current value and "F.Blocks" to interact with the blocks.

F ist ein genss-Objekt, das den optimierbaren Parameter a in seiner Blocks-Eigenschaft hat. Sie können F mit anderen optimierbaren oder numerischen Modellen verbinden, um komplexere Steuersystemmodelle zu erstellen. Ein Beispiel hierzu finden Sie unter Control System with Tunable Components.

MIMO-Transferfunktionsmodell mit statischer Verstärkung

In diesem Beispiel werden Sie ein MIMO-Transferfunktionsmodell mit statischer Verstärkung erstellen.

Betrachten Sie die folgende statische Verstärkungsmatrix m mit zwei Eingängen und zwei Ausgängen:

$$m=\left[\begin{array}{cc}2& 4\\ 3& 5\end{array}\right]$$

Geben Sie die Verstärkungsmatrix an und erstellen Sie das Transferfunktionsmodell mit statischer Verstärkung.

m = [2,4;...
    3,5];
sys1 = tf(m)

sys1 =
 
  From input 1 to output...
   1:  2
 
   2:  3
 
  From input 2 to output...
   1:  4
 
   2:  5
 
Static gain.
Model Properties

Sie können das oben erhaltene Transferfunktionsmodell sys1 mit statischer Verstärkung verwenden, um es mit einem anderen Transferfunktionsmodell zu kaskadieren.

In diesem Beispiel erstellen Sie ein weiteres diskretes Transferfunktionsmodell mit zwei Eingängen und zwei Ausgängen und verwenden die series-Funktion, um die beiden Modelle zu verbinden.

numerators = {1,[1,0];[-1,2],3};
denominator = [1,0.3];
ts = 0.2;
sys2 = tf(numerators,denominator,ts)

sys2 =
 
  From input 1 to output...
          1
   1:  -------
       z + 0.3
 
       -z + 2
   2:  -------
       z + 0.3
 
  From input 2 to output...
          z
   1:  -------
       z + 0.3
 
          3
   2:  -------
       z + 0.3
 
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties

sys = series(sys1,sys2)

sys =
 
  From input 1 to output...
       3 z^2 + 2.9 z + 0.6
   1:  -------------------
       z^2 + 0.6 z + 0.09
 
       -2 z^2 + 12.4 z + 3.9
   2:  ---------------------
        z^2 + 0.6 z + 0.09
 
  From input 2 to output...
       5 z^2 + 5.5 z + 1.2
   1:  -------------------
       z^2 + 0.6 z + 0.09
 
       -4 z^2 + 21.8 z + 6.9
   2:  ---------------------
        z^2 + 0.6 z + 0.09
 
Sample time: 0.2 seconds
Discrete-time transfer function.
Model Properties

Berechnen einer verkürzten Transferfunktion zur Annäherung eines schwach besetzten Modells

Seit R2025a

Dieses Beispiel zeigt, wie Sie ein verkürztes Transferfunktionsmodell eines schwach besetzten Zustandsraummodells erhalten. In diesem Beispiel wird ein schwach besetztes Modell verwendet, das durch Linearisierung eines thermischen Modells der Wärmeverteilung in einem kreiszylindrischen Stab gewonnen wurde.

Laden Sie die Modelldaten.

load cylindricalRod.mat
sys = sparss(A,B,C,D,E);
w = logspace(-7,-1,20);
size(sys)

Sparse state-space model with 3 outputs, 1 inputs, and 7522 states.

Analysieren Sie den Frequenzgang des Modells.

sigmaplot(sys,w)

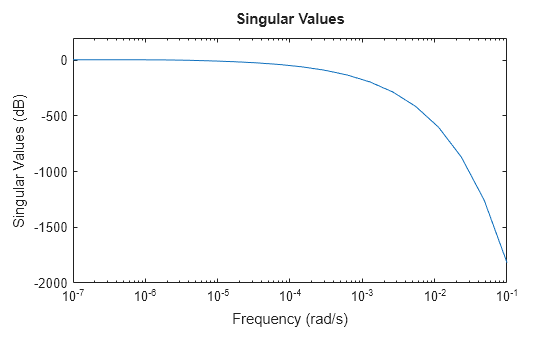
Um eine verkürzte Annäherung zu erhalten, verwenden Sie tf und geben Sie das Frequenzband des Fokus an. Bei diesem Modell können Sie einen Frequenzbereich von 0 rad/s bis 0.01 rad/s verwenden, um die Näherung niedriger Ordnung zu erhalten.

tsys = tf(sys,Focus=[0 1e-2],Display="off");

Vergleichen Sie den Frequenzgang.

sigmaplot(sys,tsys,w)

Dieses thermische Modell fällt jenseits von 0.001 rad/s sehr steil ab. Standardmäßig bietet das mit tf erhaltene reduzierte Modell keine gute Übereinstimmung mit diesem Abfall. Um dies abzumildern, können Sie das Argument RollOff von tf verwenden und einen minimalen Abfall-Wert jenseits des fokussierten Frequenzbandes angeben. Geben Sie für die Abfallrate einen Wert von -45 an, was einer Rate von mindestens -900 dB/Dekade entspricht.

tsys2 = tf(sys,Focus=[0 1e-2],RollOff=-45,Display="off");
sigmaplot(sys,tsys2,w)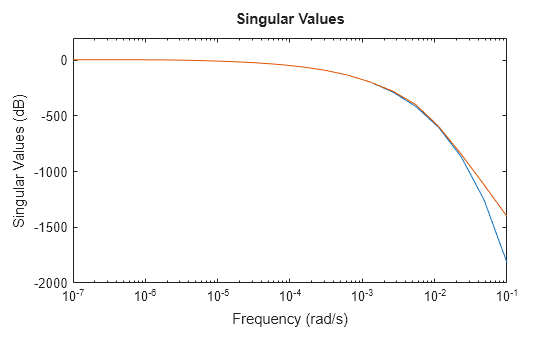

Das reduzierte Modell liefert nun eine viel bessere Annäherung an den Abfall-Wert. In diesem Beispiel führt die Anpassung der Abfallrate mit tf jedoch dazu, dass die Nullstellen und Polstellen erneut berechnet werden müssen. Dies kann bei großen Modellen sehr rechenintensiv sein. Als Alternative können Sie die Methode der Nullpolabschneidung von reducespec verwenden und den Abfall ohne zusätzliche Berechnungskosten anpassen, nachdem die Software die Polstellen und Nullstellen berechnet hat. Ein Beispiel hierzu finden Sie unter Zero-Pole Truncation of Thermal Model.

Beschränkungen

• Transferfunktionsmodelle sind für numerische Berechnungen schlecht geeignet. Konvertieren Sie die erstellten Modelle in die Zustandsraumform, bevor Sie sie mit anderen Modellen kombinieren oder Modelltransformationen durchführen. Sie können die resultierenden Modelle dann zu Prüfzwecken wieder in die Transferfunktionsform konvertieren.

• Ein identifiziertes nichtlineares Modell kann nicht mit tf direkt in ein Transferfunktionsmodell umgewandelt werden. So erhalten Sie ein Transferfunktionsmodell:

  1. Konvertieren Sie das identifizierte nichtlineare Modell mit linapp (System Identification Toolbox), idnlarx/linearize (System Identification Toolbox) oder idnlhw/linearize (System Identification Toolbox) in ein identifiziertes LTI-Modell.

  2. Konvertieren Sie das resultierende Modell dann mit tf in ein Transferfunktionsmodell.

Algorithmen

Zur Konvertierung schwach besetzter Modelle verwendet tf den Krylov-Schur-Algorithmus [1] für inverse Potenziteration, um Polstellen und Nullstellen im angegebenen Frequenzband zu berechnen.

Referenzen

[1] Stewart, G. W. “A Krylov--Schur Algorithm for Large Eigenproblems.” SIAM Journal on Matrix Analysis and Applications 23, no. 3 (January 2002): 601–14. https://doi.org/10.1137/S0895479800371529.

Versionsverlauf

Eingeführt vor R2006a

R2025a: Berechnen einer verkürzten Transferfunktionsannäherung von schwach besetzten Modellen

Sie können nun mit tf schwach besetzte Zustandsraummodelle konvertieren und eine verkürzte Annäherung der Transferfunktion erhalten. tf berechnet eine Teilmenge der Nullstellen und Polstellen von schwach besetzten Modellen, typischerweise in einem bestimmten niederfrequenten Band [0 f_max]. Dies kann zu einer besseren Annäherung an niedrige Frequenzen führen als die Reduzierung der Modellordnung durch modale Trunkierung – allerdings auf Kosten eines höheren Rechenaufwands. tf bietet auch eine direkte Kontrolle über die Abfallrate über die Frequenz f_max hinaus. Verwenden Sie die neue Syntax tsys = tf(sparseSys,Name=Value), um eine Annäherung zu erhalten, die auf bestimmten Optionen basiert, wie z. B. dem Frequenzbereich des Fokus. Ein Beispiel hierzu finden Sie unter Berechnen einer verkürzten Transferfunktion zur Annäherung eines schwach besetzten Modells.

Siehe auch

filt | frd | get | set | ss | tfdata | zpk | genss | realp | genmat | tunableTF

Themen

• What Are Model Objects?
• Transferfunktionen
• Discrete-Time Numeric Models
• MIMO-Transferfunktionen
• Using the Right Model Representation
• FEEDBACK zum Schließen von Rückkopplungsschleifen verwenden

Externe Websites

• Transferfunktionsanalyse dynamischer Systeme (MathWorks Unterrichtsmaterialien)