kalman
Design Kalman filter for state estimation
Syntax
Description
[
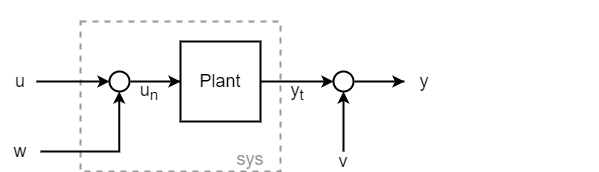
creates a Kalman filter given the plant model kalmf,L,P] = kalman(sys,Q,R,N)sys and the noise
covariance data Q, R, and N.
The function computes a Kalman filter for use in a Kalman estimator with the configuration
shown in the following diagram.

You construct the model sys with known inputs u
and white process noise inputs w, such that w consists
of the last Nw inputs to sys.
The "true" plant output yt consists of all outputs
of sys. You also provide the noise covariance data
Q, R, and N. The returned
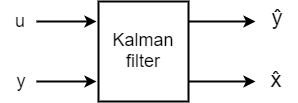
Kalman filter kalmf is a state-space model that takes the known inputs
u and the noisy measurements y and produces an
estimate of the true plant output and an estimate of the plant states. kalman also returns the Kalman
gains L and the steady-state error covariance matrix
P.
[
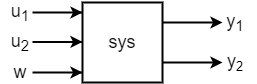
computes a Kalman filter when one or both of the following conditions exist.kalmf,L,P] = kalman(sys,Q,R,N,sensors,known)
Not all outputs of
sysare measured.The disturbance inputs w are not the last inputs of
sys.
The index vector sensors specifies which outputs of
sys are measured. These outputs make up y. The
index vector known specifies which inputs are known (deterministic).
The known inputs make up u. The kalman command takes
the remaining inputs of sys to be the stochastic inputs
w.
[
specifies the estimator type for a discrete-time kalmf,L,P,Mx,Z,My] = kalman(___,type)sys.
type = 'current'— Compute output estimates and state estimates using all available measurements up to .type = 'delayed'— Compute output estimates and state estimates using measurements only up to . The delayed estimator is easier to implement inside control loops.
You can use the type input argument with any of the
previous input argument combinations.
Examples
Input Arguments
Output Arguments
Limitations
The plant and noise data must satisfy:
(C,A) is detectable, where:
and , where
has no uncontrollable mode on the imaginary axis in continuous time, or on the unit circle in discrete time.
Algorithms
Version History
Introduced before R2006a