feedback

Feedback-Verbindung mehrere Modelle

Syntax

sys = feedback(sys1,sys2)

sys = feedback(sys1,sys2,feedin,feedout)

sys = feedback(sys1,sys2,'name')

sys = feedback(___,sign)

Beschreibung

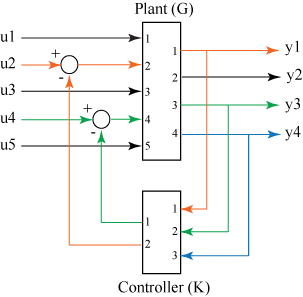
sys = feedback(sys1,sys2) gibt ein Modellobjekt sys für eine negative Feedback-Schaltung zwischen den Modellobjekten sys1,sys2 aus.

In dieser Abbildung weist das geschlossene Modell sys u als Eingangsvektor und y als Ausgangsvektor auf. Beide Modelle sys1 und sys2 müssen entweder kontinuierlich oder diskret sein und identische Abtastzeiten aufweisen.

sys = feedback(sys1,sys2,feedin,feedout) berechnet ein geschlossenes Modell sys mithilfe der Eingangs- und Ausgangsverbindungen mithilfe feedin und feedout. Verwenden Sie diese Syntax, wenn Sie nur eine Untermenge der verfügbaren E/As von MIMO-Systemen verbinden möchten.

sys = feedback(sys1,sys2,'name') berechnet ein geschlossenes Modell sys mit Feedback-Verbindungen, die von den jeweiligen E/A-Namen der MIMO-Modelle sys1 und sys2 festgelegt werden. Verwenden Sie die Kennzeichnung 'name' nur, wenn alle erforderlichen E/As der MIMO-Systeme korrekt benannt wurden.

sys = feedback(___,sign) gibt ein Modellobjekt sys für die Feedbackschleife aus; der Typ des Feedbacks wird durch sign angegeben. Standardmäßig nimmt feedback negatives Feedback an und ist zu feedback(sys1,sys2,-1) äquivalent. Um das geschlossene System mit positivem Feedback zu berechnen, verwenden Sie sign = +1.

Beispiele

Regelstrecke und Regler mit Einheitsfeedback

pendulumModelAndController.mat enthält ein invertiertes SISO-Pendel-Transferfunktionsmodell G und den zugehörigen PID-Regler C.

Laden Sie das invertierte Pendelmodell und das Reglermodell in den Workspace.

load('pendulumModelAndController','G','C');
size(G)

Transfer function with 1 outputs and 1 inputs.

size(C)

PID controller with 1 output and 1 input.

Zum Erstellen dieser Schleifenstruktur schalten Sie die Regler- und Anlagenmodelle in Reihe, um sys1 zu erstellen, und setzen Sie sys2 auf 1, da es sich um das Einheitsfeedback handelt. Standardmäßig wendet die Funktion ein negatives Feedback an, aber Sie können mit dem optionalen Argument sign die Art des Feedbacks festlegen. In diesem Beispiel können Sie das Argument sign entweder weglassen oder es auf -1 setzen, um ein negatives Feedback zu erhalten.

sys1 = G*C;
sys2 = 1;
sign = -1;

Verwenden Sie feedback, um die negative Feedbackschleife mit G und C zu erstellen.

sys = feedback(sys1,sys2,sign)

sys =
 
         1.307e-06 s^3 + 3.136e-05 s^2 + 5.227e-06 s
  ---------------------------------------------------------
  2.3e-06 s^4 + 1.725e-06 s^3 - 4.035e-05 s^2 - 5.018e-06 s
 
Continuous-time transfer function.
Model Properties

sys ist die resultierende zeitkontinuierliche Transferfunktion des geschlossenen Regelkreises, die mit negativem Feedback erhalten wird.

Regelstrecke mit Regler in negativem Feedbackpfad

Betrachten Sie in diesem Beispiel zwei Transferfunktionen, die eine Regelstrecke G und einen Regler C beschreiben.

$$G(s)=\frac{2s^2+5s+1}{s^2+2s+3}C(s)=\frac{5(s+2)}{s+10}$$

Erstellen Sie die Regelstrecke und die Regler-Transferfunktionen.

G = tf([2 5 1],[1 2 3],'inputname',"torque",'outputname',"velocity");
C = tf([5,10],[1,10]); 

Verwenden Sie feedback, um die negative Feedbackschleife mit G und C zu erstellen.

sys = feedback(G,C,-1)

sys =
 
  From input "torque" to output "velocity":
  2 s^3 + 25 s^2 + 51 s + 10
  ---------------------------
  11 s^3 + 57 s^2 + 78 s + 40
 
Continuous-time transfer function.
Model Properties

sys ist die resultierende geschlossene Transferfunktion, die mithilfe von negativem Feedback mit dem Eingang torque und dem Ausgang velocity erzeugt wird.

Positive Feedbackschleife mit Regelstrecke und Regler

Betrachten Sie in diesem Beispiel zwei Transferfunktionen, die eine Regelstrecke G und einen Regler C beschreiben.

$$G(s)=\frac{2s^2+5s+1}{s^2+2s+3}C(s)=\frac{5(s+2)}{s+10}$$

Erstellen Sie die Regelstrecke und die Regler-Transferfunktionen.

G = tf([2 5 1],[1 2 3],'inputname',"torque",'outputname',"velocity");
C = tf([5,10],[1,10]); 

Verwenden Sie feedback, um mithilfe von G und C die positive Feedbackschleife zu erstellen.

sys = feedback(G,C,+1)

sys =
 
  From input "torque" to output "velocity":
  -2 s^3 - 25 s^2 - 51 s - 10
  ---------------------------
  9 s^3 + 33 s^2 + 32 s - 20
 
Continuous-time transfer function.
Model Properties

sys ist die resultierende geschlossene Transferfunktion, die mithilfe von positivem Feedback mit dem Eingang torque und dem Ausgang velocity erzeugt wird.

Negative Feedbackschleife mit MIMO-Systemen

Betrachten Sie auf Grundlage der Abbildung unten die Verbindung von zwei MIMO-Transferfunktionen mit zwei Eingängen und zwei Ausgängen in einer negativen Feedbackschleife.

Erstellen Sie für dieses Beispiel mithilfe von rss zwei zufällige kontinuierliche Zustandsraummodelle.

G = rss(4,2,2);
C = rss(2,2,2);
size(G)

State-space model with 2 outputs, 2 inputs, and 4 states.

size(C)

State-space model with 2 outputs, 2 inputs, and 2 states.

Verwenden Sie feedback, um gemäß der Abbildung oben die zwei Zustandsraummodelle in einer negativen Feedbackschleife zu verbinden.

sys = feedback(G,C,-1);
size(sys)

State-space model with 2 outputs, 2 inputs, and 6 states.

Das resultierende Zustandsraummodell sys ist ein Modell mit zwei Eingängen und zwei Ausgängen mit 6 Zuständen. Die negative Feedbackschleife wird so geschlossen, dass

• Der erste Ausgang von G mit dem ersten Eingang von C verbunden ist

• Der zweite Ausgang von G mit dem zweiten Eingang von C verbunden ist

Feedbackschleife auf Grundlage von E/A-Namen

mimoPlantAndController.mat umfasst ein Transferfunktions-Regelstreckenmodell G mit zwei Eingängen und zwei Ausgängen und ein Transferfunktions-Reglermodell C mit zwei Eingängen und zwei Ausgängen, die folgendermaßen verbunden werden:

Laden Sie zunächst die Regelstrecke und die Reglermodelle in den Workspace.

load('mimoPlantAndController.mat','G','C');
size(G)

Transfer function with 2 outputs and 2 inputs.

size(C)

Transfer function with 2 outputs and 2 inputs.

Standardmäßig verbindet feedback den ersten Ausgang von G mit dem ersten Eingang von C und den zweiten Ausgang von G mit dem zweiten Eingang von C. Um die Regelstrecke und den Regler gemäß der Abbildung zu verbinden und korrekte Verbindungen zu gewährleisten, benennen Sie die E/As der zwei Systeme.

G.InputName 

ans = 2×1 cell
    {'torque'}
    {'angle' }

G.OutputName

ans = 2×1 cell
    {'velocity'}
    {'force'   }

C.InputName

ans = 2×1 cell
    {'force'   }
    {'velocity'}

C.OutputName

ans = 2×1 cell
    {'angle' }
    {'torque'}

Verwenden Sie daraufhin die Kennzeichnung 'name' und den Befehl feedback, um die Verbindungen gemäß der E/A-Namen herzustellen.

sys = feedback(G,C,'name');

Die resultierende geschlossene negative Feedback-Transferfunktion sys verfügt über die Feedback-Verbindungen in der erforderlichen Reihenfolge.

Angeben von Eingangs- und Ausgangsverbindungen in einer Feedbackschleife

Betrachten Sie eine Zustandsraum-Regelstrecke G mit fünf Eingängen und vier Ausgängen und einen Zustandsraum-Feedbackregler K mit drei Eingängen und zwei Ausgängen. Die Ausgänge 1, 3 und 4 der Regelstrecke G müssen mit den Eingängen des Reglers K verbunden sein; die Regler-Ausgänge müssen mit den Eingängen 2 und 4 der Regelstrecke verbunden sein.

Generieren Sie für dieses Beispiel mithilfe von rss randomisierte zeitkontinuierliche Zustandsraummodelle für G und K.

G = rss(3,4,5);
K = rss(3,2,3);

Definieren Sie die Vektoren feedout und feedin auf Grundlage der Eingänge und Ausgänge, die in der Feedbackschleife verbunden werden sollen.

feedin = [2 4];
feedout = [1 3 4];
sys = feedback(G,K,feedin,feedout,-1);
size(sys)

State-space model with 4 outputs, 5 inputs, and 6 states.

sys ist das resultierende geschlossene Zustandsraummodell, das durch Verbindung der festgelegten Eingänge und Ausgänge von G und K erstellt wird.

Eingabeargumente

sys1,sys2 — In einer Feedbackschleife zu verbindende Systeme

dynamische Systemmodelle

In einer Feedbackschleife zu verbindende Systeme, festgelegt als dynamische Systemmodelle. Zu den dynamischen Systemen, die Sie verwenden können, zählen:

• Zeitkontinuierliche oder zeitdiskrete numerische LTI-Modelle, wie tf-, zpk-, pid-, pidstd- oder ss-Modelle.

• Frequenzantwort-Modelle wie frd oder genfrd.

• Verallgemeinerte oder unsichere LTI-Modelle wie z. B. genss- oder uss (Robust Control Toolbox)-Modelle. (Für die Verwendung unsicherer Modelle ist die Software Robust Control Toolbox™ erforderlich.)

  Die resultierende Feedbackschleife geht von folgenden Annahmen aus:

  • aktuelle Werte der optimierbaren Komponenten für optimierbare Regelungsentwurf-Blöcke

  • nominale Modellwerte für unsichere Regelungsentwurf-Blöcke

Weitere Informationen finden Sie unter dynamische Systemmodelle.

Wenn es sich bei sys1 und sys2 um zwei verschiedene Modelltypen handelt, verwendet feedback Vorrangregeln, um das resultierende Modell sys zu ermitteln. Werden beispielsweise ein Zustandsraummodell und ein Transfermodell in einer Feedbackschleife verbunden, ist das resultierende System ein Zustandsraummodell auf Grundlage der Vorrangregeln. Weitere Informationen finden Sie unter Rules That Determine Model Type.

feedin — Untermenge der zu verwendenden Eingänge

Vektor

Untermenge der zu verwendenden Eingänge, angegeben als Vektor.

In dieser Abbildung enthält feedin Indizes des Eingangsvektors der MIMO-Regelstrecke P und legt fest, welche Untermenge der Eingänge u an der Feedbackschleife beteiligt sind. Das resultierende Modell sys weist dieselben Eingänge wie G auf, und die Reihenfolge der Eingänge wird bewahrt.

Ein Beispiel hierzu finden Sie unter Angeben von Eingangs- und Ausgangsverbindungen in einer Feedbackschleife.

feedout — Untermenge der zu verwendenden Ausgänge

Vektor

Untermenge der zu verwendenden Ausgänge, angegeben als Vektor.

feedout legt fest, welche Ausgänge der MIMO-Regelstrecke G für das Feedback verwendet werden. Das resultierende Modell sys weist dieselben Ausgänge wie G auf, und die Reihenfolge der Ausgänge wird bewahrt.

Ein Beispiel hierzu finden Sie unter Angeben von Eingangs- und Ausgangsverbindungen in einer Feedbackschleife.

sign — Feedbacktyp

-1 (Standardeinstellung) | +1

Feedbacktyp, angegeben als -1 für negatives Feedback oder +1 für positives Feedback. feedback geht standardmäßig von negativem Feedback aus.

Ausgangsargumente

sys — Geschlossener Regelkreis

dynamisches Systemmodell

Geschlossener Regelkreis, ausgegeben als dynamisches SISO- oder MIMO-Systemmodell. sys kann je nach Vorrangregeln vom folgenden Typ sein:

• Zeitkontinuierliche oder zeitdiskrete numerische LTI-Modelle, wie tf-, zpk-, ss-, pid- oder pidstd-Modelle.

• Verallgemeinerte oder unsichere LTI-Modelle wie z. B. genss- oder uss (Robust Control Toolbox)-Modelle. (Für die Verwendung unsicherer Modelle ist die Software Robust Control Toolbox erforderlich.)

Wenn es sich bei sys1 und sys2 um zwei verschiedene Modelltypen handelt, verwendet feedback Vorrangregeln, um das resultierende Modell sys zu ermitteln. Werden beispielsweise ein Zustandsraummodell und ein Transfermodell in einer Feedbackschleife verbunden, ist das resultierende System ein Zustandsraummodell auf Grundlage der Vorrangregeln, wie in Rules That Determine Model Type beschrieben.

Beschränkungen

• Die Feedback-Verbindung darf keine algebraischen Schleifen aufweisen. Wenn beispielsweise D₁ und D₂ die Feedthrough-Matrizen von sys1 und sys2 sind, ist diese Bedingung äquivalent zu:

  • I + D₁D₂ nichtsingulär bei Verwendung von negativem Feedback

  • I − D₁D₂ nichtsingulär bei Verwendung von positivem Feedback

Tipps

• Verwenden Sie für komplizierte Feedback-Strukturen append und connect.

Versionsverlauf

Eingeführt vor R2006a

Siehe auch

append | connect | series | lft | sumblk | parallel

Themen

• Rules That Determine Model Type
• MIMO Feedback Loop
• FEEDBACK zum Schließen von Rückkopplungsschleifen verwenden