step
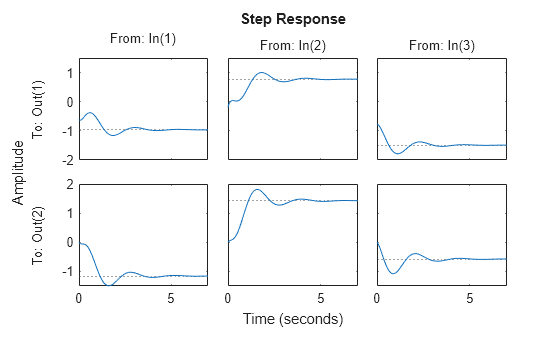
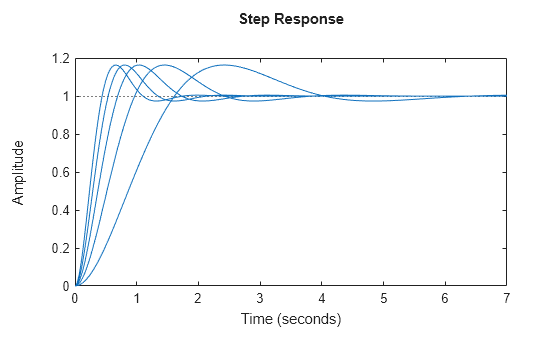
Sprungantwort eines dynamischen Systems
Syntax
Beschreibung
step berechnet die Sprungantwort auf eine sprunghafte Änderung des Eingangswertes von U auf U + dU nach td Zeiteinheiten.
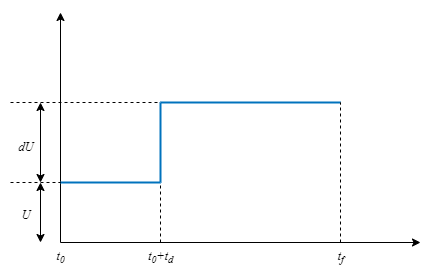
Dabei gilt:
t0 ist die Startzeit der Simulation.
td ist die Sprungverzögerung.
U ist der Eingangsgrundwert oder Vorgabewert.
dU ist die Sprungamplitude.
Standardmäßig wendet die Funktion den Sprung bei t0 = 0, U = 0, dU = 1 und td = 0 an. Sie können diese Werte jedoch mit RespConfig konfigurieren. Sie können auch den Anfangszustand x(t0) angeben. Wenn Sie den Anfangszustand nicht angeben, geht step davon aus, dass sich das System anfangs im Ruhezustand befindet und der Eingangspegel U ist.
[ simuliert die Antwort für die Zeitschritte, die durch y,tOut] = step(sys,t)t angegeben sind. Zum Definieren der Zeitschritte können Sie folgendes angeben:
Die endgültige Simulationszeit unter Verwendung eines skalaren Werts.
Die Anfangs- und Endzeit der Simulation unter Verwendung eines Vektors mit zwei Elementen. (seit R2023b)
Alle Zeitschritte unter Verwendung eines Vektors.
[ gibt zusätzliche Optionen für die Berechnung der Sprungantwort an, z. B. die Sprungamplitude oder den Eingangsoffset. Verwenden Sie y,tOut] = step(___,config)RespConfig zum Erstellen von config.
step(___) plottet die Sprungantwort von sys mit Standard-Darstellungsoptionen für alle vorherigen Kombinationen von Eingangsargumenten. Weitere Informationen zu den Anpassungsmöglichkeiten von Diagrammen finden Sie unter stepplot.
Um Antworten für mehrere dynamische Systeme auf einem Diagramm zu plotten, können Sie
sysals kommagetrennte Modellliste angeben.step(sys1,sys2,sys3)plottet beispielsweise die Antworten für drei Modelle auf demselben Diagramm.Um eine Farbe, einen Linienstil und eine Markierung für jedes System im Diagramm darzustellen, geben Sie für jedes System einen Wert
LineSpecan. Mithilfe vonstep(sys1,LineSpec1,sys2,LineSpec2)können Sie beispielsweise zwei Modelle zeichnen und deren Diagrammstil festlegen. Weitere Informationen zum Festlegen einesLineSpec-Werts finden Sie unterstepplot.
Beispiele
Plotten Sie die Sprungantwort eines zeitkontinuierlichen Systems, das durch die folgende Transferfunktion dargestellt wird.
Erstellen Sie für dieses Beispiel ein tf-Modell, das die Transferfunktion darstellt. In ähnlicher Weise können Sie die Sprungantwort anderer dynamischer Systemmodelle plotten, wie z. B. Nullpolverstärkungsmodelle (zpk) oder Zustandsraummodelle (ss).
sys = tf(4,[1 2 10]);
Plotten Sie die Sprungantwort.
step(sys)
Das step-Diagramm enthält automatisch eine gepunktete horizontale Linie, die das stationäre Verhalten anzeigt. In einem MATLAB®-Abbildungsfenster können Sie auf das Diagramm rechtsklicken, um weitere Sprungantwortcharakteristiken wie Spitzenwert und Einschwingzeit anzuzeigen. Weitere Informationen zu diesen Merkmalen finden Sie unter stepinfo.
Plotten Sie die Sprungantwort eines zeitdiskreten Systems. Das System hat eine Abtastzeit von 0,2 s und wird durch die folgenden Zustandsraummatrizen dargestellt.
A = [1.6 -0.7;
1 0];
B = [0.5; 0];
C = [0.1 0.1];
D = 0;Erstellen Sie das Zustandsraummodell und plotten Sie seine Sprungantwort.
sys = ss(A,B,C,D,0.2); step(sys)
Die Sprungantwort spiegelt die Diskretisierung des Modells wider und zeigt die alle 0,2 Sekunden berechnete Antwort.
Untersuchen Sie die Sprungantwort der folgenden Transferfunktion.
sys = zpk(-1,[-0.2+3j,-0.2-3j],1) * tf([1 1],[1 0.05])
sys =
(s+1)^2
----------------------------
(s+0.05) (s^2 + 0.4s + 9.04)
Continuous-time zero/pole/gain model.
Model Properties
step(sys)
Standardmäßig wählt step einen Endzeitpunkt, der den stationären Zustand anzeigt, zu dem die Antwort tendiert. Dieses System hat jedoch schnelle Transienten, die auf dieser Zeitskala verdeckt sind. Um einen genaueren Blick auf das Einschwingverhalten zu erhalten, begrenzen Sie das Sprungdiagramm auf t = 15 s.
step(sys,15)
Sie können auch die genauen Zeitpunkte angeben, zu denen Sie die Sprungantwort untersuchen wollen, sofern sie durch ein konstantes Intervall getrennt sind. Untersuchen Sie zum Beispiel die Antwort vom Ende des Einschwingvorgangs bis zum Erreichen des stationären Zustands des Systems.
t = 20:0.2:120; step(sys,t)
Auch wenn dieses Diagramm bei t = 20 beginnt wendet step immer die Schritteingabe bei t = 0 an.
Betrachten Sie das folgende Zustandsraummodell zweiter Ordnung:
A = [-0.5572,-0.7814;0.7814,0]; B = [1,-1;0,2]; C = [1.9691,6.4493]; sys = ss(A,B,C,0);
Dieses Modell hat zwei Eingänge und einen Ausgang, es hat also zwei Kanäle: vom ersten Eingang zum Ausgang und vom zweiten Eingang zum Ausgang. Jeder Kanal hat seine eigene Sprungantwort.
Wenn Sie step verwenden, werden die Antworten aller Kanäle berechnet.
step(sys)
Das linke Diagramm zeigt die Sprungantwort des ersten Eingangskanals, das rechte Diagramm die Sprungantwort des zweiten Eingangskanals. Wann immer Sie mit step die Antworten eines MIMO-Modells plotten, wird ein Array von Diagrammen erzeugt, die alle E/A-Kanäle des Modells darstellen. Erstellen Sie zum Beispiel ein zufälliges Zustandsraummodell mit fünf Zuständen, drei Eingängen und zwei Ausgängen und plotten Sie seine Sprungantwort.
sys = rss(5,2,3); step(sys)
In einem MATLAB-Abbildungsfenster können Sie das Diagramm auf eine Teilmenge von Kanälen beschränken, indem Sie auf das Diagramm rechtsklicken und I/O Selector wählen.
step ermöglicht es Ihnen, die Antworten mehrerer dynamischer Systeme auf derselben Achse darzustellen. Vergleichen Sie zum Beispiel das Regelverhalten eines Systems mit einem PI-Regler und einem PID-Regler. Erstellen Sie eine Transferfunktion des Systems und optimieren Sie die Regler.
H = tf(4,[1 2 10]); C1 = pidtune(H,'PI'); C2 = pidtune(H,'PID');
Bilden Sie die geschlossenen Regelkreise und plotten Sie deren Sprungantworten.
sys1 = feedback(H*C1,1); sys2 = feedback(H*C2,1); step(sys1,sys2) legend('PI','PID','Location','SouthEast')
Standardmäßig wählt step unterschiedliche Farben für jedes System aus, das Sie plotten. Sie können Farben und Linienstile mit dem Eingabeargument LineSpec angeben.
step(sys1,'r--',sys2,'b') legend('PI','PID','Location','SouthEast')
Das erste LineSpec, 'r--', legt eine gestrichelte rote Linie für die Antwort mit dem PI-Regler fest. Das zweite LineSpec, 'b', legt eine durchgezogene blaue Linie für die Antwort mit dem PID-Regler fest. Die Legende spiegelt die angegebenen Farben und Linienstile wider. Weitere Informationen zu den Anpassungsmöglichkeiten von Diagrammen finden Sie unter stepplot.
Das Beispiel „Vergleichen der Antworten mehrerer Systeme“ zeigt, wie die Antworten mehrerer individueller Systeme auf einer einzigen Achse geplottet werden können. Wenn Sie mehrere dynamische Systeme in einem Modellarray angeordnet haben, plottet step alle ihre Antworten auf einmal.
Erstellen Sie ein Modellarray. Verwenden Sie für dieses Beispiel ein eindimensionales Array von Transferfunktionen zweiter Ordnung mit unterschiedlichen Eigenfrequenzen. Weisen Sie zunächst den Speicher für das Modellarray zu. Der folgende Befehl erstellt eine 1-mal-5-Reihe von SISO-Transferfunktionen mit Null-Verstärkung. Die ersten beiden Dimensionen stellen die Ausgänge und Eingänge des Modells dar. Die übrigen Dimensionen sind die Arraydimensionen.
sys = tf(zeros(1,1,1,5));
Füllen Sie das Array auf.
w0 = 1.5:1:5.5; % natural frequencies zeta = 0.5; % damping constant for i = 1:length(w0) sys(:,:,1,i) = tf(w0(i)^2,[1 2*zeta*w0(i) w0(i)^2]); end
(Weitere Informationen über Modellarrays und deren Erstellung finden Sie unter Model Arrays) Plotten Sie die Sprungantworten aller Modelle im Array.
step(sys)
step verwendet den gleichen Linienstil für die Antworten aller Einträge im Array. Eine Möglichkeit, zwischen den Einträgen zu unterscheiden, ist die Verwendung der SamplingGrid-Eigenschaft dynamischer Systemmodelle, um jedem Eintrag im Array den entsprechenden w0-Wert zuzuordnen.
sys.SamplingGrid = struct('frequency',w0);Wenn Sie nun die Antworten in einem MATLAB-Abbildungsfenster plotten, können Sie auf eine Kurve klicken, um zu sehen, welchem Frequenzwert sie entspricht.
Wenn Sie ihr ein Ausgangs-Argument angeben, gibt die Funktion step ein Array mit Antwortdaten zurück. Bei einem SISO-System werden die Antwortdaten als Spaltenvektor zurückgegeben, dessen Länge der Anzahl der Zeitpunkte entspricht, zu denen die Antwort abgetastet wird. Sie können den Vektor t der Zeitpunkte angeben oder zulassen, dass step auf der Grundlage der Systemdynamik Zeitpunkte für Sie auswählt. Extrahieren Sie zum Beispiel die Sprungantwort eines SISO-Systems zu 101 Zeitpunkten zwischen t = 0 und t = 5 s.
sys = tf(4,[1 2 10]); t = 0:0.05:5; y = step(sys,t); size(y)
ans = 1×2
101 1
Bei einem MIMO-System werden die Antwortdaten in einem Array der Dimensionen N-mal-Ny-mal-Nu zurückgegeben, wobei Ny und Nu die Anzahl der Ausgänge und Eingänge des dynamischen Systems sind. Betrachten Sie zum Beispiel das folgende Zustandsraummodell, das ein System mit zwei Eingängen und einem Ausgang darstellt.
A = [-0.5572,-0.7814;0.7814,0]; B = [1,-1;0,2]; C = [1.9691,6.4493]; sys = ss(A,B,C,0);
Extrahieren Sie die Sprungantwort dieses Systems zu 200 Zeitpunkten zwischen t = 0 und t = 20 s.
t = linspace(0,20,200); y = step(sys,t); size(y)
ans = 1×3
200 1 2
y(:,i,j) ist ein Spaltenvektor, der die Sprungantwort des j-ten Eingangs zum i-ten Ausgang zu den Zeitpunkten t enthält. Extrahieren Sie zum Beispiel die Sprungantwort vom zweiten Eingang zum Ausgang.
y12 = y(:,1,2); plot(t,y12)
Erstellen Sie eine Rückkopplungsschleife mit Verzögerung und zeichnen Sie deren Sprungantwort auf.
s = tf('s');
G = exp(-s) * (0.8*s^2+s+2)/(s^2+s);
sys = feedback(ss(G),1);
step(sys)
Die angezeigte Sprungantwort des Systems ist chaotisch. Die Sprungantwort von Systemen mit internen Verzögerungen kann ein merkwürdiges Verhalten aufweisen, z. B. wiederkehrende Sprünge. Ein solches Verhalten ist eine Eigenschaft des Systems und keine Softwareanomalie.
Standardmäßig wendet step ein Eingangssignal an, das bei t = 0 von 0 auf 1 wechselt. Verwenden Sie RespConfig, um die Amplitude und den Vorgabewert anzupassen. Berechnen Sie z. B. die Reaktion eines SISO-Zustandsraummodells auf ein Signal, das bei t = 0 von 1 auf –1 wechselt.
A = [1.6 -0.7;
1 0];
B = [0.5; 0];
C = [0.1 0.1];
D = 0;
sys = ss(A,B,C,D,0.2);
opt = RespConfig;
opt.Bias = 1;
opt.Amplitude = -2;
step(sys,opt)
Verwenden Sie lsim für Reaktionen auf beliebige Eingangssignale.
Vergleichen Sie die Sprungantwort eines parametrisch ermittelten Modells mit jener eines nicht-parametrischen (empirischen) Modells. Sehen Sie sich auch ihre 3 Konfidenzintervalle an.
Laden Sie die Daten.
load iddata1 z1
Schätzen Sie ein parametrisches Modell.
sys1 = ssest(z1,4);
Schätzen Sie ein nicht-parametrisches Modell.
sys2 = impulseest(z1);
Plotten Sie die Sprungantwort zum Vergleich.
t = (0:0.1:10)'; [y1, ~, ~, ysd1] = step(sys1,t); [y2, ~, ~, ysd2] = step(sys2,t); plot(t, y1, 'b', t, y1+3*ysd1, 'b:', t, y1-3*ysd1, 'b:') hold on plot(t, y2, 'g', t, y2+3*ysd2, 'g:', t, y2-3*ysd2, 'g:')
Berechnen Sie die Sprungantwort eines identifizierten Zeitreihenmodells.
Ein Zeitreihenmodell, auch Signalmodell genannt, ist ein Modell ohne gemessene Eingangssignale. Das Sprungdiagramm dieses Modells verwendet seinen (nicht gemessenen) Rauschkanal als Eingangskanal, an den das Sprungsignal angelegt wird.
Laden Sie die Daten.
load iddata9;Schätzen Sie ein Zeitreihenmodell.
sys = ar(z9, 4);
sys ist ein Modell der Form A y(t) = e(t), wobei e(t) den Rauschkanal darstellt. Zur Berechnung der Sprungantwort wird e(t) als ein Eingangskanal behandelt und e@y1 benannt.
Plotten Sie die Sprungantwort.
step(sys)
Validieren Sie die Linearisierung eines nichtlinearen ARX-Modells durch Vergleich der Sprungantworten mit kleiner Amplitude der linearen und nichtlinearen Modelle.
Laden Sie die Daten.
load iddata2 z2;
Schätzen Sie ein nichtlineares ARX-Modell.
nlsys = nlarx(z2,[4 3 10],idTreePartition,'custom',... {'sin(y1(t-2)*u1(t))+y1(t-2)*u1(t)+u1(t).*u1(t-13)',... 'y1(t-5)*y1(t-5)*y1(t-1)'},'nlr',[1:5, 7 9]);
Bestimmen Sie einen Gleichgewichtsbetriebspunkt für nlsys, der einem stationären Eingangswert von 1 entspricht.
u0 = 1;
[X,~,r] = findop(nlsys, 'steady', 1);
y0 = r.SignalLevels.Output;Ermitteln Sie eine lineare Näherung von nlsys an diesem Betriebspunkt.
sys = linearize(nlsys,u0,X);
Validieren Sie die Nützlichkeit von sys durch einen Vergleich seiner Sprungantwort bei kleinen Amplituden mit derjenigen von nlsys.
Das nichtlineare System nlsys arbeitet auf einem Gleichgewichtsniveau, das durch (u0,y0) vorgegeben wird. Führen Sie eine Sprungstörung der Größe 0,1 um diesen stationären Zustand ein und berechnen Sie die entsprechende Reaktion.
opt = RespConfig; opt.InputOffset = u0; opt.Amplitude = 0.1; t = (0:0.1:10)'; ynl = step(nlsys, t, opt);
Das lineare System sys drückt die Beziehung zwischen den Störungen am Eingang und der entsprechenden Störung am Ausgang aus. Sie kennt die Gleichgewichtswerte des nichtlinearen Systems nicht.
Plotten Sie die Sprungantwort des linearen Systems.
opt = RespConfig; opt.Amplitude = 0.1; yl = step(sys, t, opt);
Addieren Sie den Offset für den stationären Zustand, y0, zu der Antwort des linearen Systems und plotten Sie die Antworten.
plot(t, ynl, t, yl+y0) legend('Nonlinear', 'Linear with offset')
Berechnen und plotten Sie die Sprungantwort eines LPV-Modells (lpvss). Dieses Beispiel simuliert die in fcnMaglev.m definierte Sprungantwort im geschlossenen Regelkreis eines Modells einer schwebenden Kugel auf eine Störung .
Erstellen Sie das Modell und diskretisieren Sie es.
hmin = 0.05; hmax = 0.25; h0 = (hmin+hmax)/2; Ts = 0.01; Glpv = lpvss("h",@fcnMaglev,0,0,h0); Glpvd = c2d(Glpv,Ts,"tustin");
Probieren Sie das LPV-Modell mit drei Höhenwerten aus und stellen Sie einen PID-Regler ein.
hpid = linspace(hmin,hmax,3);
[Ga,Goffset] = sample(Glpvd,[],hpid);
wc = 50;
Ka = pidtune(Ga,"pidf",wc);
Ka.Tf = 0.01;Erstellen Sie den verstärkungsgesteuerten PID-Regler.
Ka.SamplingGrid = struct("h",hpid); Koffset = struct("y",{Goffset.u}); Clpv = ssInterpolant(ss(Ka),Koffset);
Erstellen Sie das Modell des geschlossenen Regelkreises.
CL = feedback(Glpvd*[1,Clpv],1,2,1);
CL.InputName = {'du';'href'};
CL.OutputName = "h";Ermitteln Sie den stationären Strom für = , um eine geeignete Größe für die Sprungstörung am Anlageneingang zu berechnen.
[~,~,~,~,~,~,~,u0] = Glpv.DataFunction(0,h0);
Berechnen und plotten Sie die Antwort auf die Eingangsstörung und die Sprungänderung des Sollwerts. Setzen Sie die Eingangssignal-Grundwerte = 0 und = , um den stationären Anfangszustand festzulegen.
t = 0:Ts:2; pFcn = @(k,x,u) x(1); Config = RespConfig( ... Bias=[0;h0], ... Amplitude=0.2*[u0;h0]*Ts, ... Delay=0.5, ... InitialParameter=h0); step(CL,t,pFcn,Config) title("Current Step Disturbance and Height Step Change")
Erstellen Sie ein Zustandsraummodell mit komplexen Koeffizienten.
A = [-2-2i -2;1 0]; B = [2;0]; C = [0 0.5+2.5i]; D = 0; sys = ss(A,B,C,D);
Berechnen Sie die Sprungantwort des Systems.
[y,t] = step(sys);
Die resultierenden Antwortdaten enthalten komplexe Ausgangswerte.
y
y = 369×1 complex
0.0000 + 0.0000i
0.0018 + 0.0075i
0.0079 + 0.0286i
0.0191 + 0.0612i
0.0360 + 0.1033i
0.0588 + 0.1531i
0.0874 + 0.2089i
0.1215 + 0.2690i
0.1609 + 0.3320i
0.2048 + 0.3969i
0.2528 + 0.4624i
0.3041 + 0.5279i
0.3580 + 0.5925i
0.4138 + 0.6558i
0.4708 + 0.7173i
⋮
Eingabeargumente
Ausgangsargumente
Tipps
Verwenden Sie
lsim, um die Reaktionen des Systems auf beliebige Eingangssignale zu simulieren.Verwenden Sie stattdessen die Funktion
stepplot, wenn Sie weitere Optionen zur Anpassung von Diagrammen benötigen.Diagramme, die mit
steperstellt werden, unterstützen keine mehrzeiligen Titel oder Beschriftungen, die als String-Arrays oder Zellenarrays von Zeichenvektoren angegeben sind. Verwenden Sie zur Angabe mehrzeilige Titel und Beschriftungen eine einzelne Zeichenkette mit einemnewline-Zeichen.step(sys,u,t) title("first line" + newline + "second line");
Algorithmen
Um Abtastungen von zeitkontinuierlichen Modellen ohne interne Verzögerungen zu erhalten, konvertiert step solche Modelle in Zustandsraummodelle und diskretisiert sie unter Verwendung einer Haltefunktion nullter Ordnung für die Eingänge. step wählt die Abtastzeit für diese Diskretisierung automatisch auf der Grundlage der Systemdynamik, es sei denn, Sie geben den Eingangszeitvektor t in der Form t = T0:dt:Tf an. In diesem Fall verwendet step als Abtastzeit dt. Die resultierenden Simulationszeitschritte tOut werden mit dem Abstand dt gleichmäßig abgetastet.
Bei Systemen mit internen Verzögerungen verwendet die Control System Toolbox™-Software Solver mit variablen Schritten. Infolgedessen werden die Zeitschritte tOut nicht gleichmäßig abgetastet.
Referenzen
[1] L.F. Shampine and P. Gahinet, "Delay-differential-algebraic equations in control theory," Applied Numerical Mathematics, Vol. 56, Issues 3–4, pp. 574–588.
