FEEDBACK zum Schließen von Rückkopplungsschleifen verwenden

Zwei Möglichkeiten zum Schließen von Rückkopplungsschleifen

Betrachten Sie die folgende Rückkopplungsschleife:

Dabei gilt:

K = 2;
G = tf([1 2],[1 .5 3])

G =
 
       s + 2
  ---------------
  s^2 + 0.5 s + 3
 
Continuous-time transfer function.

Sie können die Transferfunktion H des geschlossenen Regelkreises von r nach y auf mindestens zwei Arten berechnen:

Um H mit Hilfe von feedback zu berechnen, geben Sie ein:

H = feedback(G,K)

H =
 
       s + 2
  ---------------
  s^2 + 2.5 s + 7
 
Continuous-time transfer function.

Um H anhand der Formel zu berechnen, geben Sie ein:

H2 = G/(1+G*K)

H2 =
 
        s^3 + 2.5 s^2 + 4 s + 6
  -----------------------------------
  s^4 + 3 s^3 + 11.25 s^2 + 11 s + 21
 
Continuous-time transfer function.

Warum die Verwendung von FEEDBACK besser ist

Ein Hauptproblem bei der Berechnung von H aus der Formel ist, dass dadurch die Ordnung der Transferfunktionen des geschlossenen Regelkreises in die Höhe getrieben wird. Im Beispiel oben hat H2 die doppelte Ordnung von H. Das liegt daran, dass der Ausdruck G/(1+G*K) als Verhältnis der beiden Transferfunktionen G und 1+G*K bewertet wird. Falls

dann wird G/(1+G*K) ausgewertet als:

Infolgedessen werden die Polstellen von G sowohl zum Zähler als auch zum Nenner von H hinzugefügt. Sie können dies bestätigen, wenn Sie sich die ZPK-Darstellung ansehen:

zpk(H2)

ans =
 
       (s+2) (s^2 + 0.5s + 3)
  ---------------------------------
  (s^2 + 0.5s + 3) (s^2 + 2.5s + 7)
 
Continuous-time zero/pole/gain model.

Dieser Überschuss an Pol- und Nullstellen kann sich negativ auf die Genauigkeit der Ergebnisse auswirken, wenn es sich um Transferfunktionen hoher Ordnung handelt, wie das nächste Beispiel zeigt. In diesem Beispiel geht es um eine Transferfunktion 17. Ordnung, der Übertragungsfunktion G. Wie zuvor verwenden Sie beide Ansätze, um die Transferfunktion des geschlossenen Regelkreises zu berechnen für K=1 zu berechnen.

load numdemo G
H1 = feedback(G,1);          % good
H2 = G/(1+G);                % bad

Um einen Anhaltspunkt zu haben, berechnen Sie auch ein FRD-Modell, das den Frequenzgang von G enthält und wenden Sie feedback direkt auf die Frequenzgangdaten an:

w = logspace(2,5.1,100);
H0 = feedback(frd(G,w),1);

Vergleichen Sie dann die Größenordnungen der Rückkopplungen:

h = sigmaplot(H0,'b',H1,'g--',H2,'r');
legend('Reference H0','H1=feedback(G,1)','H2=G/(1+G)','location','southwest')
setoptions(h,'YlimMode','manual','Ylim',{[-60 0]})

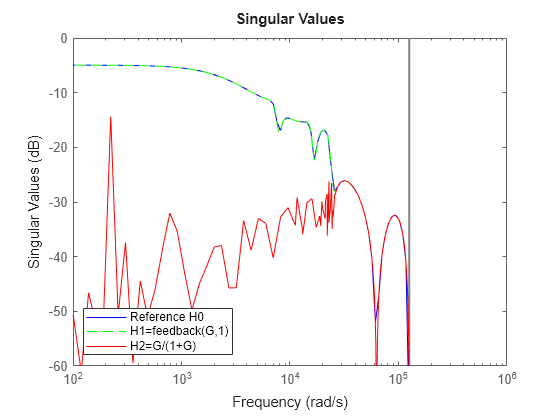
Der Frequenzgang von H2 ist für Frequenzen unter 2e4 rad/s ungenau. Diese Ungenauigkeit lässt sich auf die zusätzliche (auslöschende) Dynamik in der Nähe von z=1 zurückführen. Genauer gesagt hat H2 etwa doppelt so viele Pol- und Nullstellen nahe z=1 wie H1. Infolgedessen hat H2(z) in der Nähe von z=1 eine viel schlechtere Genauigkeit, was die Antwort bei niedrigen Frequenzen verzerrt. Siehe das Beispiel Using the Right Model Representation für weitere Einzelheiten.