Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

c2d

Konvertieren eines Modells von kontinuierlicher zu diskreter Zeit

Syntax

sysd = c2d(sysc,Ts)

sysd = c2d(sysc,Ts,method)

sysd = c2d(sysc,Ts,opts)

[sysd,G] = c2d(___)

Beschreibung

sysd = c2d(sysc,Ts) diskretisiert das zeitkontinuierliche dynamische Systemmodell sysc mithilfe einer Haltefunktion nullter Ordnung für die Eingänge und einer Abtastzeit von Ts.

sysd = c2d(sysc,Ts,method) legt die Diskretisierungsmethode fest.

sysd = c2d(sysc,Ts,opts) legt weitere Optionen für die Diskretisierung fest.

[sysd,G] = c2d(___), wobei sysc ein Zustandsraummodell ist, gibt eine Matrix G aus, die die kontinuierlichen Ausgangsbedingungen x₀ und u₀ des Zustandsraummodells auf dem zeitdiskreten anfänglichen Zustandsvektor x[0]. abbildet.

Beispiele

Diskretisieren einer Transferfunktion

Diskretisieren Sie die folgende zeitkontinuierliche Transferfunktion:

$$H\left(s\right)=e^{-0.3s}\frac{s-1}{s^2+4s+5}.$$

Das System weist eine Eingangsverzögerung von 0,3 s auf. Diskretisieren Sie das System mithilfe der Dreiecksnäherung (Haltefunktion erster Ordnung) mit einer Abtastzeit Ts = 0,1 s.

H = tf([1 -1],[1 4 5],'InputDelay', 0.3); 
Hd = c2d(H,0.1,'foh');

Vergleichen Sie die Schrittantworten der zeitkontinuierlichen und diskretisierten Systeme.

step(H,'-',Hd,'--')

Diskretisieren eines Modells mit in Koeffizienten absorbierter fraktionaler Verzögerung

Diskretisieren Sie die folgende verzögerte Transferfunktion mit einer Haltefunktion nullter Ordnung für den Eingang und einer Abtastrate von 10 Hz.

$$H\left(s\right)=e^{-0.25s}\frac{10}{s^2+3s+10}.$$

h = tf(10,[1 3 10],'IODelay',0.25); 
hd = c2d(h,0.1)

hd =
 
           0.01187 z^2 + 0.06408 z + 0.009721
  z^(-3) * ----------------------------------
                 z^2 - 1.655 z + 0.7408
 
Sample time: 0.1 seconds
Discrete-time transfer function.

In diesem Beispiel weist das diskretisierte Modell hd eine Verzögerung von drei Abtastzeitperioden auf. Der Diskretisierungsalgorithmus absorbiert die verbleibende Verzögerung einer halben Periode in die Koeffizienten von hd.

Vergleichen Sie die Schrittantworten der zeitkontinuierlichen und diskretisierten Modelle.

step(h,'--',hd,'-')

Diskretisieren eines Modells mit angenäherter fraktionaler Verzögerung

Seit R2024a

Erstellen Sie ein zeitkontinuierliches Zustandsraummodell mit zwei Zuständen und einer Eingangsverzögerung.

sys = ss(tf([1,2],[1,4,2]));
sys.InputDelay = 2.7

sys =
 
  A = 
       x1  x2
   x1  -4  -2
   x2   1   0
 
  B = 
       u1
   x1   2
   x2   0
 
  C = 
        x1   x2
   y1  0.5    1
 
  D = 
       u1
   y1   0
 
  Input delays (seconds): 2.7 
 
Continuous-time state-space model.

Diskretisieren Sie das Modell mithilfe der Tustin-Diskretisierungsmethode und einem Thiran-Filter, um fraktionale Verzögerungen zu modellieren. Die Abtastzeit Ts = 1 Sekunde.

opt = c2dOptions('Method','tustin','ThiranOrder',3);
sysd1 = c2d(sys,1,opt)

sysd1 =
 
  A = 
            x1       x2
   x1  -0.4286  -0.5714
   x2   0.2857   0.7143
 
  B = 
           u1
   x1  0.5714
   x2  0.2857
 
  C = 
           x1      x2
   y1  0.2857  0.7143
 
  D = 
           u1
   y1  0.2857
 
  (values computed with all internal delays set to zero)

  Internal delays (sampling periods): 1  1  1 
 
Sample time: 1 seconds
Discrete-time state-space model.

Standardmäßig modelliert die Funktion weitere Verzögerungen als interne Verzögerungen im diskretisierten Modell. Um weitere Verzögerungen als Zustände im diskretisierten Modell zu modellieren, setzen Sie die Option DelayModeling von c2dOptions auf 'state'.

opt2 = c2dOptions('Method','tustin','ThiranOrder',3,'DelayModeling','state');
sysd2 = c2d(sys,1,opt2)

sysd2 =
 
  A = 
              x1         x2         x3         x4         x5
   x1    -0.4286    -0.5714   -0.00265    0.06954      2.286
   x2     0.2857     0.7143  -0.001325    0.03477      1.143
   x3          0          0    -0.2432     0.1449    -0.1153
   x4          0          0       0.25          0          0
   x5          0          0          0      0.125          0
 
  B = 
             u1
   x1  0.002058
   x2  0.001029
   x3         8
   x4         0
   x5         0
 
  C = 
              x1         x2         x3         x4         x5
   y1     0.2857     0.7143  -0.001325    0.03477      1.143
 
  D = 
             u1
   y1  0.001029
 
Sample time: 1 seconds
Discrete-time state-space model.

Das diskretisierte Modell enthält nun drei weitere Zustände x3, x4 und x5, was einem Thiran-Filter dritter Ordnung entspricht. Da die durch die Abtastzeit geteilte Zeitverzögerung 2,7 ist, kann der Thiran-Filter dritter Ordnung ('ThiranOrder' = 3) die gesamte Zeitverzögerung annähern.

Diskretisieren eines identifizierten Modells

Schätzen Sie eine zeitkontinuierliche Transferfunktion und diskretisieren Sie diese.

load iddata1
sys1c = tfest(z1,2);
sys1d = c2d(sys1c,0.1,'zoh');

Schätzen Sie eine zeitdiskrete Transferfunktion zweiter Ordnung.

sys2d = tfest(z1,2,'Ts',0.1);

Vergleichen Sie die Antwort des diskretisierten zeitkontinuierlichen Transferfunktionsmodells sys1d mit der Antwort des direkt geschätzten zeitdiskreten Modells sys2d.

compare(z1,sys1d,sys2d)

Die zwei Systeme sind nahezu identisch.

Erstellen eines Prädiktormodells

Diskretisieren Sie ein identifiziertes Zustandsraummodell, um einen Prädiktor, der die Antwort einen Schritt in der Zukunft vorausberechnet, zu erstellen.

Erstellen Sie ein zeitkontinuierliches, identifiziertes Zustandsraummodell mithilfe von Schätzdaten.

load iddata2
sysc = ssest(z2,4);

Prognostizieren Sie die prognostizierte Antwort sysc einen Schritt in der Zukunft.

predict(sysc,z2)

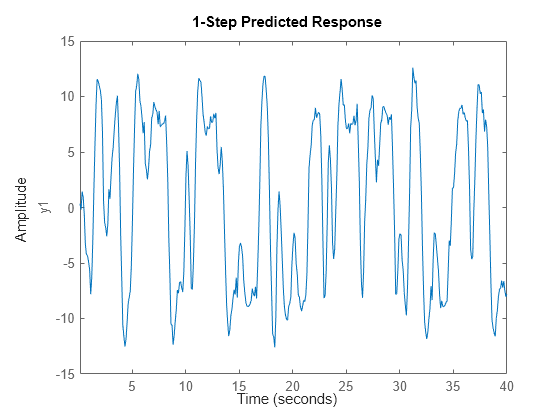
Diskretisieren Sie das Modell.

sysd = c2d(sysc,0.1,'zoh');

Erstellen Sie ein Prädiktormodell aus dem diskretisierten Modell sysd.

[A,B,C,D,K] = idssdata(sysd);
Predictor = ss(A-K*C,[K B-K*D],C,[0 D],0.1);

Predictor ist ein Modell mit zwei Eingängen, das die gemessenen Ausgangs- und Eingangssignale ([z1.y z1.u]) verwendet, um die prognostizierte Antwort von sysc einen Schritt in der Zukunft zu berechnen.

Simulieren Sie das Prädiktormodell, um dieselbe Antwort wie der Befehl predict zu erhalten.

lsim(Predictor,[z2.y,z2.u])

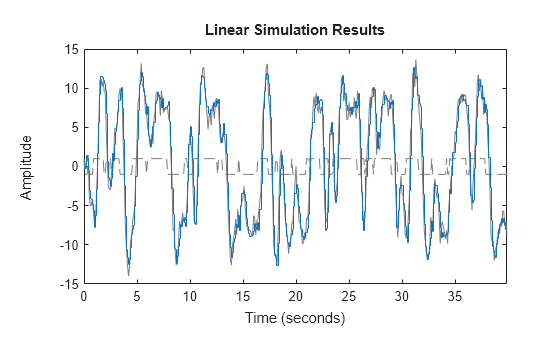
Die Simulation des Prädiktormodells gibt dieselbe Antwort wie predict(sysc,z2) aus.

Eingabeargumente

sysc — Zeitkontinuierliches dynamisches System

Dynamisches Systemmodell

Zeitkontinuierliche Modelle, festgelegt als dynamisches Systemmodell wie tf, ss oder zpk. sysc kann keine Frequenzantwort-Datenmodell sein. sysc kann ein SISO- oder MIMO-System sein, mit der Ausnahme, dass die Diskretisierungsmethode 'matched' nur SISO-Systeme unterstützt.

sysc kann Eingangs-/Ausgangs- oder interne Zeitverzögerungen aufweisen; die Methoden 'matched', 'impulse' und 'least-squares' unterstützen jedoch keine Zustandsraummodelle mit internen Zeitverzögerungen.

Die folgenden identifizierten linearen Systeme können nicht direkt diskretisiert werden.

• idgrey-Modelle, deren FunctionType 'c' ist. Konvertieren Sie diese zunächst zu einem idss-Modell.

• idproc-Modelle. Konvertieren Sie diese zunächst zu einem idtf- oder idpoly-Modell.

Ts — Abtastzeit

Positiver Skalar

Abtastzeit, angegeben als positiver Skalar, der die Abtastperiode des resultierenden zeitdiskreten Systems darstellt. Ts ist in TimeUnit, der Eigenschaft sysc.TimeUnit.

method — Diskretisierungsmethode

'zoh' (Standardeinstellung) | 'foh' | 'impulse' | 'tustin' | 'matched' | 'least-squares' | 'damped'

Diskretisierungsmethode, angegeben als einer der folgenden Werte:

• 'zoh' – Haltefunktion nullter Ordnung (Standardwert). Geht davon aus, dass die Regeleingänge über die Abtastzeit Ts hinweg konstant sind.

• 'foh' – Dreiecks-Annäherung (abgeänderte Haltefunktion nullter Ordnung). Geht davon aus, dass die Regeleingänge über die Abtastzeit Ts hinweg linear sind.

• 'impulse' – Impuls-invariante Diskretisierung

• 'tustin' – Bilineare (Tustin-) Methode. Um diese Methode mit Frequenz-Vorverzerrung (früher als 'prewarp'-Methode bekannt) festzulegen, verwenden Sie die Option PrewarpFrequency von c2dOptions.

• 'matched' – Null-Polstellen-Abgleichmethode

• 'least-squares' – Least-Squares-Methode

• 'damped' – Gedämpfte Tustin-Annäherung auf Grundlage der TRBDF2-Formel, nur für sparss-Modelle.

Weitere Informationen zu den Algorithmen für jede Konvertierungsmethode finden Sie unter Continuous-Discrete Conversion Methods.

opts — Diskretisierungsoptionen

c2dOptions-Objekt

Diskretisierungsoptionen, angegeben als c2dOptions-Objekt. Sie können beispielsweise die Vorverzerrungs-Frequenz, die Ordnung des Thiran-Filters oder die Diskretisierungsmethode als Option festlegen.

Ausgangsargumente

sysd — Zeitdiskretes Modell

Dynamisches Systemmodell

Zeitdiskretes Modell, ausgegeben als dynamisches Systemmodell mit demselben Typ wie das Eingangssystem sysc.

Ist sysc ein identifiziertes Modell (IDLTI), gilt für sysd:

• Es umfasst sowohl die gemessene Komponente als auch die Rauschkomponente von sysc. Die Innovations-Varianz λ des zeitkontinuierlichen identifizierten Modells sysc, gespeichert in der Eigenschaft NoiseVariance, wird als Intensität der spektralen Dichte des Rauschspektrums interpretiert. Die Rauschvarianz in sysd entspricht daher λ/Ts.

• Es umfasst nicht die geschätzte Parameter-Kovarianz von sysc. Wenn Sie die Kovarianz bei der Diskretisierung des Modells übernehmen möchten, verwenden Sie translatecov.

G — Abbilden der kontinuierlichen Ausgangsbedingungen von Zustandsraummodellen auf zeitdiskreten Anfangszustandvektor

Matrix

Abbilden der zeitkontinuierlichen Ausgangsbedingungen x₀ und u₀ des Zustandsraum-Modells sysc auf den zeitdiskreten Anfangszustand-Vektor x[0], ausgegeben als Matrix. Die Abbildung der Ausgangsbedingungen auf den Anfangszustand-Vektor erfolgt folgendermaßen:

$$x\left[0\right]=G\cdot \left[\begin{array}{c}{x}_0\\ u_0\end{array}\right]$$

Bei Zustandsraummodellen mit Zeitverzögerungen fügt c2d der Matrix G Nullen hinzu, um durch die Diskretisierung der Verzögerungen entstehende weitere Zustände aufnehmen zu können. Weitere Informationen zur Modellierung von Zeitverzögerungen in diskretisierten Systemen finden Sie unter Continuous-Discrete Conversion Methods.

Versionsverlauf

Eingeführt vor R2006a

R2024a: Fügt während der Konvertierung keine weiteren Zustände hinzu

Der Befehl c2d fügt bei der Modellierung zusätzlicher Verzögerungen keine weiteren Zustände mehr hinzu. Standardmäßig verwendet c2d nun interne Verzögerungen und gibt das diskretisierte Modell mit derselben Anzahl Zustände aus. Dies führt zu einem besser prognostizierbaren Verhalten und vereinfacht die Abbildung des Anfangszustand von kontinuierlicher zu diskreter Zeit.

Um zum alten Verhalten vor Version R2024a zurückzukehren, erstellen Sie einen Satz Optionen mithilfe von c2dOptions und setzen Sie DelayModeling auf "state".

R2024a: Unterstützung für mechss-Modelle

Sie können mechss-Modelle nun mithilfe der bilinearen Tustin-Annäherungsmethode diskretisieren. Bei mechss-Modellen berechnet die 'tustin'-Methode eine Tustin-Diskretisierung der zweiten Ordnung. Dies entspricht der Anwendung von Tustin auf ein sparss erster Ordnung, äquivalent zum mechss-Modell.

R2024a: Unterstützung für Modelle mit Versätzen und weiteren Verbesserungen

Sie können nun mithilfe von c2d Modelle mit Versätzen diskretisieren, wie beispielsweise Rastermodelle mit variablen linearen Parametern.

Zudem bietet c2dOptions zwei neue Optionen

• DelayModeling – Legt fest, ob zusätzliche Verzögerungen als interne Verzögerungen (Standardwert) oder zusätzliche Zustände modelliert werden sollen.

• Consistency – Erzwingt Zustands- und Verzögerungskonsistenz in Zustandsraum-Arrays. Diese Option ist bei der Diskretisierung von Raster-LPV- oder LTV-Modellen nützlich.

Siehe auch

c2dOptions | d2c | d2d | thiran | translatecov (System Identification Toolbox) | Konvertierung der Modellrate

Themen

• Dynamische Systemmodelle
• Discretize a Compensator
• Continuous-Discrete Conversion Methods