Trigonometric Function

Specified trigonometric function on input

• 

Libraries:
Simulink / Math Operations
HDL Coder / Math Operations
HDL Coder / HDL Floating Point Operations

Description

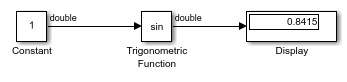
The Trigonometric Function block performs common trigonometric functions and outputs the result in rad or rev.

Supported Functions

You can select one of these functions from the Function parameter list.

Function	Description	Mathematical Expression	MATLAB® Equivalent
sin	Sine of the input	sin(u)	sin
cos	Cosine of the input	cos(u)	cos
tan	Tangent of the input	tan(u)	tan
asin	Inverse sine of the input	asin(u)	asin
acos	Inverse cosine of the input	acos(u)	acos
atan	Inverse tangent of the input	atan(u)	atan
atan2	Four-quadrant inverse tangent of the input	atan2(u)	atan2
sinh	Hyperbolic sine of the input	sinh(u)	sinh
cosh	Hyperbolic cosine of the input	cosh(u)	cosh
tanh	Hyperbolic tangent of the input	tanh(u)	tanh
asinh	Inverse hyperbolic sine of the input	asinh(u)	asinh
acosh	Inverse hyperbolic cosine of the input	acosh(u)	acosh
atanh	Inverse hyperbolic tangent of the input	atanh(u)	atanh
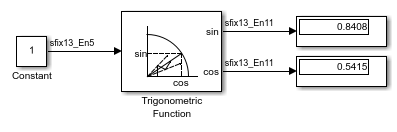
sincos	Sine of the input; cosine of the input	—	—
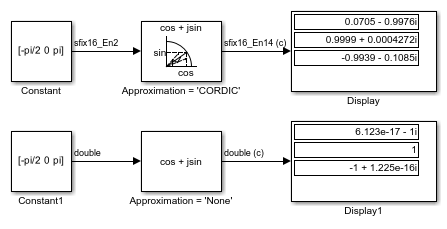
cos + jsin	Complex exponential of the input	—	—

CORDIC Approximation Method

CORDIC is an acronym for COordinate Rotation DIgital Computer. The Givens rotation-based CORDIC algorithm is one of the most hardware-efficient algorithms available because it requires only iterative shift-add operations. For more information, see More About. The block input has further requirements.

For more information on when you set Function to sin, cos, sincos, or cos + jsin and set the Approximation method to CORDIC, see Port_1.

This table summarizes what happens for an invalid input.

Block Usage	Effect of Invalid Input
Simulation modes	An error appears.
Generated code	Undefined behavior occurs. Avoid relying on undefined behavior for generated code.

Lookup Approximation Method

For more information on when you set Function to sin, cos, sincos, or cos + jsin and set the Approximation method to Lookup, see Port_1.

Examples

sin Function with Floating-Point Input

This example shows how to use the Trigonometric Function block to compute the sine of a floating-point input. The output of the Trigonometric Function block has the same data type as the input because the input data type is floating-point and the Approximation method is none.

sincos Function with Fixed-Point Input

This example shows how to use the Trigonometric Function block to compute the CORDIC approximation of sincos for a fixed-point input signal.

The Trigonometric Function block parameters are:

• Function: sincos

• Approximation method: CORDIC

• Number of iterations: 11

When using the CORDIC approximation method, the input to the Trigonometric Function block must be in the range [-2pi,2pi). The output type of the Trigonometric Function block is fixdt(1,13,11) because the input is a fixed-point signal and the Approximation method is set to CORDIC. The output fraction length equals the input word length minus two.

Trigonometric Function Block Behavior for Complex Exponential Output

This example compares the complex exponential output for two different configurations of the Trigonometric Function block.

When the Approximation method is CORDIC, the input data type can be fixed point, in this case: fixdt(1,16,2). The output data type is fixdt(1,16,14) because the output fraction length equals the input word length minus two.

When the Approximation method is None, the input data type must be floating point. The output data type is the same as the input data type.

Ports

Input

Port_1 — Input signal

scalar | vector | matrix

Input specified as a scalar, vector, or matrix. The block accepts input signals of the following data types:

Functions	Input Data Types
sin cos sincos cos + jsin atan2	Floating point Fixed point (only when Approximation method is CORDIC)
tan asin acos atan sinh cosh tanh asinh acosh atanh	Floating point

CORDIC approximation fixed-point type propagations:

Input Data Type	Function	Output Data Type
Fixed point, signed or unsigned	sin, cos, sincos, and cos + jsin	fixdt(1, WL, WL - 2) where WL is the input word length This fixed-point type provides the best precision for the CORDIC algorithm.
Fixed point, signed	atan2	fixdt(1, WL, WL – 3)
Fixed point, unsigned	atan2	fixdt(1, WL, WL – 2)

Lookup approximation fixed-point type propagations:

Input Data Type	Function	Output Data Type
Fixed point, signed	sin, cos, sincos, cos + jsin, atan2	fixdt(1, WL, FL)
Fixed point, unsigned	sin, cos, sincos, cos + jsin, atan2	fixdt(1, WL - 1, FL)

Dependencies

• When you set Function to atan2, the block shows two input ports. The first input (Port_1) is the y-axis or imaginary part of the function argument. The second input (Port_2) is the x-axis or real part of the function argument.

• You can use floating-point input signals when you set Approximation method to None, CORDIC, or Lookup. However, the block output data type depends on which of these approximation method options you choose.

  Input Data Type	Approximation Method	Output Data Type
  Floating point	None	Depends on your selection for Output signal type. Options are auto (same data type as input), real, or complex.
  Floating point	CORDIC	Same as input. Output signal type is not available when you use the CORDIC approximation method to compute the block output.
  Floating point	Lookup	Same as input. Output signal type is not available when you use the Lookup approximation method to compute the block output.

For CORDIC and Lookup approximations:

• Input must be real for the sin, cos, sincos, cos + jsin, and atan2 functions.

• Output is real for the sin, cos, sincos, and atan2 functions.

• Output is complex for the cos + jsin function.

Limitations

• You can use fixed-point input signals only when Approximation method is set to CORDIC or Lookup. The CORDIC and Lookup approximations are available for the sin, cos, sincos, cos + jsin, and atan2 functions.

• Complex input signals are supported for all functions in this block except atan2.

• When you set Approximation method to Lookup, the number of data points are limited by:

  • smallEnoughNumDataPoints = 2(inputFractionLen-2)+1

  • bigEnoughFractionLen = log2(numberOfDataPoints - 1)+2

  where:

  • smallEnoughNumDataPoints is the maximum number of data points represented by specified input fraction length, inputFractionLen.

  • bigEnoughFractionLen is the minimum fraction length needed to represent specified number of data points, numberOfDataPoints.

• When you set Function to sin, cos, sincos, or cos + jsin and set the Approximation method to CORDIC, the block has these limitations:

  • When you use signed fixed-point types, the input angle must fall within the range [–2π, 2π) rad.

  • When you use unsigned fixed-point types, the input angle must fall within the range [0, 2π) rad.

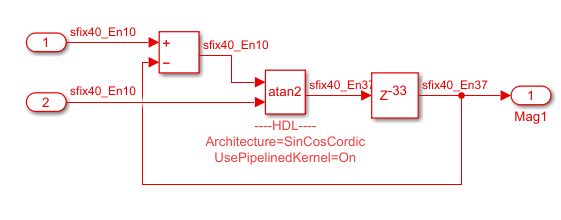
  When you set Function to atan2 and the Approximation method to CORDIC, the block has these limitations:

  • Inputs must be the same size, or at least one value must be a scalar value.

  • Both inputs must have the same data type.

  • When you use signed fixed-point types, the word length must be 126 or less.

  • When you use unsigned fixed-point types, the word length must be 125 or less.

• When you set Function to sin, cos, sincos, or cos + jsin and set the Approximation method to Lookup, the block has these limitations.

  • When you use signed fixed-point types, the input angle must fall within the range [-2π,2π] rad.

  • When you use unsigned fixed-point types, the input angle must fall within the range [0,2π) rad.

  • When you set Function to atan2 and the Approximation method to Lookup, the block has these limitations:

    • Inputs must be the same size, or at least one value must be a scalar value.

    • Both inputs must have the same data type.

Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point

Port_2 — x-axis or real part of the function argument for atan2

scalar | vector | matrix

Input the x-axis or real part of the function argument for atan2. When you set Function to atan2, the block shows two input ports. The first input (Port_1) is the y-axis or imaginary part of the function argument. The second input (Port_2) is the x-axis or real part of the function argument. (See Identify Port Location on Rotated or Flipped Block for a description of the port order for various block orientations.)

Dependencies

To enable this port, set Function to atan2.

Limitations

• Fixed-point input signals are supported only when you set Approximation method to CORDIC or Lookup.

Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point

Output

Port_1 — Specified trigonometric function of input

scalar | vector | matrix

Result of applying the specified trigonometric function to one or more inputs in rad. Each function supports:

• Scalar operations

• Element-wise vector and matrix operations

Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point

sin — Sine of input signal

scalar | vector | matrix

Sine of the input signal, in rad and rev.

Dependencies

To enable this port, set Function to sincos.

Limitations

Fixed-point input signals are supported only when you set Approximation method to CORDIC or Lookup.

Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point

cos — Cosine of input signal

scalar | vector | matrix

Cosine of the input signal, in rad and rev.

Dependencies

To enable this port, set Function to sincos.

Limitations

Fixed-point input signals are supported only when you set Approximation method to CORDIC or Lookup.

Data Types: half | single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point

Parameters

Algorithm

Function — Trigonometric function

sin (default) | cos | tan | asin | acos | atan | atan2 | sinh | cosh | tanh | asinh | acosh | atanh | sincos | cos + jsin

Specify the trigonometric function. The name of the function on the block icon changes to match your selection.

For more information on when you set Function to sin, cos, sincos, or cos + jsin and set the Approximation method to CORDIC, see Limitations.

Programmatic Use

Block Parameter: Operator

Type: character vector

Values: 'sin' | 'cos' | 'tan' | 'asin' | 'acos' | 'atan' | 'atan2' | 'sinh' | 'cosh' | 'tanh' | 'asinh' | 'acosh' | 'atanh' | 'sincos' | 'cos + jsin'

Default: 'sin'

Approximation method — CORDIC, Lookup, or none

None (default) | CORDIC | Lookup

Specify the type of approximation for computing output.

Approximation Method	Data Types Supported	When to Use This Method
None (default)	Floating point	You want to use the default Taylor series algorithm.
CORDIC	Floating point and fixed point	You want a fast, approximate iterative calculation.
Lookup	Floating point and fixed point (double and single) with a Bias value of 0 and a Slope value of the power of 2	You want a fast, approximate lookup table implementation.

For more information on when you set Function to sin, cos, sincos, or cos + jsin and set the Approximation method to CORDIC, see Limitations.

Dependencies

• To enable this parameter, set Function to sin, cos, sincos, cos + jsin, or atan2.

• To use fixed-point input signals, you must set Approximation method to CORDIC or Lookup.

• To enable the Table data type parameter, set this method to Lookup.

Programmatic Use

Block Parameter: ApproximationMethod

Type: character vector

Values: 'None' | 'CORDIC' | 'Lookup'

Default: 'None'

Interpolation method — Method of interpolation between breakpoint values

Linear point-slope (default) | Flat

When an input falls between breakpoint values, the block interpolates the output value using neighboring breakpoints. For more information on interpolation methods, see Interpolation Methods.

Programmatic Use

Block Parameter: InterpMethod

Type: character vector

Values: 'Linear point-slope' | 'Flat'

Default: 'Linear point-slope'

Number of iterations — Number of iterations for CORDIC algorithm

11 (default) | positive integer, less than or equal to word length of fixed-point input

Specify the number of iterations to perform the CORDIC algorithm. The default value is 11.

• When the block input uses a floating-point data type, the number of iterations can be a positive integer.

• When the block input is a fixed-point data type, the number of iterations cannot exceed the word length.

  For example, if the block input is fixdt(1,16,15), the word length is 16. In this case, the number of iterations cannot exceed 16.

Dependencies

To enable this parameter, you must set the Function and Approximation method parameters as follows:

• Set Function to sin, cos, sincos, cos + jsin, or atan2.

• Set Approximation method to CORDIC.

Programmatic Use

Block Parameter: NumberOfIterations

Type: character vector

Values: positive integer, less than or equal to word length of fixed-point input

Default: '11'

Angle unit — Angle unit

radian (default) | revolution

Specify the angle unit for lookup method as radian or revolution.

Dependencies

To enable this parameter:

• Set Function to sin, cos, sincos, cos + jsin, or atan2.

• Set Approximation method to Lookup.

Programmatic Use

Block Parameter: AngleUnit

Type: character vector

Values: 'radian' | 'revolution'

Default: 'radian'

Number of data points — Number of data points for lookup table

16 (default) | scalar

Specify the number of data points for lookup table as a scalar real number.

Dependencies

To enable this parameter:

• Set Function to sin, cos, sincos, cos + jsin, or atan2.

• Set Approximation method to Lookup.

Programmatic Use

Block Parameter: NumberOfDataPoints

Type: character vector

Values: scalar

Default: '16'

Output signal type — Complexity of output signal

auto (default) | real | complex

Specify the output signal type of the Trigonometric Function block as auto, real, or complex.

Function	Input Signal Type	Output Signal Type
		Auto	Real	Complex
Any selection for the Function parameter	real	real	real	complex
	complex	complex	error	complex

Dependencies

Setting Approximation method to CORDIC disables this parameter.

Note

When Function is atan2, complex input signals are not supported for simulation or code generation.

Programmatic Use

Block Parameter: OutputSignalType

Type: character vector

Values: 'auto' | 'real' | 'complex'

Default: 'auto'

Remove protection against out-of-range input — Remove protection against out-of-range input

off (default) | on

For acos and asin, select this check box to remove the protection against out-of-range inputs, which reduces redundancy.

• When you clear this check box, the protection is enabled. The block saturates out-of-range inputs to 1 or -1 before any operation is performed. Generated code contains code to check for out-of-range input.

• When you select this check box, the protection is removed. The block performs all operations on the input value without any changes. Generated code does not contain code to check for the out-of-range input.

Enabling this check box can eliminate redundancy if the input is already in range.

Dependencies

Setting Function to acos and asin enables this parameter.

Programmatic Use

Block Parameter: RemoveProtectionAgainstOutOfRangeInput

Type: character vector

Values: 'off' | 'on'

Default: 'off'

Sample time (-1 for inherited) — Interval between samples

-1 (default) | scalar | vector

Specify the time interval between samples. To inherit the sample time, set this parameter to -1. For more information, see Specify Sample Time.

Dependencies

This parameter is visible only if you set it to a value other than -1. To learn more, see Blocks for Which Sample Time Is Not Recommended.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	SampleTime
Values:	"-1" (default) | scalar or vector in quotes

Data Types

Table data type — Data type of table

Inherit: Inherit via input (default) | double | single | fixdt(1,16,0) | <data type expression>

Data type for the lookup table, specified as:

• Inherit: Inherit via input

• double

• single

• fixdt(1,16,0)

• <data type expression>

For more information on setting data types, see Control Data Types of Signals.

Programmatic Use

Block Parameter: TableDataTypeStr

Type: string scalar or character vector

Values: Inherit: Inherit via input | single | double | fixdt(1,16,0) | data type expression

Default: Inherit: Inherit via input

Mode — Category of data to specify

Inherit (default) | Built in | Fixed point | Expression

Select how you would like to specify the data type properties of the Output data type. You can choose:

• Inherit — Lets you specify a rule for inheriting a data type, for example, Inherit: Inherit via internal rule

• Built in— Lets you specify a built-in data type.

• Fixed point — Lets you specify the fixed-point attributes of the data type.

• Expression — Lets you specify an expression that evaluates to a valid data type, for example, fixdt([],16,0)

Dependencies

To enable this parameter, click >> at the Output data type parameter.

Signedness — Specify signed or unsigned

Signed (default) | Unsigned

Specify the Signedness for the Output data type.

Dependencies

To enable this parameter, set Mode to Fixed point.

Scaling — Method for scaling fixed-point data

Binary point (default)

Specify the Scaling for the Output data type.

Dependencies

To enable this parameter, set Mode to Fixed point.

Data type override — Specify data type override mode for this signal

Inherit | Off

Select the data type override mode for this signal.

• Inherit — Inherits the data type override setting specified for the model.

• Off — Ignores the data type override setting specified for the model and uses the fixed-point data type you specify

For more information, see Specify Data Types Using Data Type Assistant in the Simulink^® documentation.

Tips

The ability to turn off data type override for an individual data type provides greater control over the data types in your model when you apply data type override. For example, you can use this option to ensure that data types meet the requirements of downstream blocks regardless of the data type override setting.

Dependencies

To enable this parameter, click the Show data type assistant button, and set Mode to Built in or Fixed point.

Word length — Bit size of the word that holds the quantized integer

16 (default) | integer from 0 to 32

Specify the bit size of the word that holds the quantized integer. For more information, see Specifying a Fixed-Point Data Type.

Dependencies

To enable this parameter, set Mode to Fixed point.

Fraction length — Specify fraction length for fixed-point data type

0 (default) | scalar integer

Specify fraction length for fixed-point data type as a positive or negative integer. For more information, see Specifying a Fixed-Point Data Type.

Dependencies

To enable this parameter, set:

• Mode to Fixed point

• Scaling to Binary point

Block Characteristics

Data Types	double | fixed pointa | half | integera | single
Direct Feedthrough	yes
Multidimensional Signals	yes
Variable-Size Signals	yes
Zero-Crossing Detection	no
a This block supports fixed-point and base integer data types for 'Approximation method' CORDIC.

More About

CORDIC

CORDIC is an acronym for COordinate Rotation DIgital Computer. The Givens rotation-based CORDIC algorithm is one of the most hardware-efficient algorithms available because it requires only iterative shift-add operations (see References). The CORDIC algorithm eliminates the need for explicit multipliers. Using CORDIC, you can calculate various functions such as sine, cosine, arc sine, arc cosine, arc tangent, and vector magnitude. You can also use this algorithm for divide, square root, hyperbolic, and logarithmic functions.

Increasing the number of CORDIC iterations can produce more accurate results, but doing so increases the expense of the computation and adds latency.

References

[1] Volder, Jack E., “The CORDIC Trigonometric Computing Technique.” IRE Transactions on Electronic Computers EC-8 (1959); 330–334.

[2] Andraka, Ray “A Survey of CORDIC Algorithm for FPGA Based Computers.” Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays. Feb. 22–24 (1998): 191–200.

[3] Walther, J.S., “A Unified Algorithm for Elementary Functions,” Proceedings of the Spring Joint Computer Conference, May 18-20, 1971: 379–386.

[4] Schelin, Charles W., “Calculator Function Approximation,” The American Mathematical Monthly 90, no. 5 (1983): 317–325.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

Not all compilers support the asinh, acosh, and atanh functions. If you use a compiler that does not support those functions, a warning appears and the generated code fails to link.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

To generate HDL code from the blocks that use fixed-point data, set Architecture to Cordic or LUT. This table shows the functions the block supports for these setting:

Block Parameters	HDL Block Properties	Supported Functions
Set Approximation method to CORDIC, Number of data Points to any scalar real number.	Set Architecture to Cordic.	sin cos sincos cos+jsin atan2
Set Approximation method to Lookup, Interpolation method to Flat, Angle Unit to revolution, and Number of data Points to any scalar real number.	Set Architecture to LUT.	sin cos sincos cos+jsin

To generate HDL code for all functions of the blocks that use floating-point data, set the Approximation method block parameter to none, and the Output signal type parameter to auto or real or complex. Additionally, set the Architecture parameter in the HDL block properties to Trigonometric.

This block has multi-cycle implementations that introduce additional latency in the generated code. To see the added latency, view the generated model or validation model. See Generated Model and Validation Model (HDL Coder).

The latency calculation depends on the word length and LatencyStrategy settings. To view the latency calculation for fixed-point data types, see:

• Sin (HDL Coder)

• Cos (HDL Coder)

• Cos+jSin (HDL Coder)

• SinCos (HDL Coder)

• Atan2 (HDL Coder)

HDL Block Properties

General
ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).
LatencyStrategy	To enable this property for fixed-point types, set Function as sin, cos, sincos, cos+jsin, or atan2 and Approximation method as CORDIC. Specify whether to map the blocks in your design to MAX, Min, CUSTOM, or ZERO latency for fixed-point and floating-point types. The default is MAX. See also LatencyStrategy (HDL Coder).
CustomLatency	To enable this property for fixed-point types, set Function as sin, cos, sincos, cos+jsin, or atan2 and Approximation method as CORDIC. When LatencyStrategy is set to CUSTOM, use this property to specify a custom latency value between ZERO and MAX for fixed-point types. See also LatencyStrategy (HDL Coder).

Native Floating Point
InputRangeReduction	Use this property for the sin, cos, sincos, cos+jsin, and atan2 functions. If your input range is unbounded, enable this property for HDL Coder to insert additional logic to reduce the range of inputs to [-pi, pi]. See also InputRangeReduction (HDL Coder).
HandleDenormals	Specify whether you want HDL Coder to insert additional logic to handle denormal numbers in your design. Denormal numbers are numbers that have magnitudes less than the smallest floating-point number that can be represented without leading zeros in the mantissa. The default is inherit. See also HandleDenormals (HDL Coder).
LatencyStrategy	Specify whether to map the blocks in your design to inherit, Max, Min, or Zero for the floating-point operator. The default is inherit. See also LatencyStrategy (HDL Coder).
MultiplyStrategy	Use this property for the sin, cos, sincos, cos+jsin, and atan2 functions. The default is inherit. Specify whether you want to use FullMultiplier or PartMultiplierPartAddShift. See also MantissaMultiplyStrategy (HDL Coder).

ULP Considerations

The Trigonometric Function blocks have nonzero units in the last place (ULP) error for floating point operations. For more information, see ULP Considerations of Native Floating-Point Operators (HDL Coder).

Restrictions

• For the sin and cos functions, the block supports only signed fixed-point data types are supported for CORDIC approximations.

• For functions that have the CORDIC mode, such as sin, cos, sincos, atan2, and cos+jsin, HDL code generation does not support fixed-point data types greater than 127 bits.

• For all the functions with Architecture set to Trigonometric, the block does not support double data types.

• HDL code generation does not support the lookup approximation method when:

  • The Interpolation method parameter is set to Linear point-slope and the Angle Unit parameter is set to radian or revolution.

  • The Interpolation method parameter is Flat and the Angle Unit parameter is radian.

• HDL Coder displays an error when a Trigonometric Function block is inside a feedback loop and you set:

  • Architecture to Cordic

  • UsePipelinedKernel to On

  The error occurs because the block is in a feedback loop and the code generator is unable to insert additional latency. To avoid this error, add a delay of length equal to the Number of iterations plus 3 adjacent to the block. The code generator then absorbs this delay to meet the additional latency of the Trigonometric Function block.

  For example, this Trigonometric Function block has Number of iterations set to 30. Adding a Delay block with a length 33 adjacent to the block meets the additional latency.

  

PLC Code Generation
Generate Structured Text code using Simulink® PLC Coder™.

Fixed-Point Conversion

Design and simulate fixed-point systems using Fixed-Point Designer™.

This block supports fixed-point and base integer data types when you set the Function to sin, cos, sincos, cos + jsin, or atan2 and set the Approximation method to CORDIC.

Version History

Introduced before R2006a