Entwurf eines LQG-Reglers

Als Beispiel für einen LQG-Entwurf soll das folgende Regelungsproblem dienen.

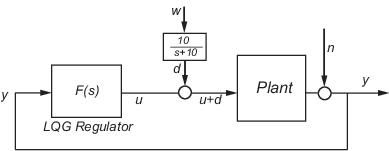
Das Ziel besteht darin, die Regelstreckenausgabe y um den Wert null zu regeln. Die Eingangsstörung d ist eine Störung niedriger Frequenz, deren spektrale Leistungsdichte (Power Spectral Density, PSD) sich unter 10 rad/s konzentriert. Für LQG-Entwurfszwecke wird sie als weißes Rauschen modelliert, das einen Tiefpassfilter mit einer Begrenzung bei 10 rad/s ansteuert, wie in der folgenden Abbildung dargestellt.

Der Einfachheit halber wird dieses Rauschen als Gaußsches weißes Rauschen mit der Varianz 1 modelliert.

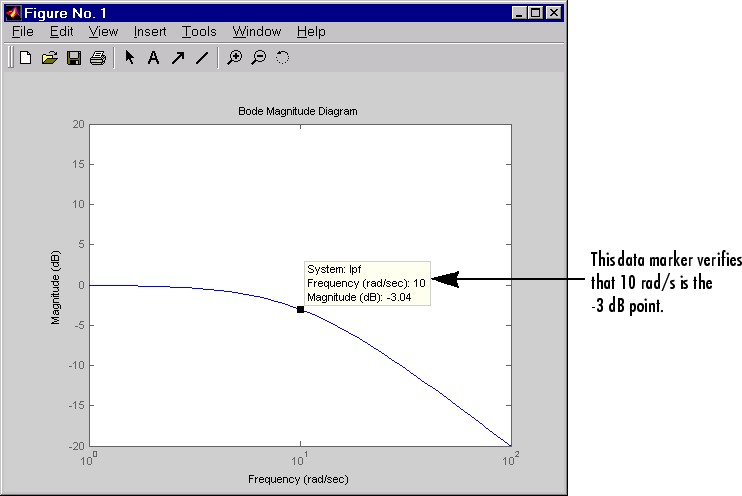
Die folgende Abbildung zeigt die Bode-Magnitude des Formfilters.

Bode-Magnitude des Tiefpassfilters

Es gibt ein gewisses Messrauschen n, dessen Rauschintensität sich ergibt aus

$E (n^{2}) = 0.01$

Verwenden Sie die Aufwandsfunktion

$J (u) = \int_{0}^{\infty} (10 y^{2} + u^{2}) d t$

um den Kompromiss zwischen Regelungsleistung und Steuerungsaufwand anzugeben. Die folgenden Gleichungen stellen das Zustandsraummodell eines offenen Regelkreises dar:

$\begin{array}{l} \dot{x} = A x + B u + B d (s t a t e e q u a t i o n s) \\ y = C x + n (m e a s u r e m e n t s) \end{array}$

Dabei gilt: (A,B,C) ist eine Zustandsraumrealisierung von $100 / (s^{2} + s + 100)$ .

Mit den folgenden Befehlen wird der optimale LQG-Regler F(s) für dieses Problem entworfen:

sys = ss(tf(100,[1 1 100])) % State-space plant model

% Design LQ-optimal gain K
K = lqry(sys,10,1)	 % u = -Kx minimizes J(u)

% Separate control input u and disturbance input d
P = sys(:,[1 1]);
% input [u;d], output y

% Design Kalman state estimator Kest.
Kest = kalman(P,1,0.01)

% Form LQG regulator = LQ gain + Kalman filter.
F = lqgreg(Kest,K)

Diese Befehle geben das Zustandsraummodell F des LQG-Reglers F(s) zurück. Die Funktionen lqry, kalman und lqgreg führen einen zeitdiskreten LQG-Entwurf durch, wenn Sie sie auf diskrete Regelstrecken anwenden.

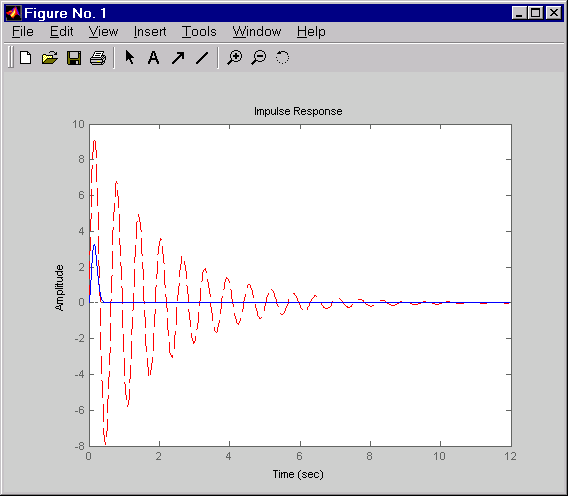
Um den Entwurf zu validieren, schließen Sie mit feedback die Schleife, erstellen einen Tiefpassfilter und fügen ihn in Reihenschaltung zum geschlossenen Regelkreis ein und verwenden dann die Funktion impulse, um die Impulsantworten des offenen und des geschlossenen Regelkreises zu vergleichen.

% Close loop
clsys = feedback(sys,F,+1)
% Note positive feedback.

% Create the lowpass filter and add it in series with clsys.
s = tf('s');
lpf= 10/(s+10) ;
clsys_fin = lpf*clsys;

% Open- vs. closed-loop impulse responses
impulse(sys,'r--',clsys_fin,'b-')

Diese Befehle erzeugen die folgende Abbildung, in der die Impulsantworten des offenen und des geschlossenen Regelkreises für dieses Beispiel verglichen werden.

Vergleich der Impulsantworten des offenen und des geschlossenen Regelkreises

Siehe auch

kalman | lqgreg

Entwurf eines LQG-Reglers

Siehe auch

Verwandte Themen