Kalman-Filterung

Dieses Beispiel demonstriert die Kalman-Filterung. Zunächst entwerfen Sie mithilfe des Befehls kalman einen Steady-State-Filter. Daraufhin simulieren Sie das System, um zu zeigen, wie der Filter den Fehler aufgrund von Messrauschen reduziert. Dieses Beispiel demonstriert zudem die Implementierung eines zeitvarianten Filters, der bei Systemen mit nicht stationären Rauschquellen nützlich sein kann.

Steady-State-Kalman-Filter

Betrachten Sie die folgenden diskrete Regelstrecke mit gaußschem Rauschen w am Eingang und Messrauschen v am Ausgang:

$$\begin{array}{c}x\left[n+1\right]=Ax\left[n\right]+Bu\left[n\right]+Gw\left[n\right]\\ y\left[n\right]=Cx\left[n\right]+Du\left[n\right]+Hw\left[n\right]+v\left[n\right]\end{array}$$

Das Ziel ist es, einen Kalman-Filter zur Schätzung des tatsächlichen Regelstrecken-Ausgangs ${\mathit{y}}_{\mathit{t}}\left[\mathit{n}\right]=\mathit{y}\left[\mathit{n}\right]-\mathit{v}\left[\mathit{n}\right]$ auf Grundlage der rauschbehafteten Messungen $\mathit{y}\left[\mathit{n}\right]$ zu entwickeln. Dieser Steady-State-Kalman-Filter verwendet für diese Schätzung die folgenden Gleichungen.

Zeitaktualisierung:

$\hat{\mathit{x}}\left[\mathit{n}+1|\mathit{n}\right]=\mathit{A}\hat{\mathit{x}}\left[\mathit{n}|\mathit{n}-1\right]+\mathit{Bu}\left[\mathit{n}\right]+\mathit{Gw}\left[\mathit{n}\right]$

Messungsaktualisierung:

$$\begin{array}{l}\underset{}{\overset{ˆ}{x}}\left[n|n\right]=\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]+M_x\left(y\left[n\right]-C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]-Du\left[n\right]\right)\\ \underset{}{\overset{ˆ}{y}}\left[n|n\right]=C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]+Du\left[n\right]+M_y\left(y\left[n\right]-C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]-Du\left[n\right]\right)\end{array}$$

Dabei gilt:

• $\hat{\mathit{x}}\left[\mathit{n}|\mathit{n}-1\right]$ ist die Schätzung von $\mathit{x}\left[\mathit{n}\right]$, angesichts früherer Messungen von bis zu $\mathit{y}\left[\mathit{n}-1\right]$.

• $\hat{\mathit{x}}\left[\mathit{n}|\mathit{n}\right]$ und$\hat{\mathit{y}}\left[\mathit{n}|\mathit{n}\right]$ sind die geschätzten Zustandswerte und die Messung, aktualisiert auf Basis der letzten Messung $\mathit{y}\left[\mathit{n}\right]$

• ${\mathit{M}}_{\mathit{x}}$ und ${\mathit{M}}_{\mathit{y}}$ sind die optimalen Innovations-Verstärkungsfaktoren, ausgewählt, um die Steady-State-Kovarianz des Schätzfehlers zu minimieren, auf Basis der Rauschen-Kovarianzen $\mathit{E}\left(\mathit{w}\left[\mathit{n}\right]{\mathit{w}\left[\mathit{n}\right]}^{\mathit{T}}\right)=\mathit{Q}$, $\mathit{E}\left(\mathit{v}\left[\mathit{n}\right]{\mathit{v}\left[\mathit{n}\right]}^{\mathit{T}}\right)=\mathit{R}$ und $\mathit{N}=\mathit{E}\left(\mathit{w}\left[\mathit{n}\right]{\mathit{v}\left[\mathit{n}\right]}^{\mathit{T}}\right)=0$. (Weitere Informationen zur Auswahl dieser Verstärkungsfaktoren finden Sie unter kalman.)

(Diese Aktualisierungsgleichungen beschreiben einen Schätzer vom Typ current. Weitere Informationen zum Unterschied zwischen current-Schätzern und delayed-Schätzern finden Sie unter kalman.)

Entwickeln des Filters

Sie können die kalman-Funktion zur Entwicklung dieses Steady-State-Kalman-Filters verwenden. Diese Funktion ermittelt den optimalen Steady-State-Filter-Verstärkungsfaktor M für eine bestimmte Regelstrecke, basierend auf der von Ihnen bereitgestellten Prozessrauschen-Kovarianz Q und der Sensorrauschen-Kovarianz R. Verwenden Sie bei diesem Beispiel die folgenden Werte für die Zustandsraum-Matrizen der Regelstrecke.

A = [1.1269   -0.4940    0.1129 
     1.0000         0         0 
          0    1.0000         0];

B = [-0.3832
      0.5919
      0.5191];

C = [1 0 0];

D = 0;

Setzen Sie in diesem Beispiel $\mathit{G}=\mathit{B}$, was bedeutet, dass das Prozessrauschen w additives Eingangsrauschen ist. Setzen Sie zudem $\mathit{H}=0$, was bedeutet, dass das Eingangsrauschen w keine direkte Auswirkung auf den Ausgang y hat. Diese Annahmen ergeben ein einfacheres Regelstreckenmodell:

$$\begin{array}{c}x\left[n+1\right]=Ax\left[n\right]+Bu\left[n\right]+Bw\left[n\right]\\ y\left[n\right]=Cx\left[n\right]+v\left[n\right]\end{array}$$

Wenn H = 0, kann gezeigt werden, dass ${\mathit{M}}_{\mathit{y}}=\mathit{C}{\mathit{M}}_{\mathit{x}}$ (siehe kalman). Zusammen vereinfachen diese Annahmen zudem die Aktualisierungsgleichungen für den Kalman-Filter.

Zeitaktualisierung:

$\hat{\mathit{x}}\left[\mathit{n}+1|\mathit{n}\right]=\mathit{A}\hat{\mathit{x}}\left[\mathit{n}|\mathit{n}-1\right]+\mathit{Bu}\left[\mathit{n}\right]+\mathit{Bw}\left[\mathit{n}\right]$

Messungsaktualisierung:

$$\begin{array}{l}\underset{}{\overset{ˆ}{x}}\left[n|n\right]=\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]+M_x\left(y\left[n\right]-C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]\right)\\ \underset{}{\overset{ˆ}{y}}\left[n|n\right]=C\underset{}{\overset{ˆ}{x}}\left[n|n\right]\end{array}$$

Um diesen Filter zu entwickeln, erstellen Sie zunächst das Regelstreckenmodell mit einem Eingang für w. Setzen Sie die Abtastzeit auf -1, um die Regelstrecke als diskret (ohne spezifische Abtastzeit) zu kennzeichnen.

Ts = -1;
sys = ss(A,[B B],C,D,Ts,'InputName',{'u' 'w'},'OutputName','y');  % Plant dynamics and additive input noise w

Die Prozessrauschen-Kovarianz Q und die Sensorrauschen-Kovarianz R sind Werte über Null, die Sie üblicherweise über Untersuchungen oder Messungen Ihres Systems erhalten. Legen Sie in diesem Beispiel die folgenden Werte fest.

Q = 2.3; 
R = 1; 

Verwenden Sie den Befehl kalman, um den Filter zu entwickeln.

[kalmf,L,~,Mx,Z] = kalman(sys,Q,R);

Dieser Befehl entwickelt den Kalman-Filter kalmf, ein Zustandsraummodell, das die Gleichungen für die Aktualisierung von Zeit und Messungen implementiert. Die Filtereingänge sind der Regelstrecken-Eingang u und der rauschbehaftete Regelstrecken-Ausgang y. Der erste Ausgang von kalmf ist die Schätzung $\hat{\mathit{y}}$ des tatsächlichen Regelstrecken-Ausgangs, die verbleibenden Ausgänge sind die Zustandsschätzungen $\hat{\mathit{x}}$.

Verwerfen Sie für dieses Beispiel die Zustandsschätzungen und behalten Sie nur den ersten Ausgang $\hat{\mathit{y}}$.

kalmf = kalmf(1,:);

Verwenden des Filters

Um die Funktionsweise dieses Filters zu betrachten, generieren Sie Daten und vergleichen Sie die gefilterte Antwort mit der tatsächlichen Regelstreckenantwort. Das vollständige System ist im folgenden Diagramm dargestellt.

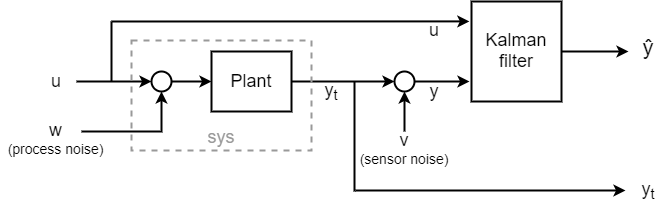
Um dieses System zu simulieren und einen Eingang für das Messrauschen v zu erstellen, verwenden Sie einen sumblk. Verwenden Sie daraufhin connect, um sys und den Kalman-Filter miteinander zu verbinden, sodass u ein gemeinsamer Eingang ist und der rauschbehaftete Regelstrecken-Ausgang y dem anderen Filtereingang übergeben wird. Das Ergebnis ist ein Simulationsmodell mit den Eingängen w, v und u sowie den Ausgängen yt (tatsächliche Antwort) und ye (gefilterte oder geschätzte Antwort $\hat{\mathit{y}}$). Die Signale yt und ye sind die Ausgänge der Regelstrecke bzw. des Filters.

sys.InputName = {'u','w'};
sys.OutputName = {'yt'};
vIn = sumblk('y=yt+v');

kalmf.InputName = {'u','y'};
kalmf.OutputName = 'ye';

SimModel = connect(sys,vIn,kalmf,{'u','w','v'},{'yt','ye'});

Um das Filterverhalten zu simulieren, generieren Sie einen bekannten sinusförmigen Eingangsvektor.

t = (0:100)';
u = sin(t/5);

Generieren Sie Prozess- und Sensor-Rauschvektoren mithilfe derselben Rauschen-Kovarianzwerte Q und R, die Sie beim Entwickeln des Filters verwendet haben.

rng(10,'twister');
w = sqrt(Q)*randn(length(t),1);
v = sqrt(R)*randn(length(t),1);

Simulieren Sie schließlich mit lsim die Antwort.

out = lsim(SimModel,[u,w,v]);

lsim generiert die Antwort bei den Ausgängen yt und ye gemäß den Eingängen an w, v und u. Extrahieren Sie die Kanäle yt und ye und berechnen Sie die gemessene Antwort.

yt = out(:,1);   % true response
ye = out(:,2);  % filtered response
y = yt + v;     % measured response

Vergleichen Sie die tatsächliche Antwort mit der gefilterten Antwort.

clf
subplot(211), plot(t,yt,'b',t,ye,'r--'), 
xlabel('Number of Samples'), ylabel('Output')
title('Kalman Filter Response')
legend('True','Filtered')
subplot(212), plot(t,yt-y,'g',t,yt-ye,'r--'),
xlabel('Number of Samples'), ylabel('Error')
legend('True - measured','True - filtered')

Wie das zweite Diagramm zeigt, reduziert der Kalman-Filter den Fehler yt - y aufgrund von Messungsrauschen. Um diese Reduktion zu bestätigen, berechnen Sie die Kovarianz des Fehlers vor der Filterung (Messfehler-Kovarianz) und nach der Filterung (Schätzfehler-Kovarianz).

MeasErr = yt - y;
MeasErrCov = sum(MeasErr.*MeasErr)/length(MeasErr)

MeasErrCov = 
0.9871

EstErr = yt - ye;
EstErrCov = sum(EstErr.*EstErr)/length(EstErr)

EstErrCov = 
0.3479

Entwurf eines zeitvarianten Kalman-Filters

Bei dem vorherigen Entwurf wurde davon ausgegangen, dass die Kovarianz des Rauschens sich über die Zeit hinweg nicht verändert. Ein zeitvarianter Kalman-Filter eignet sich gut für Situationen, in denen die Kovarianz des Rauschens nicht stationär ist.

Der zeitvariante Kalman-Filter weist die folgenden Aktualisierungsgleichungen auf. Bei dem zeitvarianten Filter können sowohl die Fehler-Kovarianz $\mathit{P}\left[\mathit{n}\right]$ als auch der Innovations-Verstärkungsfaktor ${\mathit{M}}_{\mathit{x}}\left[\mathit{n}\right]$ über die Zeit hinweg schwanken. Sie können die Gleichungen zur Aktualisierung von Zeit und Messungen folgendermaßen verändern, um die Zeitvariation zu berücksichtigen; auch hier wird $\mathit{G}=\mathit{B}$ verwendet, sodass das Prozessrauschen w additives Eingangsrauschen ist.

Zeitaktualisierung:

$$\begin{array}{l}\underset{}{\overset{ˆ}{x}}\left[n+1|n\right]=A\underset{}{\overset{ˆ}{x}}\left[n|n\right]+Bu\left[n\right]+Bw\left[n\right]\\ P\left[n+1|n\right]=AP\left[n|n\right]A^T+BQ{B}^T\end{array}$$

Messungsaktualisierung:

$$\begin{array}{l}\underset{}{\overset{ˆ}{x}}\left[n|n\right]=\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]+M_x\left[n\right]\left(y\left[n\right]-C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]\right)\\ M_x\left[n\right]=P\left[n|n-1\right]C^T{\left(CP\left[n|n-1\right]C^T+R\left[n\right]\right)}^{-1}\\ P\left[n|n\right]=\left(I-M_x\left[n\right]C\right)P\left[n|n-1\right]\\ \underset{}{\overset{ˆ}{y}}\left[n|n\right]=C\underset{}{\overset{ˆ}{x}}\left[n|n\right]\end{array}$$

Weitere Informationen zu diesen Ausdrücken finden Sie unter kalman.

In Simulink® können Sie einen zeitvarianten Kalman-Filter mithilfe des Kalman Filter-Blocks implementieren (siehe State Estimation Using Time-Varying Kalman Filter).

Um einen zeitvarianten Kalman-Filter in MATLAB® zu erstellen, generieren Sie zunächst die rauschbehaftete Regelstreckenantwort. Simulieren Sie die Regelstreckenantwort auf das Eingangssignal u und das Prozessrauschen w, die zuvor definiert wurden. Addieren Sie daraufhin das Messrauschen v zur simulierten tatsächlichen Antwort yt hinzu, um die rauschbehaftete Antwort y zu erhalten. In diesem Beispiel ändern sich die Kovarianzen der Rauschvektoren w und v nicht mit der Zeit. Sie können jedoch dasselbe Verfahren für nicht stationäres Rauschen verwenden.

yt = lsim(sys,[u w]);   
y = yt + v;         

Implementieren Sie daraufhin die rekursiven Gleichungen für die Filter-Aktualisierung in einer for-Schleife.

P = B*Q*B';         % Initial error covariance
x = zeros(3,1);     % Initial condition on the state

ye = zeros(length(t),1);
ycov = zeros(length(t),1); 
errcov = zeros(length(t),1); 

for i=1:length(t)
  % Measurement update
  Mxn = P*C'/(C*P*C'+R);
  x = x + Mxn*(y(i)-C*x);   % x[n|n]
  P = (eye(3)-Mxn*C)*P;     % P[n|n]

  ye(i) = C*x;
  errcov(i) = C*P*C';

  % Time update
  x = A*x + B*u(i);        % x[n+1|n]
  P = A*P*A' + B*Q*B';     % P[n+1|n] 
end

Vergleichen Sie die tatsächliche Antwort mit der gefilterten Antwort.

subplot(211), plot(t,yt,'b',t,ye,'r--')
xlabel('Number of Samples'), ylabel('Output')
title('Response with Time-Varying Kalman Filter')
legend('True','Filtered')
subplot(212), plot(t,yt-y,'g',t,yt-ye,'r--'),
xlabel('Number of Samples'), ylabel('Error')
legend('True - measured','True - filtered')

Der zeitvariante Filter schätzt während der Schätzung zudem die Ausgangs-Kovarianz. Da dieses Beispiel ein stationäres Eingangsrauschen verwendet, tendiert die Ausgangs-Kovarianz zu einem Steady-State-Wert hin. Plotten Sie die Ausgangs-Kovarianz, um zu bestätigen, dass der Filter einen Steady State erreicht hat.

figure
plot(t,errcov) 
xlabel('Number of Samples'), ylabel('Error Covariance'),

Im Kovarianz-Diagramm können Sie sehen, dass die Ausgangs-Kovarianz bei etwa fünf Abtastungen einen Steady State erreicht hat. Daraufhin weist der zeitvariante Filter dieselbe Leistung auf wie die Steady-State-Version.

Wie bei dem Steady-State-Fall reduziert der Filter den Fehler aufgrund Messrauschen. Um diese Reduktion zu bestätigen, berechnen Sie die Kovarianz des Fehlers vor der Filterung (Messfehler-Kovarianz) und nach der Filterung (Schätzfehler-Kovarianz).

MeasErr = yt - y;
MeasErrCov = sum(MeasErr.*MeasErr)/length(MeasErr)

MeasErrCov = 
0.9871

EstErr = yt - ye;
EstErrCov = sum(EstErr.*EstErr)/length(EstErr)

EstErrCov = 
0.3479

Wenn der zeitvariante Filter schließlich den Steady State erreicht, entsprechen die Werte der Verstärkungsmatrix Mxn den von kalman für den Steady-State-Filter berechneten Werten.

Mx,Mxn

Mx = 3×1

    0.5345
    0.0101
   -0.4776

Mxn = 3×1

    0.5345
    0.0101
   -0.4776

Mehr über Kalman-Filter erfahren

Weitere Informationen über Kalman-Filter finden Sie in diesem Video oder dem Rest der Serie unter Understanding Kalman Filters — MATLAB Tech Talks.

Video-Transkript

Siehe auch

kalman

Themen

• State Estimation Using Time-Varying Kalman Filter
• LQG Regulation: Rolling Mill Case Study

Externe Websites

• Kalman-Filter verstehen – MATLAB-Videoreihe