jacobiCD
Jacobi CD elliptic function
Syntax
Description
jacobiCD(
returns the Jacobi CD Elliptic Function of
u,m)u and m. If u or
m is an array, then jacobiCD acts
element-wise.
Examples
Calculate Jacobi CD Elliptic Function for Numeric Inputs
jacobiCD(2,1)
ans =
1Call jacobiCD on array inputs.
jacobiCD acts element-wise when
u or m is an array.
jacobiCD([2 1 -3],[1 2 3])
ans =
1.0000 2.3829 -178.6290Calculate Jacobi CD Elliptic Function for Symbolic Numbers
Convert numeric input to symbolic form using
sym, and find the Jacobi CD elliptic function. For
symbolic input where u = 0 or m = 0 or
1, jacobiCD returns exact symbolic
output.
jacobiCD(sym(2),sym(1))
ans = 1
Show that for other values of u or
m, jacobiCD returns an unevaluated
function call.
jacobiCD(sym(2),sym(3))
ans = jacobiCD(2, 3)
Find Jacobi CD Elliptic Function for Symbolic Variables or Expressions
For symbolic variables or expressions,
jacobiCD returns the unevaluated function call.
syms x y f = jacobiCD(x,y)
f = jacobiCD(x, y)
Substitute values for the variables by using subs, and
convert values to double by using double.
f = subs(f, [x y], [3 5])
f = jacobiCD(3, 5)
fVal = double(f)
fVal =
1.0019Calculate f to higher precision using
vpa.
fVal = vpa(f)
fVal = 1.0019475527333315357888731083364
Plot Jacobi CD Elliptic Function
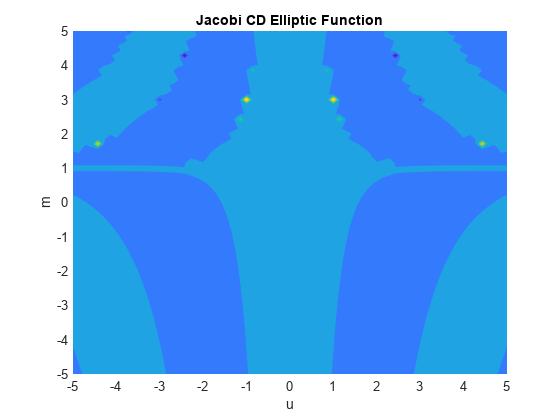
Plot the Jacobi CD elliptic function using fcontour. Set u on the x-axis and m on the y-axis by using the symbolic function f with the variable order (u,m). Fill plot contours by setting Fill to on.
syms f(u,m) f(u,m) = jacobiCD(u,m); fcontour(f,'Fill','on') title('Jacobi CD Elliptic Function') xlabel('u') ylabel('m')
Input Arguments
u — Input
number | vector | matrix | multidimensional array | symbolic number | symbolic variable | symbolic vector | symbolic matrix | symbolic multidimensional array | symbolic function | symbolic expression
Input, specified as a number, vector, matrix, or multidimensional array, or a symbolic number, variable, vector, matrix, multidimensional array, function, or expression.
m — Input
number | vector | matrix | multidimensional array | symbolic number | symbolic variable | symbolic vector | symbolic matrix | symbolic multidimensional array | symbolic function | symbolic expression
Input, specified as a number, vector, matrix, or multidimensional array, or a symbolic number, variable, vector, matrix, multidimensional array, function, or expression.
More About
Jacobi CD Elliptic Function
The Jacobi CD elliptic function is
cd(u,m) = cn(u,m)/dn(u,m)
where cn and dn are the respective Jacobi elliptic functions.
The Jacobi elliptic functions are meromorphic and doubly periodic in their first
argument with periods 4K(m) and 4iK'(m), where K is the complete elliptic integral of the first kind, implemented
as ellipticK.
Version History
Introduced in R2017b
MATLAB-Befehl
Sie haben auf einen Link geklickt, der diesem MATLAB-Befehl entspricht:
Führen Sie den Befehl durch Eingabe in das MATLAB-Befehlsfenster aus. Webbrowser unterstützen keine MATLAB-Befehle.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)