Internal Delays
Using the InputDelay, OutputDelay,
and ioDelay properties, you can model simple processes
with transport delays. However, these properties cannot model more
complex situations, such as feedback loops with delays. In addition
to the InputDelay and OutputDelay properties,
state-space (ss) models have an InternalDelay property.
This property lets you model the interconnection of systems with input,
output, or transport delays, including feedback loops with delays.
You can use InternalDelay property to accurately
model and analyze arbitrary linear systems with delays. Internal delays
can arise from the following:
Concatenating state-space models with input and output delays.
Feeding back a delayed signal.
Converting MIMO
tforzpkmodels with transport delays to state-space form.
Using internal time delays, you can do the following:
In continuous time, generate approximate-free time and frequency simulations, because delays do not have to be replaced by a Padé approximation. In continuous time, this allows for more accurate analysis of systems with long delays.
In discrete time, keep delays separate from other system dynamics, because delays are not replaced with poles at z = 0, which boosts efficiency of time and frequency simulations for discrete-time systems with long delays.
Use most Control System Toolbox™ functions.
Test advanced control strategies for delayed systems. For example, you can implement and test an accurate model of a Smith predictor. See the example Control of Processes with Long Dead Time: The Smith Predictor.
Why Internal Delays Are Necessary
This example illustrates why input, output, and transport delays not enough to model all types of delays that can arise in dynamic systems. Consider the simple feedback loop with a 2 s. delay:
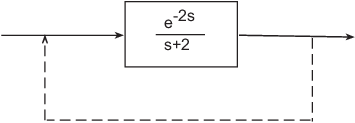
The closed-loop transfer function is
The delay term in the numerator can be represented as an output
delay. However, the delay term in the denominator cannot. In order
to model the effect of the delay on the feedback loop, the InternalDelay property
is needed to keep track of internal coupling between delays and ordinary
dynamics.
Typically, you do not create state-space models with internal delays directly, by specifying the A, B, C, and D matrices together with a set of internal delays. Rather, such models arise when you interconnect models having delays. There is no limitation on how many delays are involved and how the models are connected. For an example of creating an internal delay by closing a feedback loop, see Closing Feedback Loops with Time Delays.
Behavior of Models With Internal Delays
When you work with models having internal delays, be aware of the following behavior:
When a model interconnection gives rise to internal delays, the software returns an
ssmodel regardless of the interconnected model types. This occurs because onlysssupports internal delays.The software fully supports feedback loops. You can wrap a feedback loop around any system with delays.
When displaying the
A,B,C, andDmatrices, the software sets all delays to zero (creating a zero-order Padé approximation). This approximation occurs for the display only, and not for calculations using the model.For some systems, setting delays to zero creates singular algebraic loops, which result in either improper or ill-defined, zero-delay approximations. For these systems:
Entering
sysreturns only sizes for the matrices of a system namedsys.Entering
sys.Aproduces an error.The limited display and the error do not imply a problem with the model
sysitself.
Inside Time Delay Models
State-space objects use generalized state-space equations to keep track of internal delays. Conceptually, such models consist of two interconnected parts:
An ordinary state-space model H(s) with an augmented I/O set
A bank of internal delays.
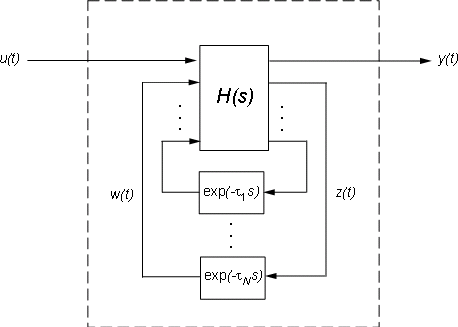
The corresponding state-space equations are:
You need not bother with this internal representation to use
the tools. If, however, you want to extract H or
the matrices A, B1, B2, ... ,
you can use getDelayModel,
For the example:
P = 5*exp(-3.4*s)/(s+1); C = 0.1 * (1 + 1/(5*s)); T = feedback(ss(P*C),1); [H,tau] = getDelayModel(T,'lft'); size(H)
Note that H is a two-input, two-output model
whereas T is SISO. The inverse operation (combining H and tau to
construct T) is performed by setDelayModel.
Functions That Support Internal Time Delays
The following commands support internal delays for both continuous- and discrete-time systems:
Limitations on Functions that Support Internal Time Delays
The following commands support internal delays for both continuous- and discrete-time systems and have certain limitations:
allmargin,margin—Uses interpolation, therefore these commands are only as precise as the fineness of the specified grid.pole,zero—Returns poles and zeros of the system with all delays set to zero.ssdata,get—If an SS model has internal delays, these commands return theA,B,C, andDmatrices of the system with all internal delays set to zero. UsegetDelayModelto access the internal state-space representation of models with internal delays.
Functions That Do Not Support Internal Time Delays
The following commands do not support internal time delays:
References
[1] P. Gahinet and L.F. Shampine, "Software for Modeling and Analysis of Linear Systems with Delays," Proc. American Control Conf., Boston, 2004, pp. 5600-5605
[2] L.F. Shampine and P. Gahinet, Delay-differential-algebraic Equations in Control Theory, Applied Numerical Mathematics, 56 (2006), pp. 574-588