LPV System

Simulation von linearen parametervarianten Systemen (LPV-Systemen)

• 

Bibliotheken:
Control System Toolbox / Linear Parameter Varying

Beschreibung

Ein lineares parametervariantes (LPV) System ist ein lineares Zustandsraummodell, dessen Dynamik in Abhängigkeit bestimmter zeitlich variabler Parameter, der sogenannten Planungsparameter, variiert. In MATLAB^® wird ein LPV-Modell in Form eines Zustandsraums mit Koeffizienten dargestellt, die von den Parametern abhängig sind.

Mathematisch können Sie ein LPV-System folgendermaßen darstellen.

$$\begin{array}{l}dx\left(t\right)=d{x}_0(p)+A\left(p\right)\left(x\left(t\right)-x_0\left(p\right)\right)+B\left(p\right)\left(u\left(t\right)-u_0(p)\right)\\ y\left(t\right)=y_0\left(p\right)+C\left(p\right)\left(x\left(t\right)-x_0\left(p\right)\right)+D\left(p\right)\left(u\left(t\right)-u_0(p)\right)\\ x\left(0\right)=x_{init}\end{array}$$

Dabei gilt:

• u(t) sind die Eingänge

• y(t) sind die Ausgänge

• x(t) sind die Modellzustände mit Anfangswert x_init

• $dx\left(t\right)$ ist der Vektor der Zustandsableitung $\dot{x}$ für zeitkontinuierliche Systeme und der Vektor der Zustandsaktualisierung x[k+1] für zeitdiskrete Systeme. Hier ist k der Integer-Index, der die Anzahl Abtastperioden T_s zählt.

• A(p), B(p), C(p) und D(p) sind die Zustandsraum-Matrizen, die durch den Planungsparameter-Vektor p festgelegt sind.

• Die Parameter p = p(t) sind messbare Funktionen der Eingänge und der Zustände des Modells. Sie können eine skalare Größe oder ein Vektor aus mehreren Parametern sein. Die Menge der Planungsparameter definiert den Planungsraum, auf dem das LPV-Modell definiert ist.

• dx₀(p), x₀(p), u₀(p) und y₀(p) sind die Offets der Werte von $dx\left(t\right)$, x(t), u(t) und y(t) bei einem bestimmten Parameterwert p = p(t) oder p[k].

  Sie können die Offsets erhalten, indem Sie zusätzliche Linearisierungsinformationen zurückliefern, wenn Sie Funktionen wie linearize (Simulink Control Design) oder getIOTransfer (Simulink Control Design) aufrufen. Ein Beispiel hierzu finden Sie unter LPV Approximation of Boost Converter Model (Simulink Control Design).

Vorsicht

Vermeiden Sie es, C(p) und D(p) von den Systemausgängen y abhängig zu machen. Andernfalls führt die resultierende Zustandsraumgleichung y = C(y)x + D(y)u zu einer algebraischen Schleife, da die Berechnung des Ausgangswerts y die Kenntnis des Ausgangswerts voraussetzt. Diese algebraische Schleife neigt zu Instabilität und Divergenz. Versuchen Sie stattdessen, C und D in Form der Zeit t, der Blockeingänge u und der Zustandsausgänge x auszudrücken.

Aus ähnlichen Gründen gilt es zu vermeiden, A(p) und B(p) auf der Grundlage des dx-Ausgangs zu planen. Beachten Sie, dass A und B ohne Weiteres von y abhängen dürfen, wenn y eine feste Kombination von Zuständen und Eingängen ist (mit anderen Worten, wenn y = Cx + Du, wobei C und D konstante Matrizen sind).

Der Block implementiert eine gitterbasierte Darstellung des LPV-Systems. Der Nutzer wählt ein Wertegitter für die Planungsparameter. Für jeden Wert p = p* geben Sie das entsprechende lineare System als ein Zustandsraum-Modellobjekt (ss oder idss (System Identification Toolbox)) an. Sie verwenden das generierte Array von Zustandsraummodellen, um den Block LPV System zu konfigurieren.

Der Block akzeptiert ein Array von Zustandsraummodellen mit Betriebspunktinformationen. Der Block extrahiert Informationen über die Planungsvariablen aus der Eigenschaft SamplingGrid des LTI-Arrays. Die Planungsvariablen definieren das Gitter der LPV-Modelle. Sie sind skalarwertige Größen, die Funktionen der Zeit, Eingänge und Zustände oder Konstanten sein können. Sie werden verwendet, um die lokale Dynamik im Betriebsbereich zu bestimmen. Die Software interpoliert die Werte dieser Variablen. Der Block verwendet dieses Array mit Dateninterpolations- und Extrapolationstechniken für die Simulation.

Beispiele

Konfigurieren des Eingangs-Ports der Planungsparameter

Betrachten Sie ein LPV-Modell mit 2 Eingängen, 3 Ausgängen und 4 Zuständen. Verwenden Sie den Eingang u(2) und den Zustand x(1) als Planungsparameter. Konfigurieren Sie das Simulink^®-Modell wie in der folgenden Abbildung gezeigt.

Simulieren linearer parametervarianter Systeme mit dem LPV System-Block

Betrachten Sie ein lineares Masse-Feder-Dämpfer-System, dessen Masse sich in Abhängigkeit von einer externen Laststeuerung ändert. Die maßgebliche Gleichung lautet:

$$\mathit{m}\left(\mathit{u}\right)\ddot{\mathit{y}}+\mathit{c}\dot{\mathit{y}}+\mathit{ky}=\mathit{F}\left(\mathit{t}\right)$$

Wobei $\mathit{m}\left(\mathit{u}\right)$ die von der externen Steuerung $\mathit{u}$ abhängige Masse, $\mathit{c}$ das Dämpfungsverhältnis, $\mathit{k}$ die Steifigkeit der Feder und $\mathit{F}\left(\mathit{t}\right)$ die Antriebskraft ist. $\mathit{y}\left(\mathit{t}\right)$ ist die Position der Masse zu einem bestimmten Zeitpunkt $\mathit{t}$. Für einen festen Wert von $\mathit{u}$ ist das System linear und lässt sich wie folgt ausdrücken

$$\mathit{A}=\left[\begin{array}{cc}0& 1\\ -\frac{\mathit{k}}{\mathit{m}}& -\frac{\mathit{c}}{\mathit{m}}\end{array}\right],$$

$$\mathit{B}=\left[\begin{array}{c}0\\ \frac{1}{\mathit{m}}\end{array}\right],$$

$$\mathit{C}=\left[\begin{array}{cc}1& 0\end{array}\right]$$

$$\begin{array}{l}\dot{\mathit{x}}=\mathit{Ax}+\mathit{Bu}\\ \mathit{y}=\mathit{Cx}\end{array}$$,

Dabei gilt: $\mathit{x}=\left[\begin{array}{c}\mathit{y}\\ \dot{\mathit{y}}\end{array}\right]$ ist der Zustandsvektor und $\mathit{m}$ der Wert der Masse für einen bestimmten Wert von $\mathit{u}$.

In diesem Beispiel geht es darum, das Verhalten des Modells über einen Bereich von Eingangswerten von 1 bis 10 Volt zu untersuchen. Messen Sie für jeden Wert von $\mathit{u}$ die Masse und berechnen Sie die lineare Darstellung des Systems. Nehmen Sie an, die Masse ist mit dem Eingang durch die folgende Beziehung verbunden: $\mathit{m}\left(\mathit{u}\right)=10\mathit{u}+0.1{\mathit{u}}^2$. Für Werte von u im Bereich von 1 bis 10 ergibt sich das folgende Array linearer Systeme.

c = 5;   
k = 300; 
u = 1:10;
m = 10*u + 0.1*u.^2;
for i = 1:length(u)
   A = [0 1; -k/m(i), -c/m(i)];
   B = [0; 1/m(i)];
   C = [1 0];
   sys(:,:,i) = ss(A,B,C,0); 
end

Die Variable $\mathit{u}$ ist der Planungseingang. Fügen Sie diese Information dem Modell hinzu.

sys.SamplingGrid = struct('LoadCommand',u);

Konfigurieren des LPV-System-Blocks:

• Geben Sie sys in das Feld Zustandsraum-Array ein.

• Verbinden Sie den Eingangs-Port par mit einem eindimensionalen Quellsignal, das die Werte der Laststeuerung erzeugt. Wenn die Quelle Werte zwischen 1 und 10 liefert, verwendet der Block Interpolation zur Berechnung des linearen Modells zu einem bestimmten Zeitpunkt.. Andernfalls verwendet der Block Extrapolation.

Simulieren Sie das LPV-Modell mit einem konstanten Krafteingang von 100 N und zufälligen Werten für die Lastbefehl-Planungsvariable.

model = "simMSDLPV";
open_system(model);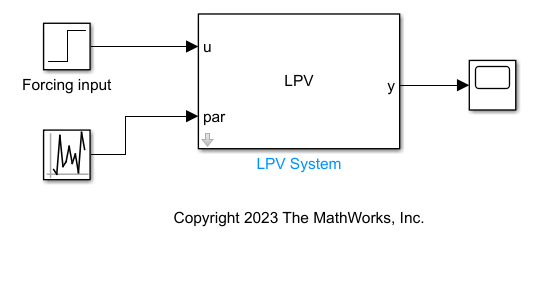

Vergleichen der nicht linearen Modellantwort und LPV Block-Antwort

Dieses Beispiel demonstriert, wie Sie ein lineares parametervariantes Modell (LPV) einer Motordrehzahl mit dem LPV System-Block simulieren können. Der LPV System-Block interpoliert ein Zustandsraum-Array, um die LPV-Antwort zu modellieren. Üblicherweise erstellen Sie ein derartiges Array, indem Sie ein nicht lineares Modell über einen Bereich von Betriebsbedingungen hinweg im Batch linearisieren. Dieses Beispiel umfasst ein linearisiertes Ergebnis des Motordrehzahlmodells in scdspeedlpvData. Weitere Informationen zur Linearisierung dieses Modells finden Sie unter Linearize Engine Speed Model (Simulink Control Design).

Öffnen Sie das Modell.

model = "scdspeedLPVCompare";
open_system(model);

Laden Sie das Linearisierungsergebnis zur Implementierung des LPV-Modells.

load scdspeedlpvData.mat

Das LPV-Modell wird im LPV Modell-Subsystem implementiert.

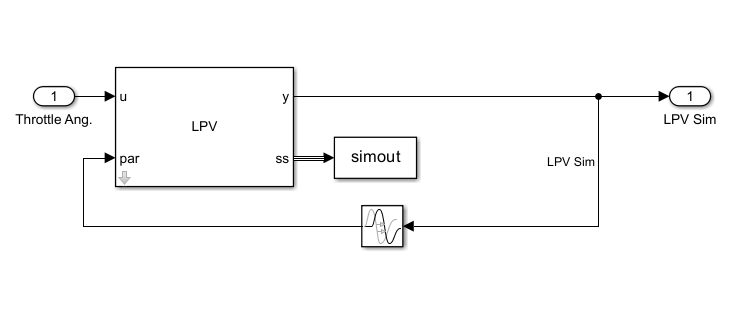
Der LPV System-Block verwendet die Drosselklappenstellung als Eingang und den Drehzahlausgang als Planungsvariable. Die Blockparameter werden wie in der Abbildung dargestellt konfiguriert. Hier erhalten Sie das Zustandsraum-Array sys und den Offset, indem Sie das nicht lineare Modelle im Batch linerarisieren.

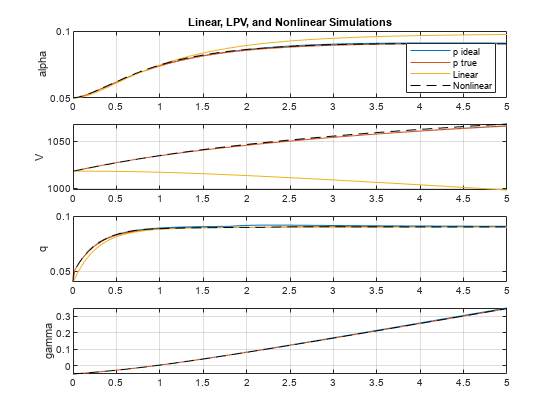
Simulieren Sie das Modell und plotten Sie den Antwortvergleich.

sim(model);
plot(logsOut{1}.Values.Time,logsOut{1}.Values.Data)
grid on
legend("Nonlinear sim","LPV sim","LTI sim",Location="best")

Das LPV-Modell stellt eine gute Annäherung der nicht linearen Antwort dar.

Erweiterte Beispiele

LPV Approximation of Boost Converter Model

Approximate a nonlinear Simscape™ Electrical™ model using a linear parameter varying model.

(Simulink Control Design)

Design and Validate Gain-Scheduled Controller for Nonlinear Aircraft Pitch Dynamics

Approximate nonlinear behavior of airframe pitch axis dynamics using linear parameter-varying model.

• Live Script öffnen

Using LTI Arrays for Simulating Multi-Mode Dynamics

Construct a Linear Parameter Varying (LPV) representation of a system that exhibits multi-mode dynamics.

• Script öffnen

Approximate Nonlinear Behavior Using Array of LTI Systems

You can use linear parameter varying models to approximate the dynamics of nonlinear systems.

(Simulink Control Design)

Beschränkungen

• Interne Verzögerungen können nicht so extrapoliert werden, dass sie kleiner sind als ihr Minimalwert im Zustandsraum-Modellarray.

• Wenn Sie ein Streuraster von linearen Modellen verwenden, um das LPV-System zu definieren, wird nur das Schema der Nächster-Nachbar-Interpolation verwendet. Dies kann die Genauigkeit der Simulationsergebnisse verringern. Es wird empfohlen, mit rechteckigen Rastern, die mit ndgrid erstellt wurden, zu arbeiten.

Ports

Eingänge

u — Eingangssignal

Skalar | Vektor

Geben Sie das Eingangssignal u(t) an. Bei mehreren Eingängen akzeptiert dieser Port ein Signal der Dimension des Eingangs.

par — Parameterwerte

Skalar | Vektor

Stellen Sie die Signale für die Variablen bereit, die den Planungsraum definieren (Abtastraster-Variablen). Die Planungsvariablen können Funktionen der Zeit, Eingänge und Zustände oder Konstanten sein. Die erforderliche Abhängigkeit kann erreicht werden, indem Sie ein Planungssignal mit Takteingang (für die Zeit), ein Eingangssignal (u) und die Ausgangszustandssignale (x) des LPV-Blocks oder exogene Signale, je nach Bedarf, vorbereiten.

Vorsicht

Vermeiden Sie es, C(p) und D(p) von den Systemausgängen y abhängig zu machen. Andernfalls führt die resultierende Zustandsraumgleichung y = C(y)x + D(y)u zu einer algebraischen Schleife, da die Berechnung des Ausgangswerts y die Kenntnis des Ausgangswerts voraussetzt. Diese algebraische Schleife neigt zu Instabilität und Divergenz. Versuchen Sie stattdessen, C und D in Form der Zeit t, der Blockeingänge u und der Zustandsausgänge x auszudrücken.

Aus ähnlichen Gründen gilt es zu vermeiden, A(p) und B(p) auf der Grundlage des dx-Ausgangs zu planen. Beachten Sie, dass A und B ohne Weiteres von y abhängen dürfen, wenn y eine feste Kombination von Zuständen und Eingängen ist (mit anderen Worten, wenn y = Cx + Du, wobei C und D konstante Matrizen sind).

IC — Anfangsbedingungen

Vektor

Seit R2024b

Anfangsbedingungen, die mit dem lokalen Modell zu verwenden sind, um die Simulation zu beginnen, angegeben als Vektor mit Länge gleich der Anzahl der Modellzustände.

Abhängigkeiten

Um diesen Port zu aktivieren, setzen Sie Initial condition source auf external.

Ausgänge

y — Modellausgänge

Skalar | Vektor

Antwort des linearen parametervarianten Modells.

x — Zustandswerte

Skalar | Vektor

Werte der Modellzustände.

Abhängigkeiten

Um diesen Port zu aktivieren, wählen Sie Output states auf der Registerkarte Outputs der Blockparameter aus.

dx — Zustandsableitungswerte

Skalar | Vektor

Werte der Zustandsableitungen. Die Zustandsableitungen werden manchmal verwendet, um die Planungsparameter zu definieren. Vermeiden Sie jedoch die Planung von A und B auf der Grundlage des dx-Ausgangs.

Abhängigkeiten

Um diesen Port zu aktivieren, wählen Sie Output state derivatives (continuous-time) or updates (discrete-time) auf der Registerkarte Outputs der Blockparameter aus.

ss — Lokales Zustandsraummodell

bus

Lokales Zustandsraummodell in den wichtigsten Simulationszeitschritten, ausgegeben als Bus-Signal mit den folgenden Elementen.

• A – Zustandsmatrix

• B – Eingangsmatrix

• C – Ausgangsmatrix

• D – Feedthrough-Matrix

• InputDelay – Eingangsverzögerung

• OutputDelay – Ausgangsverzögerung

• InternalDelay – Interne Verzögerungen im Modell

Abhängigkeiten

Um diesen Port zu aktivieren, wählen Sie Output interpolated state-space data auf der Registerkarte Outputs der Blockparameter aus.

offset — LPV-Modell-Offsets

bus

LPV-Modell-Offsetdaten in den wichtigsten Simulationszeitschritten, ausgegeben als Bus-Signal mit den folgenden Elementen.

• InputOffset

• OutputOffset

• StateOffset

• StateDerivativeOffset

Abhängigkeiten

Um diesen Port zu aktivieren, wählen Sie Output interpolated offsets auf der Registerkarte Outputs der Blockparameter aus.

Parameter

Verwenden Sie den Property Inspector, um die Blockparameter interaktiv zu bearbeiten. Wählen Sie in der Werkzeugleiste Simulink auf der Registerkarte Simulation in der Galerie Prepare Property Inspector aus.

Registerkarte LPV-Modell

State-space array — Array aus Zustandsraummodellen

Array aus ss- oder idss-Modellen

Ein Array von Zustandsraummodellen (ss oder idss (System Identification Toolbox)). Alle Modelle in dem Array müssen die gleiche Zustandsdefinition verwenden.

Das Zustandsraum-Array muss die Planungsparameter und das Interpolationsraster für das Modell in der Eigenschaft SamplingGrid festlegen. Sie können die Modell-Offsets in der Eigenschaft Offsets des Arrays angeben, wenn Sie den Parameter Operating Point Offsets auf Use offsets in state-space array setzen. Weitere Informationen zu diesen Eigenschaften finden Sie auf der Referenzseite für das ss-Modell.

Wenn sich der Block in einem Modell mit synchroner Zustandssteuerung befindet (siehe den Block State Control (HDL Coder)), müssen Sie ein Array mit zeitdiskreten Modellen angeben.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	sys
Werte:	ss or idss model array name in quotes

Beispiel: set_param(gcb,"sys","sysArrayName")

Initial condition source — Option zum Festlegen der Anfangsbedingung mit einem externen Signal

internal (Standardeinstellung) | external

Seit R2024b

Legen Sie die Quelle der Anfangsbedingung fest.

• internal – Gibt die Anfangsbedingungen der Zustände mit dem Parameter Initial condition an.

• external – Gibt die Anfangsbedingungen der Zustände mit dem Eingangsport IC des Blocks an.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	InitialConditionSource
Werte:	internal (Standardeinstellung) | external

Initial condition — Anfangsbedingungen

0 (Standardeinstellung) | Vektor

Anfangsbedingungen, die mit dem lokalen Modell zu verwenden sind, um die Simulation zu beginnen, angegeben als Vektor mit Länge gleich der Anzahl der Modellzustände.

Abhängigkeiten

Um diesen Parameter zu aktivieren, setzen Sie Initial condition source auf internal.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	InitialCondition
Werte:	"0" (Standardeinstellung) | initial state values in quotes

Beispiel: set_param(gcb,"InitialCondition","[0 0.1]")

Operating Point Offsets — Offset-Angabeformat

Specify Offsets as double arrays (Standardeinstellung) | Specify offsets as struct array | Use offsets in state-space array

Seit R2024a

Geben Sie das Format für die Betriebspunkt-Offsets an.

• Specify Offsets as double arrays – Gibt die Offsets mithilfe der Parameter Input offset, Output offset, State Offset und State derivative/update offset an.

• Specify offsets as struct array – Gibt die Offsets als Struktur-Array mit den Feldern u, y, x und dx an, die Eingangs-, Ausgangs-, Zustands-, und Zustandsableitungs-Offsets festlegen.

• Use offsets in state-space array – Verwenden Sie die in der Eigenschaft Offsets des Zustandsraum-Arrays festgelegten Offsets.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	opSpecOption
Werte:	"Specify Offsets as double arrays" (Standardeinstellung) | "Specify offsets as struct array" | "Use offsets in state-space array"

Beispiel: set_param(gcb,"opSpecOption","Specify offsets as struct array")

Input offset — Eingangs-Offset

0 (Standardeinstellung) | array

Eingangs-Offsets u(t), wobei Sie eine der folgenden Angaben machen können:

• 0 – Verwenden Sie diesen Wert, wenn keine Eingangs-Offsets vorliegen ($\overline{u}\left(p\right)=0 \forall p$).

• Doppelvektor mit einer Länge, die der Anzahl der Eingänge entspricht – wird verwendet, wenn der Eingangs-Offset im gesamten Planungsraum gleich ist.

• Doppel-Array der Größe n_u-mal-1-mal-N₁-mal-...-mal-N_m – wird verwendet, wenn Offsets vorhanden sind und diese im Planungsraum variieren. Hier ist n_u die Anzahl der Eingänge und N₁-mal-...-mal-N_m die Größe des Planungsrasters. Wenn Ihr Modell beispielsweise über drei Eingänge, zwei Ausgänge und vier Zustände verfügt und über ein 5-mal-6-Raster an Betriebspunkten geplant ist, muss die Größe des Eingangsarrays 3-mal-1-mal-5-mal-6 betragen. Verwenden Sie size(sys), um die Größe des Zustandsraum-Arrays sys zu ermitteln.

Abhängigkeiten

Um diesen Parameter zu aktivieren, setzen Sie das Format Operating Point Offsets auf Specify Offsets as double arrays.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	uOffset
Werte:	"0" (Standardeinstellung) | array name in quotes

Beispiel: set_param(gcb,"uOffset","uOffArray")

Output offset — Ausgangs-Offset

0 (Standardeinstellung) | array

Ausgangs-Offsets y(t), wobei Sie eine der folgenden Angaben machen können:

• 0 – Verwenden Sie diesen Wert, wenn keine Ausgangs-Offsets vorliegen $\overline{y}\left(p\right)=0 \forall p$.

• Double-Vektor mit einer Länge, die der Anzahl der Ausgänge entspricht – wird verwendet, wenn der Ausgangs-Offset im gesamten Planungsraum gleich ist.

• Doppel-Array der Größe n_y-mal-1-mal-N₁-mal-...-mal-N_m – wird verwendet, wenn Offsets vorhanden sind und diese im Planungsraum variieren. Hier ist n_y die Anzahl der Ausgänge und N₁-mal-...-mal-N_m die Größe des Planungsrasters. Wenn Ihr Modell beispielsweise über drei Eingänge, zwei Ausgänge und vier Zustände verfügt und über ein 5-mal-6-Raster an Betriebspunkten geplant ist, muss die Größe des Eingangsarrays 2-mal-1-mal-5-mal-6 betragen. Verwenden Sie size(sys), um die Größe des Zustandsraum-Arrays sys zu ermitteln.

Abhängigkeiten

Um diesen Parameter zu aktivieren, setzen Sie das Format Operating Point Offsets auf Specify Offsets as double arrays.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	yOffset
Werte:	"0" (Standardeinstellung) | array name in quotes

Beispiel: set_param(gcb,"yOffset","yOffArray")

State offset — Zustands-Offset

0 (Standardeinstellung) | array

Zustands-Offsets x(t), wobei Sie eine der folgenden Angaben machen können:

• 0 – Verwenden Sie diesen Wert, wenn keine Zustands-Offsets vorliegen $\overline{x}\left(p\right)=0 \forall p$.

• Double-Vektor mit einer Länge, die der Anzahl der Zustände entspricht – wird verwendet, wenn der Zustands-Offset im gesamten Planungsraum gleich ist.

• Doppel-Array der Größe n_x-mal-1-mal-N₁-mal-...-mal-N_m – wird verwendet, wenn Offsets vorhanden sind und diese im Planungsraum variieren. Hier ist n_x die Anzahl der Zustände und N₁-mal-...-mal-N_m die Größe des Planungsrasters. Wenn Ihr Modell beispielsweise über drei Eingänge, zwei Ausgänge und vier Zustände verfügt und über ein 5-mal-6-Raster an Betriebspunkten geplant ist, muss die Größe des Eingangsarrays 4-mal-1-mal-5-mal-6 betragen. Verwenden Sie size(sys), um die Größe des Zustandsraum-Arrays sys zu ermitteln.

Abhängigkeiten

Um diesen Parameter zu aktivieren, setzen Sie das Format Operating Point Offsets auf Specify Offsets as double arrays.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	xOffset
Werte:	"0" (Standardeinstellung) | array name in quotes

Beispiel: set_param(gcb,"xOffset","xOffArray")

State derivative/update offset — Zustandsableitungs- oder Aktualisierungs-Offset

array

Offsets der Zustandsableitung oder Aktualisierungsvariablen dx(t), wobei Sie eine der folgenden Angaben machen können:

• Wenn Sie das lineare Systemarray durch Linearisierung unter Gleichgewichtsbedingungen erhalten haben, wählen Sie die Option Assume equilibrium operating conditions. Diese Option entspricht einem Offset von $\overline{dx}\left(p\right)=0$ für ein zeitkontinuierliches System und $\overline{dx}\left(p\right)=\overline{x}\left(p\right)$ für ein zeitdiskretes System. Diese Option ist standardmäßig ausgewählt.

• Falls das lineare System mindestens ein System enthält, das Sie unter Nicht-Gleichgewichtsbedingungen erhalten haben, deaktivieren Sie die Option Assume equilibrium operating conditions. Geben Sie eine der folgenden Optionen im Offset value-Feld an:

  • Double-Vektor mit einer Länge, die der Anzahl der Zustände entspricht – wird verwendet, wenn der Zustandsableitungs-Offset im gesamten Planungsraum gleich ist.

  • Doppel-Array der Größe n_x-mal-1-mal-N₁-mal-...-mal-N_m – wird verwendet, wenn Offsets vorhanden sind und diese im Planungsraum variieren. Hier ist n_x die Anzahl der Zustände und N₁-mal-...-mal-N_m die Größe des Planungsrasters. Wenn Ihr Modell beispielsweise über drei Eingänge, zwei Ausgänge und vier Zustände verfügt und über ein 5-mal-6-Raster an Betriebspunkten geplant ist, muss die Größe des Eingangsarrays 4-mal-1-mal-5-mal-6 betragen. Verwenden Sie size(sys), um die Größe des Zustandsraum-Arrays sys zu ermitteln.

Abhängigkeiten

Um diesen Parameter zu aktivieren, setzen Sie das Format Operating Point Offsets auf Specify Offsets as double arrays und deaktivieren Sie Assume equilibrium operating conditions.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	dxOffset
Werte:	"0" (Standardeinstellung) | array name in quotes

Beispiel: set_param(gcb,"dxOffset","dxOffArray")

Struct array — Offsets-Struktur-Array

struct (Standardeinstellung) | Name des Struktur-Arrays

Seit R2024a

Modell-Offsets, angegeben als Struktur mit den folgenden Feldern.

Feld	Beschreibung
u	Eingangs-Offsets
y	Ausgangs-Offsets
x	Zustands-Offsets
dx	Zustandsableitungs-Offsets

• Falls die Offsetwerte im gesamten Planungsraum gleich sind, geben Sie dies als Double-Vektor mit einer Länge an, die der Anzahl der Eingänge, Ausgänge oder Zustände der entsprechenden Felder entspricht.

• Wenn die Offsets über den Planungsraum hinweg schwanken, legen Sie ein Struktur-Array fest. Nehmen wir beispielsweise an, dass Ihr Modell über drei Eingänge, zwei Ausgänge und vier Zustände verfügt. Wenn Sie Ihr Modell mit einem 5-mal-6-Array aus Betriebspunkten linearisieren, muss die Größe des Struktur-Arrays 5-mal-6 sein und jeder Eintrag muss einen Vektor mit Länge gleich der Anzahl Eingänge, Ausgänge oder Zustände der entsprechenden Felder enthalten.

Die Funktion linearize (Simulink Control Design) gibt die Offsets in diesem Format über den Ausgang info.Offsets aus, wenn Sie eine Linearisierung mit auf true gesetzter Funktion StoreOffsets durchführen.

Abhängigkeiten

Um diesen Parameter zu aktivieren, setzen Sie das Format Operating Point Offsets auf Specify Offsets as struct array. (seit R2024a)

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	Offset
Werte:	"struct" (Standardeinstellung) | structure array name in quotes

Beispiel: set_param(gcb,"Offset","OffsetStructName")

Registerkarte feste Einträge

In bestimmten Fällen kann Ihr LPV-Modell Koeffizienten mit kleinen Variationen umfassen. Über die Parameter dieser Registerkarte können Sie festlegen, welche Modellmatrizen fest sind und deren Nennwerte festlegen, um Einträge in den Modelldaten zu übersteuern. In manchen Situationen empfiehlt es sich, für die Simulation eine parameterabhängige Matrix wie A(p) durch einen festen Wert A* zu ersetzen. Zum Beispiel kann A* einen Durchschnittswert über den Planungsbereich darstellen. Standardmäßig verwendet der Block die Daten des State-space array, um zu entscheiden, welche Einträge fest oder variabel sind (aus Leistungsgründen interpoliert der Block variable Einträge).

Auf dieser Registerkarte können Sie dieses Standardverhalten überschreiben, um beispielsweise das LPV-Modell zu vereinfachen. Sie können beispielsweise entscheiden, dass der dritte Eintrag von A nicht stark variabel ist und Sie ihn auf einen festen Durchschnittswert setzen möchten. Die logischen Arrays geben an, welche Einträge als fest behandelt werden sollten, und Read values from gibt an, welcher Wert für diese festen Einträge verwendet werden soll. false übersteuert die LTI-Arraydaten nicht; hierbei wird die Entscheidung, ob ein Eintrag fest oder variabel ist, anhand der Daten getroffen.

Coefficients To Fix — Feste Koeffizienten von Zustandsraum-Matrizen

false oder 0 (Standardeinstellung) | true oder 1 | logische Matrix

Geben Sie die Positionen dieser Koeffizienten mit einer der folgenden Optionen an:

• Skalarer boolescher Wert (true oder false), falls alle Einträge einer Matrix gleich behandelt werden sollen.

  Der Standardwert für die Zustandsraum-Matrizen und Verzögerungsvektoren ist false, sie werden also als frei behandelt.

• Logische Matrix mit einer Größe, die mit der Größe der entsprechenden Matrix kompatibel ist:

  Zustandsraum-Matrix	Größe der Matrix mit festen Einträgen
  A matrix	nx-mal-nx
  B matrix	nx-mal-nu
  C matrix	ny-mal-nx
  D matrix	ny-mal-nu
  Input delay	nu-mal-1
  Output delay	ny-mal-1
  Internal delay	ni-mal-1

  hierbei ist n_u die Anzahl der Eingänge, n_y die Anzahl der Ausgänge, n_x die Anzahl der Zustände und n_i die Länge des internen Verzögerungsvektors.

• Numerische Indizes zur Angabe der Position der festen Einträge. Weitere Informationen darüber, wie Sie numerische Indizes erzeugen, die einem bestimmten Index (i,j) für ein Element einer Matrix entsprechen, finden Sie auf der sub2ind-Referenzseite.

Haben Sie die Position angegeben, stellen Sie die Werte des festen Koeffizienten mithilfe des Parameters Read values from bereit.

Read values from — Quelle für die Werte fester Koeffizienten

First model in state-space array (Standardeinstellung) | Custom state-space model

Zustandsraummodell, das die Werte der festen Koeffizienten liefert und wie folgt spezifiziert werden kann:

• First model in state-space array – Das erste Modell im Zustandsraum-Array wird für die festen Koeffizienten des LPV-Modells verwendet. Im folgenden Beispiel wird das Zustandsraum-Array durch das Objekt sys angegeben und die festen Koeffizienten werden dem Modell sys(:,:,1) entnommen.

  % Specify a 4-by-5 array of state-space models.
  sys = rss(4,2,3,4,5);
  a = 1:4; 
  b = 10:10:50;
  [av,bv] = ndgrid(a,b);
  % Use "alpha" and "beta" variables as scheduling parameters.
  sys.SamplingGrid = struct('alpha',av,'beta',bv);  

  Die festen Koeffizienten werden dem Modell sysFixed = sys(:,:,1) entnommen, das [alpha=1, beta=10] entspricht. Falls der (2,1)-Eintrag der A-Matrix zwangsweise fest ist, wird während der Simulation sysFixed.A(2,1) als sein Wert verwendet.

• Custom state-space model: Geben Sie für feste Einträge ein anderes Zustandsraummodell an. Legen Sie im Custom model-Feld eine Variable für das feste Modell an. Das feste Modell muss die gleiche Zustandsgrundlage verwenden wie das Zustandsraum-Array im LPV-Modell.

Registerkarte Planung

Interpolation method — Interpolationsmethode

Linear (Standardeinstellung) | Nearest | Flat

Die Interpolationsmethode. Sie legt fest, wie die Zustandsraumdaten für Planungsparameter-Werte berechnet werden müssen, die sich außerhalb ihrer Gitterposition befinden.

Geben Sie eine der folgenden Optionen an:

• Flat: Wählen Sie die Zustandsraumdaten an jenem Gitterpunkt, der dem aktuellen Punkt am nächsten liegt, aber nicht größer ist als dieser Punkt. Der aktuelle Punkt ist der Wert der Planungsparameter zum aktuellen Zeitpunkt.

• Nearest: Wählen Sie die Zustandsraumdaten am nächstgelegenen Gitterpunkt im Planungsraum.

• Linear: Erhalten Sie Zustandsraumdaten durch lineare Interpolation der nächsten 2d-Nachbarn im Planungsraum, wobei gilt: d = Anzahl der Planungsparameter.

Das Standardinterpolationsschema für regelmäßige Gitter von Planungsparameterwerten ist Linear. Für unregelmäßige Raster wird unabhängig von der getroffenen Wahl immer das Interpolationsschema Nearest verwendet. Weitere Informationen über regelmäßige und unregelmäßige Gitter finden Sie unter Regular vs. Irregular Grids.

Die Methode Linear bietet die höchste Genauigkeit, die Berechnung dauert aber länger. Die Methoden Flat und Nearest eignen sich gut für Modelle, die über Moduswechsel-Dynamik verfügen.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	IMethod
Werte:	"Linear" (Standardeinstellung) | "Nearest" | "Flat"

Beispiel: set_param(gcb,"IMethod","Flat")

Extrapolation method — Extrapolationsmethode

Clip (Standardeinstellung) | Linear

Die Extrapolationsmethode. Sie legt fest, wie die Zustandsraumdaten für Planungsparameter-Werte berechnet werden müssen, die sich außerhalb des Bereiches befinden, für den das Zustandsraum-Array bereitgestellt wurde (wie in der Eigenschaft SamplingGrid festgelegt).

Geben Sie eine der folgenden Optionen an:

• Clip (Standardeinstellung) – deaktiviert die Extrapolation und liefert die Daten, die dem letzten verfügbaren Planungsrasterpunkt entsprechen, der dem aktuellen Punkt am nächsten liegt.

• Linear – erstellt eine Linie zwischen dem ersten oder letzten Wertepaar für jeden Planungsparameter an, je nachdem, ob der aktuelle Wert kleiner als der erste oder größer als der letzte Gitterpunktwert ist. Diese Methode liefert den Punkt auf dieser Linie, der dem aktuellen Wert entspricht. Bei der linearen Extrapolation muss auch das Interpolationsschema linear sein.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	EMethod
Werte:	"Clip" (Standardeinstellung) | "Linear"

Beispiel: set_param(gcb,"EMethod","Linear")

Index search method — Prelookup-Algorithmus

Binary search (Standardeinstellung) | Linear search

Der Block ermittelt die Position der aktuellen Planungsparameter-Werte im Planungsraum mithilfe eines Prelookup-Algorithmus. Wählen Sie Linear search oder Binary search. Jede Suchmethode bietet in verschiedenen Situationen Geschwindigkeitsvorteile. Weitere Informationen zu diesem Parameter finden Sie auf der Prelookup (Simulink)-Referenzseite.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Um den Blockparameter-Wert programmatisch abzurufen, verwenden Sie die Funktion get_param (Simulink).

Parameter:	IndexSearch
Werte:	"Binary Search" (Standardeinstellung) | "Linear Search"

Beispiel: set_param(gcb,"IndexSearch","Linear Search")

Begin index search using previous index result — Suche im vorherigen Zeitschritt beginnen

on (Standardeinstellung) | off

Aktivieren Sie dieses Kontrollkästchen, wenn Sie möchten, dass der Block seine Suche mit dem Index aus dem vorangegangenen Zeitschritt beginnt. Weitere Informationen zu diesem Parameter finden Sie auf der Prelookup (Simulink)-Referenzseite.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	IndexBegin
Werte:	"on" (Standardeinstellung) | "off"

Beispiel: set_param(gcb,"IndexBegin","off")

Registerkarte Codegenerierung

Block data type (discrete-time case only) — Block-Datentyp

double (Standardeinstellung) | single

Block-Datentyp, angegeben als double oder single.

Abhängigkeiten

Um diese Option zu aktivieren, verwenden Sie ein diskretes Zustandsraummodell als Eingang.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	DataType
Werte:	"double" (Standardeinstellung) | "single"

Beispiel: set_param(gcb,"DataType","single")

Initial buffer size for delays — Anfängliche Puffergröße

1024 (Standardeinstellung) | Positive ganze Zahl über 5

Anfängliche Speicherzuweisung für die Anzahl der Eingangspunkte, die für Modelle, die Verzögerungen enthalten, gespeichert werden sollen. Wenn die Anzahl der Eingangspunkte die anfängliche Puffergröße überschreitet, weist der Block zusätzlichen Speicher zu. Die Standardgröße ist 1024.

Wenn Sie das Modell im Accelerator-Modus ausführen oder das Modell erstellen, versichern Sie sich, dass die anfängliche Puffergröße groß genug ist, um die maximale erwartete Verzögerung im Modell zu bewältigen.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	InitBufferSize
Werte:	"1024" (Standardeinstellung) | positive integer greater than 5 in quotes

Beispiel: set_param(gcb,"InitBufferSize","512")

Use fixed buffer size — Verwenden einer festen Puffergröße

off (Standardeinstellung) | on

Geben Sie an, ob eine feste Puffergröße verwendet werden soll, um verzögerte Eingangs- und Ausgangsdaten aus früheren Zeitschritten zu speichern. Verwenden Sie diese Option für zeitkontinuierliche LPV-Systeme, die Eingangs- oder Ausgangsverzögerungen enthalten. Wenn der Puffer voll ist, ersetzen neue Daten die bereits im Puffer befindlichen Daten. Die Software verwendet die lineare Extrapolation, um Ausgabewerte zu schätzen, die sich nicht im Puffer befinden.

Programmgesteuerte Verwendung

Um den Blockparameter-Wert programmatisch festzulegen, verwenden Sie die Funktion set_param (Simulink).

Parameter:	FixedBuffer
Werte:	"off" (Standardeinstellung) | "on"

Beispiel: set_param(gcb,"FixedBuffer","on")

Erweiterte Fähigkeiten

C/C++ Codegenerierung
Generieren von C und C++ Code mit Simulink® Coder™.

Versionsverlauf

Eingeführt in R2014b

R2024b: Externes Angeben der Anfangsbedingungen als Block-Eingang

Mit dem LPV System-Block können Sie die Anfangszustand-Werte bei dem Block-Eingangsport IC festlegen. Um diesen Port zu aktivieren, setzen Sie den Parameter Initial condition source auf external.

R2024b: Der Anfangszustand-Parameter x0 wurde zu InitialCondition umbenannt

Der Anfangszustand-Parameter x0 wird nun als InitialCondition bezeichnet. Wenn Ihr Code diesen Parameter programmatisch festlegt, beispielsweise über set_param(blockPath,"x0","[0 0.1]"), aktualisieren Sie Ihren Code auf set_param(blockPath,"InitialCondition","[0 0.1]").

R2024a: Verbesserte Unterstützung für Offset und weitere Verbesserungen

Der LPV System-Block unterstützt nun eine Angabe von Betriebspunkt-Offsets in zwei neuen Formaten:

• Angabe von Offsets als Struct-Array

• Verwendung von Offsets in einem Zustandsraum-Array

Vor Version R2024a unterstützte der Block eine Angabe von Offsets nur als Double-Arrays in den Blockparametern. Verwenden Sie die Liste Operating Point Offsets (Betriebspunkt-Offsets), um das Format der Offsets festzulegen.

Zudem wurden die folgenden Verbesserungen am Block vorgenommen:

• Die Block-Architektur verwendet nun einen zugrundeliegenden Varying State Space-Block. Dies vereinfacht die Unterstützung von Offsets.

• Dieser Block unterstützt nun einen schnellen Neustart für die Simulation. In diesem Modus können nur die Block-Eingänge und der Parameter Initial state optimiert werden. Die übrigen Blockparameter können nicht optimiert werden, da eine Änderung hier die Modelltopologie verändert.

R2024a: Ignoriert konstante Parameter in SamplingGrid

Der LPV System-Block ignoriert nun die Singleton-Dimension und konstante Parameter im Abtastraster des Eingangsmodell-Arrays. Daher dürfen Sie die Parameter, also die Felder der Struktur SamplingGrid mit konstanten Werten, nicht dem par-Port des Blocks übergeben. Verwenden Sie für diesen Port nur die variablen Felder.

Vor Version R2024a gab der Block einen Fehler aus, wenn Parameter mit konstanten Werten übergeben wurden.

Siehe auch

Themen

• LTV and LPV Modeling
• Using LTV and LPV Models in MATLAB and Simulink