getIOTransfer
Transfer function for specified I/O set using slLinearizer or slTuner interface
Syntax
Description
linsys = getIOTransfer(s,in,out)slLinearizer or slTuner interface,
s.
The software enforces all the permanent openings
specified for s when it calculates
linsys. For information on how
getIOTransfer treats in and
out, see Transfer Functions. If you configured either
s.Parameters, or s.OperatingPoints, or
both, getIOTransfer performs multiple linearizations and
returns an array of transfer functions.
linsys = getIOTransfer(s,ios)ios for the model associated with
s. Use the linio command to create
ios. The software enforces the linearization I/O type
of each signal specified in ios when it calculates
linsys. The software also enforces all the permanent
loop openings specified for s.
linsys = getIOTransfer(___,mdl_index)mdl_index specifies the index of the linearizations of
interest, in addition to any of the input arguments in previous syntaxes.
Use this syntax for efficient linearization, when you want to obtain the transfer function for only a subset of the batch linearization results.
Examples
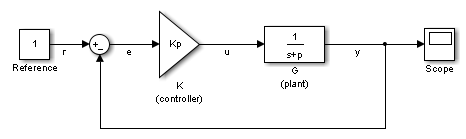
Obtain the closed-loop transfer function from the reference signal, r, to the plant output, y, for the ex_scd_simple_fdbk model.
Open the ex_scd_simple_fdbk model.
mdl = 'ex_scd_simple_fdbk';
open_system(mdl);
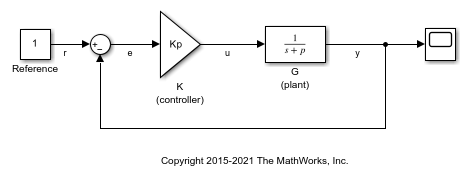
In this model:

Create an slLinearizer interface for the model.
sllin = slLinearizer(mdl);
To obtain the closed-loop transfer function from the reference signal, r, to the plant output, y, add both points to sllin.
addPoint(sllin,{'r','y'});
Obtain the closed-loop transfer function from r to y.
sys = getIOTransfer(sllin,'r','y'); tf(sys)
ans =
From input "r" to output "y":
3
-----
s + 8
Continuous-time transfer function.
The software adds a linearization input at r, dr, and a linearization output at y.
sys is the transfer function from dr to y, which is equal to  .
.
Obtain the plant model transfer function, G, for the ex_scd_simple_fdbk model.
Open the ex_scd_simple_fdbk model.
mdl = 'ex_scd_simple_fdbk';
open_system(mdl);

In this model:
Create an slLinearizer interface for the model.
sllin = slLinearizer(mdl);
To obtain the plant model transfer function, use u as the input point and y as the output point. To eliminate the effects of feedback, you must break the loop. You can break the loop at u, e, or y. For this example, break the loop at u. Add these points to sllin.
addPoint(sllin,{'u','y'});
Obtain the plant model transfer function.
sys = getIOTransfer(sllin,'u','y','u'); tf(sys)
ans =
From input "u" to output "y":
1
-----
s + 5
Continuous-time transfer function.
The second input argument specifies u as the input, while the fourth input argument specifies u as a temporary loop opening.
sys is the transfer function from du to y, which is equal to 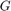 .
.
Suppose you batch linearize the scdcascade model for multiple transfer functions. For most linearizations, you vary the proportional (Kp2) and integral gain (Ki2) of the C2 controller in the 10% range. For this example, calculate the open-loop response transfer function for the inner loop, from e2 to y2, for the maximum value of Kp2 and Ki2.
Open the scdcascade model.
mdl = 'scdcascade';
open_system(mdl)
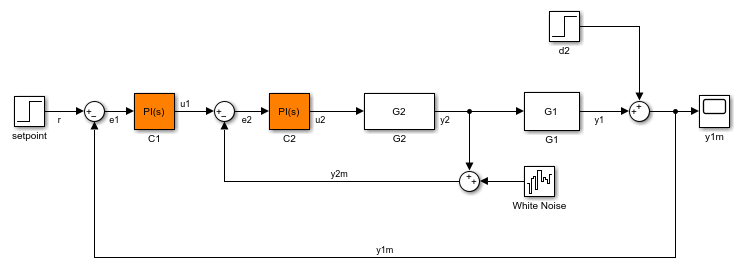
Create an slLinearizer interface for the model.
sllin = slLinearizer(mdl);
Vary the proportional (Kp2) and integral gain (Ki2) of the C2 controller in the 10% range.
Kp2_range = linspace(0.9*Kp2,1.1*Kp2,3); Ki2_range = linspace(0.9*Ki2,1.1*Ki2,5); [Kp2_grid,Ki2_grid] = ndgrid(Kp2_range,Ki2_range); params(1).Name = 'Kp2'; params(1).Value = Kp2_grid; params(2).Name = 'Ki2'; params(2).Value = Ki2_grid; sllin.Parameters = params;
To calculate the open-loop transfer function for the inner loop, use e2 and y2 as analysis points. To eliminate the effects of the outer loop, break the loop at e2. Add e2 and y2 to sllin as analysis points.
addPoint(sllin,{'e2','y2'})
Determine the index for the maximum values of Ki2 and Kp2.
mdl_index = params(1).Value == max(Kp2_range) & params(2).Value == max(Ki2_range);
Obtain the open-loop transfer function from e2 to y2.
sys = getIOTransfer(sllin,'e2','y2','e2',mdl_index);
Open Simulink® model.
mdl = 'scdcascade';
open_system(mdl)

Create a linearization option set, and set the StoreOffsets option.
opt = linearizeOptions('StoreOffsets',true);
Create slLinearizer interface.
sllin = slLinearizer(mdl,opt);
Add analysis points to calculate the closed-loop transfer function.
addPoint(sllin,{'r','y1m'});
Calculate the input/output transfer function, and obtain the corresponding linearization offsets.
[sys,info] = getIOTransfer(sllin,'r','y1m');
View offsets.
info.Offsets
ans =
struct with fields:
dx: [6×1 double]
x: [6×1 double]
u: 1
y: 0
OutputName: {'y1m'}
InputName: {'r'}
StateName: {6×1 cell}
Ts: 0
Input Arguments
Interface to a Simulink model, specified as either an slLinearizer interface or an slTuner interface.
Input analysis point signal name, specified as:
Character vector or string — Analysis point signal name.
To determine the signal name associated with an analysis point, type
s. The software displays the contents ofsin the MATLAB® command window, including the analysis point signal names, block names, and port numbers. Suppose that an analysis point does not have a signal name, but only a block name and port number. You can specifyinas the block name. To use a point not in the list of analysis points fors, first add the point usingaddPoint.You can specify
inas a uniquely matching portion of the full signal name or block name. Suppose that the full signal name of an analysis point is'LoadTorque'. You can specifyinas'Torque'as long as'Torque'is not a portion of the signal name for any other analysis point ofs.For example,
in = 'y1m'.Cell array of character vectors or string array — Specifies multiple analysis point names. For example,
in = {'y1m','y2m'}.
Output analysis point signal name, specified as:
Character vector or string — Analysis point signal name.
To determine the signal name associated with an analysis point, type
s. The software displays the contents ofsin the MATLAB command window, including the analysis point signal names, block names, and port numbers. Suppose that an analysis point does not have a signal name, but only a block name and port number. You can specifyoutas the block name. To use a point not in the list of analysis points fors, first add the point usingaddPoint.You can specify
outas a uniquely matching portion of the full signal name or block name. Suppose that the full signal name of an analysis point is'LoadTorque'. You can specifyoutas'Torque'as long as'Torque'is not a portion of the signal name for any other analysis point ofs.For example,
out = 'y1m'.Cell array of character vectors or string array — Specifies multiple analysis point names. For example,
out = {'y1m','y2m'}.
Temporary opening signal name, specified as:
Character vector or string — Analysis point signal name.
temp_openingmust specify an analysis point that is in the list of analysis points fors. To determine the signal name associated with an analysis point, types. The software displays the contents ofsin the MATLAB command window, including the analysis point signal names, block names, and port numbers. Suppose that an analysis point does not have a signal name, but only a block name and port number. You can specifytemp_openingas the block name. To use a point not in the list of analysis points fors, first add the point usingaddPoint.You can specify
temp_openingas a uniquely matching portion of the full signal name or block name. Suppose that the full signal name of an analysis point is'LoadTorque'. You can specifytemp_openingas'Torque'as long as'Torque'is not a portion of the signal name for any other analysis point ofs.For example,
temp_opening = 'y1m'.Cell array of character vectors or string array — Specifies multiple analysis point names. For example,
temp_opening = {'y1m','y2m'}.
Linearization I/Os, created using linio,
specified as a linearization I/O object.
ios must specify signals that are in the
list of analysis points for s. To view the list
of analysis points, type s. To use a point that
is not in the list of analysis points for s,
you must first add the point to the list using addPoint.
For example:
ios(1) = linio('scdcascade/setpoint',1,'input'); ios(2) = linio('scdcascade/Sum',1,'output');
Here, ios(1) specifies an input, and ios(2) specifies
an output.
Index for linearizations of interest, specified as:
Array of logical values — Logical array index of linearizations of interest. Suppose that you vary two parameters,
par1andpar2, and want to extract the linearization for the combination ofpar1 > 0.5andpar2 <= 5. Use:params = s.Parameters; mdl_index = params(1).Value>0.5 & params(2).Value <= 5;
The expression
params(1).Value>0.5 & params(2).Value<5uses logical indexing and returns a logical array. This logical array is the same size asparams(1).Valueandparams(2).Value. Each entry contains the logical evaluation of the expression for corresponding entries inparams(1).Valueandparams(2).Value.Vector of positive integers — Linear index of linearizations of interest. Suppose that you vary two parameters,
par1andpar2, and want to extract the linearization for the combination ofpar1 > 0.5andpar2 <= 5. Use:params = s.Parameters; mdl_index = find(params(1).Value>0.5 & params(2).Value <= 5);
The expression
params(1).Value>0.5 & params(2).Value<5returns a logical array.findreturns the linear index of every true entry in the logical array
Output Arguments
Transfer function for specified I/Os, returned as described in the following:
If you did not configure
s.Parametersands.OperatingPoints, the software calculateslinsysusing the default model parameter values. The software uses the model initial conditions as the linearization operating point.linsysis returned as a state-space model.If you configured
s.Parametersonly, the software computes a linearization for each parameter grid point.linsysis returned as a state-space model array of the same size as the parameter grid.If you configured
s.OperatingPointsonly, the software computes a linearization for each specified operating point.linsysis returned as a state-space model array of the same size ass.OperatingPoints.If you configured
s.Parametersand specifieds.OperatingPointsas a single operating point, the software computes a linearization for each parameter grid point. The software uses the specified operating point as the linearization operating point.linsysis returned as a state-space model array of the same size as the parameter grid.If you configured
s.Parametersand specifieds.OperatingPointsas multiple operating point objects, the software computes a linearization for each parameter grid point. The software requires thats.OperatingPointsis the same size as the parameter grid specified bys.Parameters. The software computes each linearization using corresponding operating points and parameter grid points.linsysis returned as a state-space model array of the same size as the parameter grid.If you configured
s.Parametersand specifieds.OperatingPointsas multiple simulation snapshot times, the software simulates and linearizes the model for each snapshot time and parameter grid point combination. Suppose that you specify a parameter grid of sizepandNsnapshot times.linsysis returned as a state-space model array of sizeN-by-p.
For most models, linsys is returned as an ss object or an array of
ss objects. However, if your model contains one of
the following blocks in the linearization path defined by
in and out, then
linsys returns the specified type of state-space
model.
| Block | linsys Type |
|---|---|
Block with a substitution specified as a
genss object or tunable model
object | genss |
Block with a substitution specified as an uncertain
model, such as uss | uss (Robust Control Toolbox) |
| Sparse Second Order block | mechss |
| Descriptor State-Space block configured to linearize to a sparse model | sparss |
Linearization information, returned as a structure with the following fields:
Linearization offsets, returned as [] if
s.Options.StoreOffsets is false.
Otherwise, Offsets is returned as one of the
following:
If
linsysis a single state-space model, thenOffsetsis a structure.If
linsysis an array of state-space models, thenOffsetsis a structure array with the same dimensions aslinsys.
Each offset structure has the following fields:
| Field | Description |
|---|---|
x | State offsets used for linearization, returned as a column vector of length
nx, where
nx is the number of states in
linsys. |
y | Output offsets used for linearization, returned as a column vector of length
ny, where
ny is the number of outputs in
linsys. |
u | Input offsets used for linearization, returned as a column vector of length
nu, where
nu is the number of inputs in
linsys. |
dx | Derivative offsets for continuous time systems or updated state values for discrete-time systems, returned as a column vector of length nx. |
StateName | State names, returned as a cell array that contains
nx elements that match the names
in linsys.StateName. |
InputName | Input names, returned as a cell array that contains
nu elements that match the names
in linsys.InputName. |
OutputName | Output names, returned as a cell array that contains
ny elements that match the names
in linsys.OutputName. |
Ts | Sample time of the linearized system, returned as a scalar that matches the sample time in
linsys.Ts. For continuous-time systems,
Ts is 0. |
If Offsets is a structure array, you can
configure an LPV System block using
the offsets. To do so, first convert them to the required format using getOffsetsForLPV. For an example, see Approximate Nonlinear Behavior Using Array of LTI Systems.
Linearization diagnostic information, returned as [] if
s.Options.StoreAdvisor is false.
Otherwise, Advisor is returned as one of the
following:
If
linsysis a single state-space model,Advisoris aLinearizationAdvisorobject.If
linsysis an array of state-space models,Advisoris an array ofLinearizationAdvisorobjects with the same dimensions aslinsys.
LinearizationAdvisor objects store linearization
diagnostic information for individual linearized blocks. For an example of
troubleshooting linearization results using a
LinearizationAdvisor object, see Troubleshoot Linearization Results at Command Line.
More About
A transfer function is an LTI system response at a linearization output point to a linearization input. You perform linear analysis on transfer functions to understand the stability, time-domain characteristics, or frequency-domain characteristics of a system.
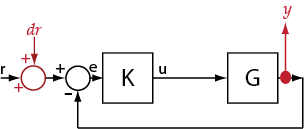
You can calculate multiple transfer functions for a given block
diagram. Consider the ex_scd_simple_fdbk model:
You can calculate the transfer function from the reference input
signal to the plant output signal. The reference input (also
referred to as setpoint), r,
originates at the Reference block, and the plant
output, y, originates at the G block.
This transfer function is also called the overall closed-loop transfer
function. To calculate this transfer function, the software adds a
linearization input at r, dr,
and a linearization output at y.
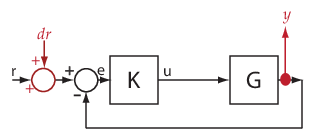
The software calculates the overall closed-loop transfer function
as the transfer function from dr to y,
which is equal to (I+GK)-1GK.
Observe that the transfer function from r to y is
equal to the transfer function from dr to y.
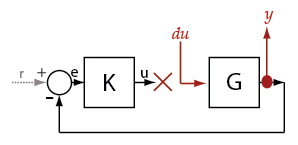
You can calculate the plant transfer function from
the plant input, u, to the plant output, y.
To isolate the plant dynamics from the effects of the feedback loop,
introduce a loop break (or opening) at y, e,
or, as shown, at u.

The software breaks the loop and adds a linearization input, du,
at u, and a linearization output at y.
The plant transfer function is equal to the transfer function from du to y,
which is G.
Similarly, to obtain the controller transfer function,
calculate the transfer function from the controller input, e,
to the controller output, u. Break the feedback
loop at y, e, or u.
You can use getIOTransfer to obtain various
open-loop and closed-loop transfer functions. To configure the transfer
function, specify analysis
points as inputs, outputs, and openings (temporary or permanent), in
any combination. The software treats each combination uniquely. Consider
the following code that shows some different ways that you can use
the analysis point, u, to obtain a transfer function:
sllin = slLinearizer('ex_scd_simple_fdbk') addPoint(sllin,{'u','e','y'}) T0 = getIOTransfer(sllin,'e','y','u'); T1 = getIOTransfer(sllin,'u','y'); T2 = getIOTransfer(sllin,'u','y','u'); T3 = getIOTransfer(sllin,'y','u'); T4 = getIOTransfer(sllin,'y','u','u'); T5 = getIOTransfer(sllin,'u','u'); T6 = getIOTransfer(sllin,'u','u','u');
In T0, u specifies a loop
break. In T1, u specifies only
an input, whereas in T2, u specifies
an input and an opening, also referred to as an open-loop
input. In T3, u specifies
only an output, whereas in T4, u specifies
an output and an opening, also referred to as an open-loop
output. In T5, u specifies
an input and an output, also referred to as a complementary
sensitivity point. In T6, u specifies
an input, an output, and an opening, also referred to as a loop
transfer point. The table describes how getIOTransfer treats
the analysis points, with an emphasis on the different uses of u.
u Specifies... | How getIOTransfer Treats
Analysis Points | Transfer Function |
|---|---|---|
Loop break Example code: T0 = getIOTransfer(...
sllin,'e','y','u') |
The software stops the signal flow at
|
|
Input Example code: T1 = getIOTransfer(...
sllin,'u','y') |
The software adds a linearization input,
|
|
Open-loop input Example code: T2 = getIOTransfer(...
sllin,'u','y','u') |
The software breaks the signal flow and adds
a linearization input, |
|
Output Example code: T3 = getIOTransfer(...
sllin,'y','u') |
The software adds a linearization input,
|
|
Open-loop output Example code: T4 = getIOTransfer(...
sllin,'y','u','u') |
The software adds a linearization input,
|
|
Complementary sensitivity point Example code: T5 = getIOTransfer(...
sllin,'u','u')Tip You also can obtain the complementary sensitivity function
using |
The software adds a linearization output and
a linearization input, |
|
Loop transfer function point Example code: T6 = getIOTransfer(...
sllin,'u','u','u')Tip You also can obtain the loop transfer function using
|
The software adds a linearization output,
breaks the loop, and adds a linearization input,
|
|
The software does not modify the Simulink model when it computes the transfer function.
Analysis points, used
by the slLinearizer and slTuner interfaces,
identify locations within a model that are relevant for linear analysis
and control system tuning. You use analysis points as inputs to the
linearization commands, such as getIOTransfer, getLoopTransfer, getSensitivity, and getCompSensitivity. As inputs to the
linearization commands, analysis points can specify any open-loop
or closed-loop transfer function in a model. You can also use analysis
points to specify design requirements when tuning control systems
using commands such as systune.
Location refers to a specific block output port within a model or to a bus element in such an output port. For convenience, you can use the name of the signal that originates from this port to refer to an analysis point.
You can add analysis points to an slLinearizer or slTuner interface, s,
when you create the interface. For example:
s = slLinearizer('scdcascade',{'u1','y1'});
Alternatively, you can use the addPoint command.
To view all the analysis points of s, type s at
the command prompt to display the interface contents. For each analysis
point of s, the display includes the block name
and port number and the name of the signal that originates at this
point. You can also programmatically obtain a list of all the analysis
points using getPoints.
For more information about how you can use analysis points, see Mark Signals of Interest for Control System Analysis and Design and Mark Signals of Interest for Batch Linearization.
Permanent openings,
used by the slLinearizer and slTuner interfaces,
identify locations within a model where the software breaks the signal
flow. The software enforces these openings for linearization and tuning.
Use permanent openings to isolate a specific model component. Suppose
that you have a large-scale model capturing aircraft dynamics and
you want to perform linear analysis on the airframe only. You can
use permanent openings to exclude all other components of the model.
Another example is when you have cascaded loops within your model
and you want to analyze a specific loop.
Location refers to a specific block output port within a model. For convenience, you can use the name of the signal that originates from this port to refer to an opening.
You can add permanent openings to an slLinearizer or slTuner interface, s,
when you create the interface or by using the addOpening command. To remove a location
from the list of permanent openings, use the removeOpening command.
To view all the openings of s, type s at
the command prompt to display the interface contents. For each permanent
opening of s, the display includes the block name
and port number and the name of the signal that originates at this
location. You can also programmatically obtain a list of all the permanent
loop openings using getOpenings.
Version History
Introduced in R2013bYou can linearize and obtain a sparse model from a Simulink model that contains a Sparse Second Order or Descriptor State-Space block.
mechssmodel when you use a Sparse Second Order in your Simulink model.sparssmodel when you use a Descriptor State-Space block and select the Linearize to sparse model block parameter.
For more information, see Sparse Model Basics. For an example, see Linearize Simulink Model to a Sparse Second-Order Model Object.
You can compute operating point offsets for model inputs, outputs, states, and state derivatives when linearizing Simulink models. Thee offsets streamline the creation of linear parameter-varying (LPV) systems.
To obtain operating point offsets, first create a linearizeOptions or slTunerOptions object and set the
StoreOffsets option to true. Then,
create an slLinearizer or slTuner interface for the
model.
You can extract the offsets from the info output argument of
getIOTransfer and convert them into the required format for
the LPV System block using the getOffsetsForLPV function.
See Also
slLinearizer | slTuner | addPoint | addOpening | getLoopTransfer | getSensitivity | getCompSensitivity
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)





