Neural Network for Digital Predistortion DesignOffline Training
This example shows how to design, train, and test a neural network to apply digital predistortion (DPD) to offset the effects of nonlinearities in a power amplifier (PA). The example focuses on offline training of the neural network-based DPD (NN-DPD). In this example, you:
Design and train a fully connected neural network as a DPD.
Test the NN-DPD using a real PA.
Compare the results to that of cross-term memory polynomial DPD.
Introduction
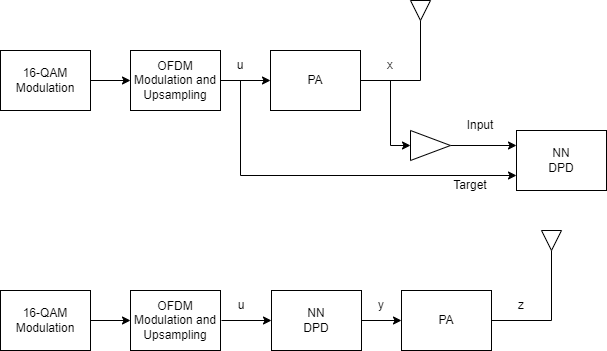
This diagram shows the offline training workflow. First, you train an NN-DPD by using the input and output signals of the PA. Then, you use the trained NN-DPD.
The upper path shows the neural network training workflow. During training, you measure the input to the PA, , and the output of the PA, . To train the neural network as the inverse of the PA and use it for DPD, use as the input signal and as the target signal. This process uses indirect learning [1].
The lower path shows the deployed workflow with the trained NN-DPD inserted before the PA. In this configuration, the NN-DPD inputs the oversampled signal, , and output, , as the input to the PA. The PA output is the linearized signal.
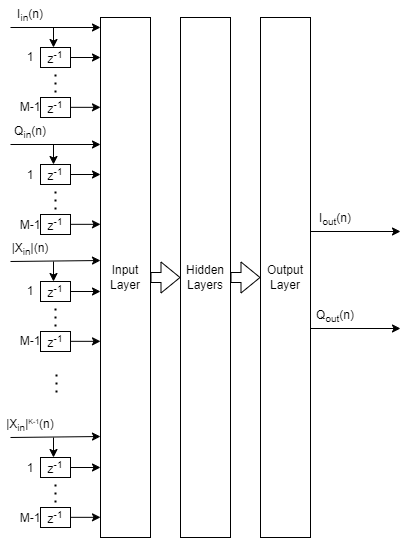
NN-DPD Structure
Design an augmented real-valued time-delay neural network (ARVTDNN) as described in [2]. ARVTDNN has multiple fully connected layers and an augmented input.
The memory polynomial model has been commonly applied in the behavioral modeling and predistortion of PAs with memory effects. This equation shows the PA memory polynomial.
The output is a function of the delayed versions of the input signal, , and also powers of the amplitudes of and its delayed versions.
Theoretically, a neural network can approximate any function provided that it has enough layers and neurons per layer. You can input to the neural network and approximate , or its inverse, which is the DPD function. To decrease the required complexity of the neural network in terms of number of layers and neurons, apply the expert knowledge provided by the memory polynomial approximation and provide the neural network extra features in the form of and .
The NN-DPD has multiple fully connected layers. The input layer inputs the in-phase and quadrature components (/) of the complex baseband samples. The / samples and delayed versions are used as part of the input to account for the memory in the PA model. Also, the amplitudes of the / samples up to the power are fed as input to account for the nonlinearity of the PA.
During training,
while during deployment (inference),
where and are the real and imaginary part operators, respectively.
Prepare Data
Generate training, validation, and testing data. Use the training and validation data to train the NN-DPD. Use the test data to evaluate the NN-DPD performance. For details, see the Data Preparation for Neural Network Digital Predistortion Design example.
Choose Data Source and Bandwidth
Choose the data source for the system. This example uses an NXP™ Airfast LDMOS Doherty PA, which is connected to a local NI™ VST, as described in the Power Amplifier Characterization example. If you do not have access to a PA, run the example with simulated PA or saved data. Simulated PA uses a neural network PA model, which is trained using data captured from the PA using an NI VST. If you choose saved data, the example downloads data files.
dataSource ="Simulated PA"; if strcmp(dataSource,"Saved data") helperNNDPDDownloadData("dataprep") end
Generate Training Data
Generate oversampled OFDM signals.
[txWaveTrain,txWaveVal,txWaveTest,qamRefSymTrain,qamRefSymVal, ...
qamRefSymTest,ofdmParams] = generateOversampledOFDMSignals;
Fs = ofdmParams.SampleRate;
bw = ofdmParams.Bandwidth;Pass signals through the PA using the helperNNDPDPowerAmplifier System object™.
pa = helperNNDPDPowerAmplifier(DataSource=dataSource,SampleRate=Fs); paOutputTrain = pa(txWaveTrain); paOutputVal = pa(txWaveVal); paOutputTest = pa(txWaveTest);
Preprocess data to generate input vectors containing features.
memDepth = 5; % Memory depth of the DPD (or PA model) nonlinearDegree = 5; % Nonlinear polynomial degree [inputMtxTrain,inputMtxVal,inputMtxTest,outputMtxTrain,outputMtxVal,outputMtxTest,scalingFactor] = ... helperNNDPDPreprocessData(txWaveTrain,txWaveVal,txWaveTest,paOutputTrain,paOutputVal,paOutputTest, ... memDepth,nonlinearDegree);
Implement and Train NN-DPD
Before training the neural network DPD, select the memory depth and degree of nonlinearity. For purposes of comparison, specify a memory depth of 5 and a nonlinear polynomial degree of 5, as in the Power Amplifier Characterization example. Then implement the network described in Neural Network DPD Structure section.
memDepth = 5; % Memory depth of the DPD (or PA model) nonlinearDegree = 5; % Nonlinear polynomial degree inputLayerDim = 2*memDepth+(nonlinearDegree-1)*memDepth; numNeuronsPerLayer = 30; neuronReductionRate = 0.8; lgraph = [... featureInputLayer(inputLayerDim,'Name','input') fullyConnectedLayer(numNeuronsPerLayer,'Name','linear1') leakyReluLayer(0.01,'Name','leakyRelu1') fullyConnectedLayer(round(numNeuronsPerLayer*neuronReductionRate),'Name','linear2') leakyReluLayer(0.01,'Name','leakyRelu2') fullyConnectedLayer(round(numNeuronsPerLayer*neuronReductionRate^2),'Name','linear3') leakyReluLayer(0.01,'Name','leakyRelu3') fullyConnectedLayer(2,'Name','linearOutput') ];
Train Neural Network
Train the neural network offline using the trainnet (Deep Learning Toolbox) function. First, define the training options using the trainingOptions (Deep Learning Toolbox) function and set hyperparameters. Use the Adam optimizer with a mini-batch size of 1024. The initial learning rate is 4e-4 and decreases by a factor of 0.95 every five epochs. Evaluate the training performance using validation every 10 epochs. If the validation accuracy does not increase for five validations, stop training. Use Experiment Manager (Deep Learning Toolbox) to optimize hyperparameters.
maxEpochs = 200; miniBatchSize = 1024; iterPerEpoch = floor(size(inputMtxTrain, 1)/miniBatchSize); trainingPlots ="none"; metrics =
[]; verbose =
false; options = trainingOptions('adam', ... MaxEpochs=maxEpochs, ... MiniBatchSize=miniBatchSize, ... InitialLearnRate=4e-4, ... LearnRateDropFactor=0.95, ... LearnRateDropPeriod=5, ... LearnRateSchedule='piecewise', ... Shuffle='every-epoch', ... OutputNetwork='best-validation-loss', ... ValidationData={inputMtxVal,outputMtxVal}, ... ValidationFrequency=2*iterPerEpoch, ... ValidationPatience=5, ... InputDataFormats="BC", ... TargetDataFormats="BC", ... ExecutionEnvironment='cpu', ... Plots=trainingPlots, ... Metrics = metrics, ... Verbose=verbose, ... VerboseFrequency=2*iterPerEpoch);
When running the example, you have the option of using a pretrained network by setting the trainNow variable to false. Training is desirable to match the network to your simulation configuration. If using a different PA, signal bandwidth, or target input power level, retrain the network. Training the neural network on an Intel® Xeon(R) W-2133 CPU takes about 6 minutes to satisfy the early stopping criteria specified above. Since trained network can converge to a different point then the saved data configuration, you cannot use saved data option with trainNow set to true.
trainNow =false; if trainNow netDPD = trainnet(inputMtxTrain,outputMtxTrain,lgraph,"mse",options); %#ok<UNRCH> else load('nndpdIn30Fact08'); end
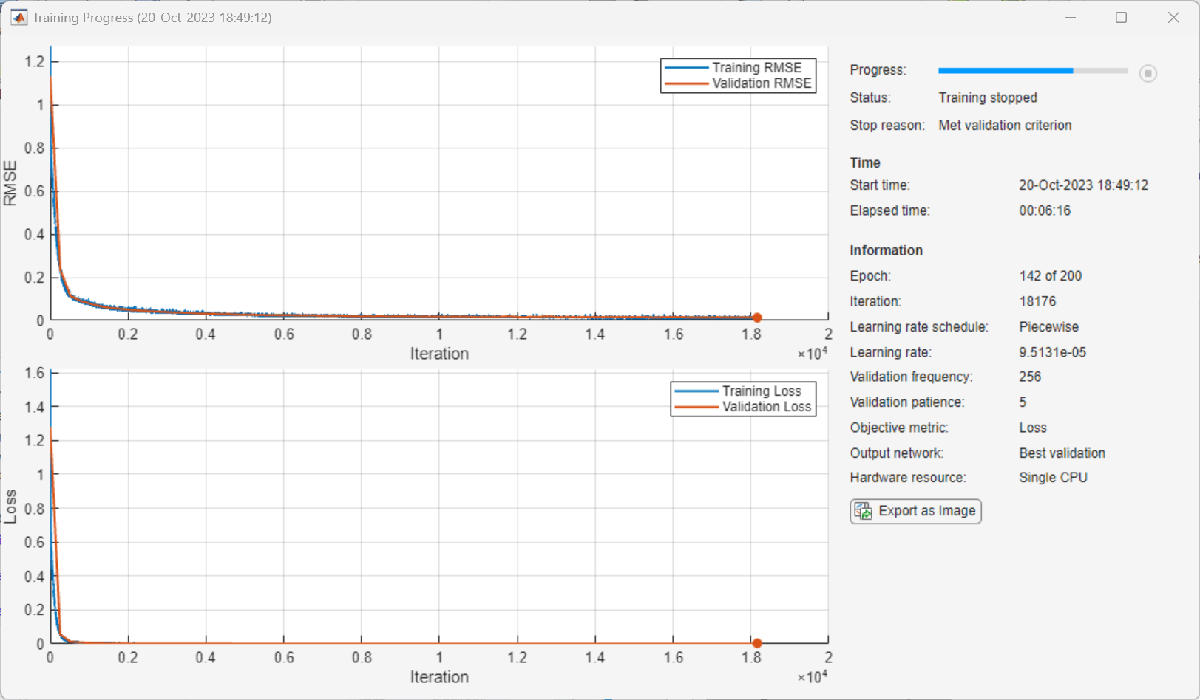
The following shows the training process with the given options. Random initialization of the weights for different layers affects the training process. To obtain the best root mean squared error (RMSE) for the final validation, train the same network a few times.
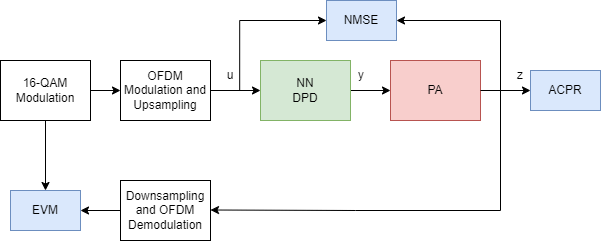
Test NN-DPD
This figure displays how to check the performance of the NN-DPD. To test the NN-DPD, pass the test signal through the NN-DPD and the PA and examine these performance metrics:
Normalized mean squared error (NMSE), measured between the input to the NN-DPD and output of the PA
Adjacent channel power ratio (ACPR), measured at the output of the PA by using the
comm.ACPRSystem objectPercent RMS error vector magnitude (EVM), measured by comparing the OFDM demodulation output to the 16-QAM modulated symbols by using the
comm.EVMSystem object
Perform these tests for both the NN-DPD and also the memory polynomial DPD described in the Digital Predistortion to Compensate for Power Amplifier Nonlinearities example.
% Pass signal through NN-DPD dpdOutNN = predict(netDPD,inputMtxTest); dpdOutNN = double(complex(dpdOutNN(:,1),dpdOutNN(:,2))); dpdOutNN = dpdOutNN/scalingFactor; paOutputNN = pa(dpdOutNN); % Pass signal through cross-term memory polynomial DPD dpdOutMP = helperNNDPDMemoryPolynomial(txWaveTest,txWaveTrain, ... paOutputTrain,nonlinearDegree,memDepth); paOutputMP = pa(dpdOutMP); % Evaluate performance with NN-DPD acprNNDPD = helperACPR(paOutputNN,Fs,bw); nmseNNDPD = helperNMSE(txWaveTest,paOutputNN); evmNNDPD = helperEVM(paOutputNN,qamRefSymTest,ofdmParams); % Evaluate the performance without DPD acprNoDPD = helperACPR(paOutputTest,Fs,bw); nmseNoDPD = helperNMSE(txWaveTest,paOutputTest); evmNoDPD = helperEVM(paOutputTest,qamRefSymTest,ofdmParams); % Evaluate the performance with memory polynomial DPD acprMPDPD = helperACPR(paOutputMP,Fs,bw); nmseMPDPD = helperNMSE(txWaveTest,paOutputMP); evmMPDPD = helperEVM(paOutputMP,qamRefSymTest,ofdmParams); % Create a table to display results evm = [evmNoDPD;evmMPDPD;evmNNDPD]; acpr = [acprNoDPD;acprMPDPD;acprNNDPD]; nmse = [nmseNoDPD;nmseMPDPD;nmseNNDPD]; disp(table(acpr,nmse,evm, ... 'VariableNames', ... {'ACPR_dB','NMSE_dB','EVM_percent'}, ... 'RowNames', ... {'No DPD','Cross-term Memory Polynomial DPD','Neural Network DPD'}))
ACPR_dB NMSE_dB EVM_percent
_______ _______ ___________
No DPD -28.674 -21.287 6.8681
Cross-term Memory Polynomial DPD -33.889 -27.984 2.8229
Neural Network DPD -38.886 -33.423 1.5679
sa = helperPACharPlotSpectrum(... [paOutputTest paOutputMP paOutputNN], ... {'No DPD','Memory Polynomial DPD', ... 'Neural Network DPD'}, ... ofdmParams.OversamplingFactor,"Modulated",[-130 -50]);
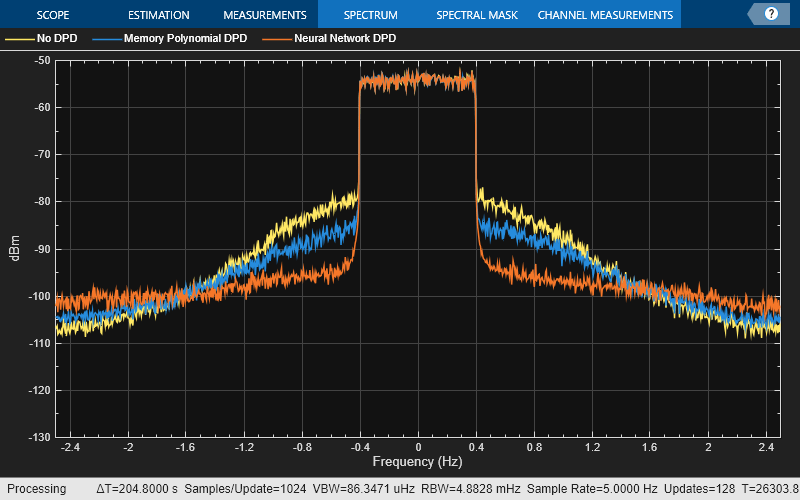
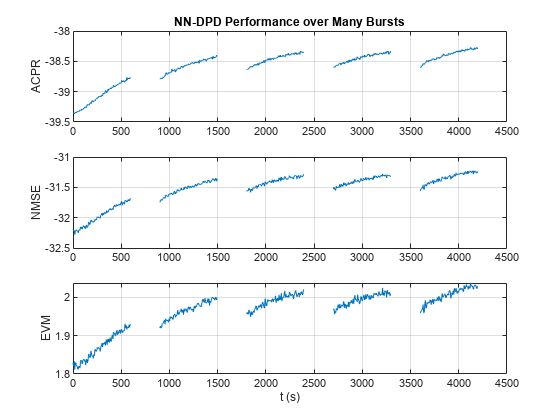
As the PA heats, the performance characteristics change. Send bursty signals through the PA repeatedly and plot system performance as a function of time. Each measurement takes about 6 s. Every 600 s, stop for 300 s to allow the PA to cool down. The plot shows that the system performance degrades with repeated use and recovers after the cooldown period. This behavior shows that after some time, the PA characteristics might change and the DPD might not provide the required system performance, such as a maximum EVM value. If the EVM value exceeds the allowed maximum value, the neural network needs to be retrained to adapt to the changing PA characteristics.
runRepeatedBurstTest =false; if strcmp(dataSource,"NI VST") && runRepeatedBurstTest numMeas = 500; measTime = 6; acprNNDPD = zeros(numMeas,1); nmseNNDPD = zeros(numMeas,1); evmNNDPD = zeros(numMeas,1); [acprLine,nmseLine,evmLine] = initFigure(); tStart = tic; cnt = 1; for p=1:numMeas % Pass signal through NN-DPD dpdOutNN = predict(netDPD,inputMtxTest); dpdOutNN = [zeros(memDepth,1);... double(complex(dpdOutNN(:,1), dpdOutNN(:,2)))]; paInput = dpdOutNN/scalingFactor; % Pass signals through PA paOutputNN = pa(paInput); % Evaluate performance with NN-DPD acprNNDPD(cnt) = helperACPR(paOutputNN,Fs,bw); nmseNNDPD(cnt) = helperNMSE(txWaveTest,paOutputNN); evmNNDPD(cnt) = helperEVM(paOutputNN,qamRefSymTest,ofdmParams); updateFigure(acprLine,nmseLine,evmLine, ... acprNNDPD(cnt),nmseNNDPD(cnt),evmNNDPD(cnt),tStart); cnt = cnt +1; if mod(p,100) == 0 for q=1:50 pause(measTime) acprNNDPD(cnt) = NaN; nmseNNDPD(cnt) = NaN; evmNNDPD(cnt) = NaN; updateFigure(acprLine,nmseLine,evmLine, ... acprNNDPD(cnt),nmseNNDPD(cnt),evmNNDPD(cnt),tStart); cnt = cnt +1; end end end else load('savedRepeatTestResultsNIVST100MHz'); figure numMeas = length(acprNNDPD); t = (0:numMeas-1)*6; subplot(3,1,1) plot(t,acprNNDPD) grid on title("NN-DPD Performance over Many Bursts") ylabel("ACPR") subplot(3,1,2) plot(t,nmseNNDPD) grid on ylabel("NMSE") subplot(3,1,3) plot(t,evmNNDPD) grid on ylabel("EVM") xlabel('t (s)') end
release(pa)
Further Exploration
This example demonstrates how to train a NN-DPD by using measured data from a PA. For the given PA, target input power level, and exciting signal, the NN-DPD is able to provide better performance than memory polynomial DPD.
You can try changing the number of neurons per layer, number of hidden layers and target input power level and see the effect of these parameters on the NN-DPD performance. You can also try different input signals, such as OFDM signals with different bandwidth. You can also generate standard-specific signals using the Wireless Waveform Generator app.
Proceed to the Neural Network for Digital Predistortion Design-Offline Training example, which shows how to train a similar network in a hardware-in-the-loop (HIL) setting using custom training loops and loss functions.
Helper Functions
helperNNDPDMemoryPolynomialhelperNNDPDPowerAmplifier
Performance Evaluation and Comparison
helperNMSEhelperACPRhelperEVM
Local Functions
Generate Oversampled OFDM Signals
Generate OFDM-based signals to excite the PA. This example uses a 5G-like OFDM waveform. Set the bandwidth of the signal to 100 MHz. Choosing a larger bandwidth signal causes the PA to introduce more nonlinear distortion and yields greater benefit from the addition of the DPD. Generate six OFDM symbols, where each subcarrier carries a 16-QAM symbol, using the helperNNDPDGenerateOFDM function. Save the 16-QAM symbols as a reference to calculate the EVM performance. To capture effects of higher order nonlinearities, the example oversamples the PA input by a factor of 5.
function [txWaveTrain,txWaveVal,txWaveTest,qamRefSymTrain,qamRefSymVal,qamRefSymTest,ofdmParams] = ... generateOversampledOFDMSignals bw = 100e6; % Hz symPerFrame = 6; % OFDM symbols per frame M = 16; % Each OFDM subcarrier contains a 16-QAM symbol osf = 5; % oversampling factor for PA input % OFDM parameters ofdmParams = helperOFDMParameters(bw,osf); % OFDM with 16-QAM in data subcarriers rng(123) [txWaveTrain,qamRefSymTrain] = helperNNDPDGenerateOFDM(ofdmParams,symPerFrame,M); [txWaveVal,qamRefSymVal] = helperNNDPDGenerateOFDM(ofdmParams,symPerFrame,M); [txWaveTest,qamRefSymTest] = helperNNDPDGenerateOFDM(ofdmParams,symPerFrame,M); end
Figure Helpers
function [acprLine,nmseLine,evmLine] = initFigure() %initFigure Initialize repeat runs figure figure subplot(3,1,1) acprLine = animatedline; grid on ylabel("ACPR (dB)") title("NN-DPD Performance Over Many Bursts") subplot(3,1,2) nmseLine = animatedline; grid on ylabel("NMSE (dB)") subplot(3,1,3) evmLine = animatedline; grid on ylabel("EVM (%)") xlabel("t (s)") end function updateFigure(acprLine,nmseLine,evmLine,acprNNDPD,nmseNNDPD,evmNNDPD,tStart) %updateFigure Update repeat runs figure addpoints(acprLine,toc(tStart),acprNNDPD) addpoints(nmseLine,toc(tStart),nmseNNDPD) addpoints(evmLine,toc(tStart),evmNNDPD) drawnow limitrate end
References
[1] Paaso, Henna, and Aarne Mammela. “Comparison of Direct Learning and Indirect Learning Predistortion Architectures.” In 2008 IEEE International Symposium on Wireless Communication Systems, 309–13. Reykjavik: IEEE, 2008. https://doi.org/10.1109/ISWCS.2008.4726067.
[2] Wang, Dongming, Mohsin Aziz, Mohamed Helaoui, and Fadhel M. Ghannouchi. “Augmented Real-Valued Time-Delay Neural Network for Compensation of Distortions and Impairments in Wireless Transmitters.” IEEE Transactions on Neural Networks and Learning Systems 30, no. 1 (January 2019): 242–54. https://doi.org/10.1109/TNNLS.2018.2838039.
See Also
Functions
featureInputLayer(Deep Learning Toolbox) |fullyConnectedLayer(Deep Learning Toolbox) |reluLayer(Deep Learning Toolbox) |trainNetwork(Deep Learning Toolbox) |trainingOptions(Deep Learning Toolbox)
Objects
comm.DPD|comm.DPDCoefficientEstimator|comm.OFDMModulator|comm.OFDMDemodulator|comm.EVM|comm.ACPR