Transfer Fcn

Lineares System als Übertragungsfunktion modellieren

• 

Bibliotheken:
Simulink / Continuous

Beschreibung

Der Block Transfer Fcn modelliert ein lineares System mithilfe einer Übertragungsfunktion der Laplace-Domänenvariable s. Der Block kann Eingrößensysteme (SISO, Single-Input Single-Output) und Mehrgrößensysteme (SIMO, Single-Input Multiple-Output) modellieren.

Bedingungen zur Verwendung dieses Blocks

Der Transfer Fcn-Block geht von den folgenden Bedingungen aus:

• Die Übertragungsfunktion hat die Form

  $$H(s)=\frac{y(s)}{u(s)}=\frac{num(s)}{den(s)}=\frac{num(1)s^{nn-1}+num(2)s^{nn-2}+\dots +num(nn)}{den(1)s^{nd-1}+den(2)s^{nd-2}+\dots +den(nd)},$$

  wobei u und y den Systemeingang bzw. die Systemausgänge darstellen und nn und nd die Anzahl der Zähler- bzw. Nennerkoeffizienten darstellen. num(s) und den(s) enthalten die Koeffizienten des Zählers und Nenners in fallenden Potenzen von s.

• Die Ordnung des Nenners muss größer gleich der Ordnung des Zählers sein.

• Bei einem Mehrgrößensystem weisen alle Übertragungsfunktionen denselben Nenner und alle Zähler dieselbe Ordnung auf.

Modellierung eines Eingrößensystems

Bei einem Eingrößensystem handelt es sich bei Eingabe und Ausgabe des Blocks um skalare Zeitsignale. Um dieses System zu modellieren:

1. Geben Sie einen Vektor für die Zählerkoeffizienten der Übertragungsfunktion in das Feld Numerator coefficients ein.

2. Geben Sie einen Vektor für die Nennerkoeffizienten der Übertragungsfunktion in das Feld Denominator coefficients ein.

Modellierung eines Mehrgrößensystems

Bei einem Mehrgrößensystem ist der Blockeingang ein Skalar und die Ausgabe ein Vektor, wobei jedes Element eine Ausgabe des Systems ist. Um dieses System zu modellieren:

1. Geben Sie eine Matrix in das Feld Numerator coefficients ein.

   Jede Zeile dieser Matrix enthält die Zählerkoeffizienten einer Übertragungsfunktion, die einen der Blockausgänge festlegt.

2. Geben Sie einen Vektor der Nennerkoeffizienten, der allen Übertragungsfunktionen des Systems gemein ist, in das Feld Denominator coefficients ein.

Anfangsbedingungen festlegen

Eine Übertragungsfunktion beschreibt die Beziehung zwischen Eingabe und Ausgabe in der Laplace-Domäne (Frequenzdomäne). Genauer gesagt ist sie als eine Laplace-Transformation der Reaktion (Ausgabe) eines Systems mit null Anfangsbedingungen auf einen Impulseinfang definiert.

Operationen der Übertragungsfunktionen, wie Multiplikation und Division, benötigen einen Anfangszustand von null. Sie können beispielsweise eine komplizierte Übertragungsfunktion in eine Reihe einfacherer Übertragungsfunktionen zerlegen. Diese können Sie sequenziell anwenden, um eine Reaktion zu erhalten, die zum Ergebnis der ursprünglichen Übertragungsfunktion identisch ist. Dies ist nicht der Fall, wenn eine der Übertragungsfunktionen einen Nicht-Null-Anfangszustand annimmt. Zudem weist eine Übertragungsfunktion unendlich viele Zeitdomänen-Realisierungen auf; die meisten diese Zustände sind physikalisch bedeutungslos.

Aus diesen Gründen setzt Simulink^® die Anfangsbedingungen des Transfer Fcn-Blocks auf null. Um Anfangsbedingungen für eine bestimmte Übertragungsfunktion festzulegen, wandeln Sie die Übertragungsfunktion mithilfe von tf2ss in eine steuerbare, kanonische Zustandsraumrealisierung um. Verwenden Sie daraufhin den State-Space-Block. Das Hilfsprogramm tf2ss stellt die Matrizen A, B, C und D für das System bereit.

Geben Sie für weitere Informationen help tf2ss ein oder ziehen Sie die Dokumentation der Control System Toolbox™ zu Rate.

Anzeige der Übertragungsfunktion auf dem Block

Der Transfer Fcn-Block zeigt die Übertragungsfunktion gemäß den von Ihnen festgelegten Zähler- und Nennerparametern an.

• Wenn Sie jeden Parameter als Ausdruck oder Vektor festlegen, zeigt dieser Block die Übertragungsfunktion mit den angegebenen Koeffizienten für die Potenzen von s an. Wenn Sie eine Variable in Klammern angeben, evaluiert der Block die Variable.

  Wenn Sie beispielsweise den Parameterwert Numerator coefficients als [3 2 1] und den Parameterwert Denominator coefficients als (den) festlegen, wobei den eine Workspace-Variable mit einem Wert von [7 5 3 1] ist, zeigt der Block die Gleichung anhand der angegebenen Werte an.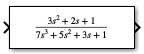

  

  Tipp

  Wenn die Blockgröße zu klein ist, um den vollständigen Zähler oder Nenner anzuzeigen, zeigt das Blocksymbol den Zähler als num(s) und den Nenner als den(s) an.

  

  Wenn der Block die Gleichung für die vom Block implementierte Übertragungsfunktion anzeigen soll, ziehen Sie eine Ecke des Blocks, um dessen Größe zu ändern.

  

• Wenn Sie jeden Parameter als Variable angeben, zeigt der Block den Namen der Variable an, gefolgt von (s).

  Wenn Sie beispielsweise für den Parameter Numerator coefficients num und für den Parameter Denominator coefficients den angeben, zeigt das Blocksymbol für den Zähler der Übertragungsfunktion num(s) und für den Nenner den(s) an.

  

Beispiele

Aircraft Longitudinal Flight Control

Model flight control for the longitudinal motion of an aircraft using first-order linear approximations.

• Modell öffnen

Model an Anti-Lock Braking System

Model a simple Anti-Lock Braking System (ABS). The model simulates the dynamic behavior of a vehicle under hard braking conditions. The model represents a single wheel, which may be replicated a number of times to create a model for a multi-wheel vehicle.

• Modell öffnen

Invertiertes Pendel mit Animation

Dieses Beispiel zeigt, wie Simulink® zur Modellierung und Animation eines invertierten Pendelsystems verwendet werden kann. Bei einem invertierten Pendel liegt der Schwerpunkt über dem Drehpunkt. Um diese Position stabil zu halten, implementiert das System eine Steuerlogik, um den Drehpunkt unter den Schwerpunkt zu bewegen, wenn das Pendel abzufallen beginnt. Das invertierte Pendel ist ein klassisches dynamisches Problem, das zur Prüfung von Kontrollstrategien verwendet wird.

• Modell öffnen

Ports

Eingabe

Port_1 — Eingangssignal

Skalar

Eingangssignal, angegeben als Skalar mit dem Datentyp double.

Dieser Port hat nur eine direkte Durchleitung, wenn der Zähler der Übertragungsfunktion 0 ist.

Datentypen: double

Ausgabe

Port_1 — Ausgangssignal

Skalar | Vektor

Ausgangssignal, angegeben als Skalar oder Vektor mit dem Datentyp double.

• Bei einem Eingrößensystem handelt es sich bei Eingabe und Ausgabe des Blocks um skalare Zeitsignale.

• Bei einem Mehrgrößensystem ist die Eingabe ein Skalar und die Ausgabe ein Vektor, wobei jedes Element eine Ausgabe des Systems ist.

Datentypen: double

Parameter

Numerator coefficients — Vektor oder Matrix aus Zählerkoeffizienten

[1] (Standardeinstellung) | Vektor | Matrix

Legt die Zählerkoeffizienten der Übertragungsfunktion fest.

• Geben Sie bei einem Eingrößensystem die Zählerkoeffizienten der Übertragungsfunktion als Vektor an.

• Geben Sie bei einem Mehrgrößensystem eine Matrix an. Jede Zeile dieser Matrix enthält die Zählerkoeffizienten einer Übertragungsfunktion, die einen der Blockausgänge festlegt.

Programmatische Verwendung

Blockparameter: Numerator

Typ: Zeichenvektor, String

Werte: Vektor | Matrix

Standardwert: '[1]'

Denominator coefficients — Zeilenvektor der Nennerkoeffizienten

[1 1] (Standardeinstellung) | Vektor

Legt den Zeilenvektor der Nennerkoeffizienten fest.

• Geben Sie bei einem Eingrößensystem die Nennerkoeffizienten der Übertragungsfunktion als Vektor an.

• Geben Sie bei einem Mehrgrößensystem einen Vektor an, der die Nennerkoeffizienten enthält, die allen Übertragungsfunktionen des Systems gemein sind.

Programmatische Verwendung

Blockparameter: Denominator

Typ: Zeichenvektor | String

Werte: Vektor

Standardwert: '[1 1]'

Parameter tunability — Abstimmbare Darstellung der Blockparameter in Code

Auto (Standardeinstellung) | Optimized | Unconstrained

Abstimmbarkeit der Zähler- und Nennerkoeffizienten für beschleunigte Simulationsmodi und bereitgestellte Simulationen mit Simulink Compiler™. Setzen Sie diesen Parameter auf Auto, um Simulink die angemessene Parameter-Abstimmbarkeit wählen zu lassen.

Setzen Sie diesen Parameter auf Optimized, um eine für bessere Simulationsleistung optimierte Darstellung der Zähler- und Nennerkoeffizienten in generiertem Code für beschleunigte und bereitgestellte Simulationen zu erzeugen.

Setzen Sie diesen Parameter auf Unconstrained, um eine (zwischen Simulationen) vollständig abstimmbare Darstellung der Zähler- und Nennerkoeffizienten in generiertem Code für beschleunigte und bereitgestellte Simulationen zu erzeugen. Wählen Sie Auto, um Simulink die angemessene Abstimmbarkeit wählen zu lassen.

Programmatische Verwendung

Blockparameter: ParameterTunability

Typ: Zeichenvektor, String

Werte: 'Auto' | 'Optimized' | 'Unconstrained'

Standardwert: 'Auto'

Absolute tolerance — Absolute Toleranz für die Berechnung von Blockzuständen

auto (Standardeinstellung) | Skalar | Vektor

Solver mit variablen Schritten verwenden absolute und relative Toleranzen bei der Auswahl der Schrittgröße, um zu ermitteln, ob der Fehler in Zustandsberechnungen akzeptabel ist.

Um die absolute Toleranz aus dem Konfigurationsparameter Absolute tolerance zu übernehmen, geben Sie für diesen Parameterwert auto oder -1 an.

Um für diesen Block eine absolute Toleranz festzulegen, die den im Konfigurationsparameter Absolute tolerance festlegten Wert übersteuert:

• Geben Sie einen reellen, positiven Skalarwert an, der für die Berechnung aller Blockzustände verwendet werden soll.

• Geben Sie einen reellen Vektor mit Dimensionen an, die den Dimensionen der kontinuierlichen Zustände des Blocks entsprechen.

Programmatische Verwendung

Um den Wert des Blockparameters programmatisch festzulegen, verwenden Sie die Funktion set_param.

Um den Wert des Blockparameters programmatisch abzurufen, verwenden Sie die Funktion get_param.

Parameter:	AbsoluteTolerance
Werte:	'auto' (Standardeinstellung) | '-1' | positive real scalar number | vector of positive real scalar numbers
Datentypen:	char | string

Beispiel: set_param("MyModel/Descriptor State-Space",AbsoluteTolerance="-1")

State Name (e.g., 'position') — Option zum Zuweisen eindeutiger Namen zu Zuständen

'' (Standardeinstellung) | Zeichenvektor | Zell-Array von Zeichenvektoren | MATLAB^®-Variable | ...

Verwenden Sie diesen Parameter, um den Zuständen dieses Blocks optional Namen zuzuweisen. Die von Ihnen zugewiesenen Namen gelten nur für die Zustände dieses Blocks.

• Lassen Sie dieses Feld leer (''), um die Standard-Zustandsnamen zu verwenden.

• Um einem Zustand einen Namen zuzuweisen, geben Sie den Namen in Anführungszeichen ein. Geben Sie beispielsweise 'position' ein, um einen Zustand mit position zu benennen.

• Um Namen mehreren Zuständen zuzuweisen, geben Sie diesen Parameterwert als Zellenarray aus Zeichenvektoren an. Jeder Name im Zellenarray muss eindeutig sein. Geben Sie beispielsweise {'a','b','c'} ein, um die Namen a, b und c zuzuweisen.

• Um die Namen mithilfe einer MATLAB-Variable anzugeben, geben Sie den Namen der Variable ohne Anführungszeichen ein. Geben Sie beispielsweise names ein, um die Zustandsnamen mithilfe der Variable names anzugeben.

Sie können eine Anzahl von Namen angeben, die kleiner als die Anzahl der Zustände des Blocks ist. In diesem Fall werden die Zustandsnamen für mehrere Zustände verwendet und die Anzahl der Zustände muss glatt auf die Anzahl der Zustandsnamen aufteilbar sein. Wenn Sie beispielsweise zwei Namen für einen Block mit vier Zuständen angeben, wird der erste Name für die ersten zwei Zustände und der zweite Name für die letzten zwei Zustände verwendet.

Programmatische Verwendung

Um den Wert des Blockparameters programmatisch festzulegen, verwenden Sie die Funktion set_param.

Um den Wert des Blockparameters programmatisch abzurufen, verwenden Sie die Funktion get_param.

Parameter:	ContinuousStateAttributes
Werte:	'' (Standardeinstellung) | valid MATLAB variable name
Datentypen:	char | string | cell

Beispiel: set_param("MyModel/Descriptor State-Space",ContinuousStateAttributes={'position','velocity'})

Blockeigenschaften

Datentypen	double
Direct Feedthrough	neina
Mehrdimensionale Signale	nein
Signale mit variabler Größe	nein
Erkennung von Nulldurchgängen	nein
a Die Direktdurchführungseigenschaften für diesen Block hängen von den Blockparameterwerten ab.

Erweiterte Fähigkeiten

C/C++ Codegenerierung

Generieren von C und C++ Code mit Simulink® Coder™.

Nicht für Produktionscode empfohlen. Steht in Zusammenhang mit Ressourcengrenzen und Begrenzungen hinsichtlich Geschwindigkeit und Speicher, die oft bei eingebetteten Systemen bestehen. Der generierte Code kann dynamische Zuweisung und Freigebung von Speicher, Rekursion, zusätzlichen Speicherbedarf und stark schwankende Ausführungszeiten umfassen. Der Code ist zwar funktional gültig und in ressourcenreichen Umgebungen allgemein akzeptiert, aber kleinere eingebettete Zielsysteme können solchen Code oft nicht unterstützen.

Im Allgemeinen könnte empfehlenswert sein, den Simulink Model Discretizer zu verwenden, um kontinuierliche Blöcke in diskreten Äquivalenten abzubilden, die eine Generierung von Produktionscode unterstützen. Um den Model Discretizer zu starten, klicken Sie im Simulink Editor auf der Registerkarte Apps unter Apps unter Control Systems auf Model Discretizer. Eine Ausnahme ist der Block Second-Order Integrator, da bei diesem Block der Model Discretizer eine angenäherte Diskretisierung erzeugt.

Versionsverlauf

Eingeführt vor R2006a

Siehe auch

Discrete Transfer Fcn | State-Space

Themen

• State