Grenzwertprobleme
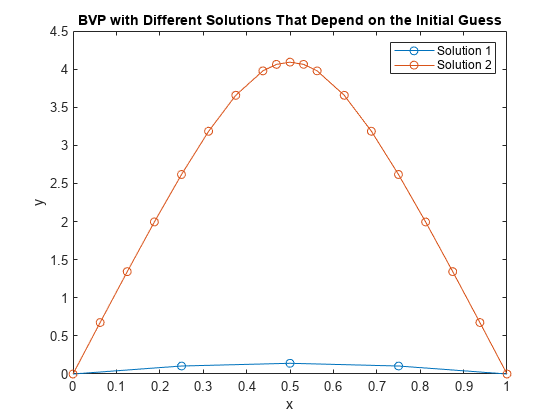
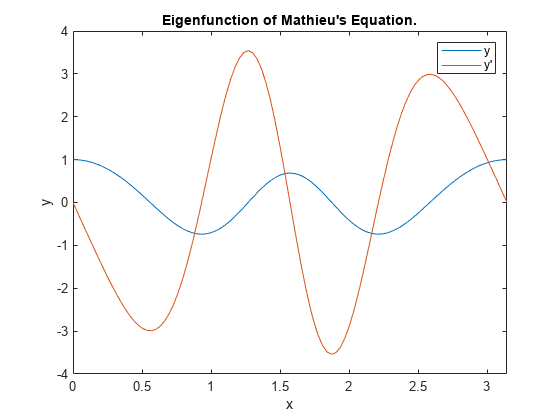
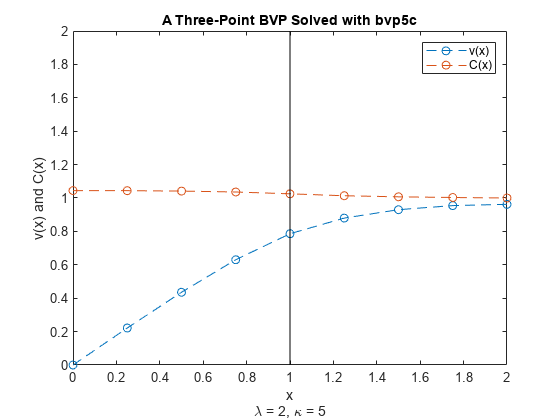
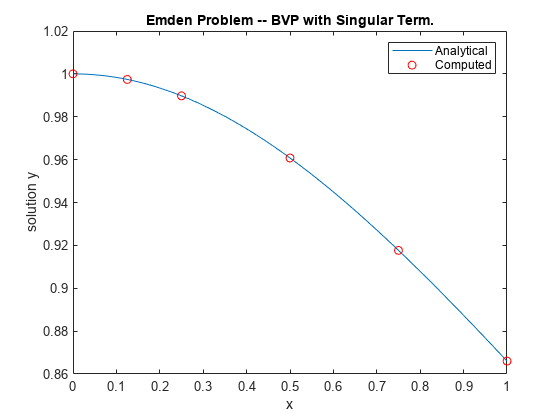
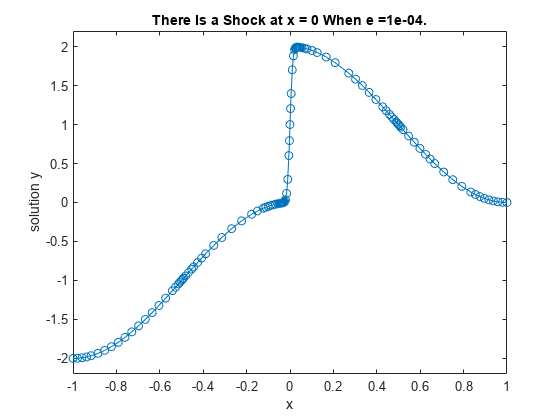
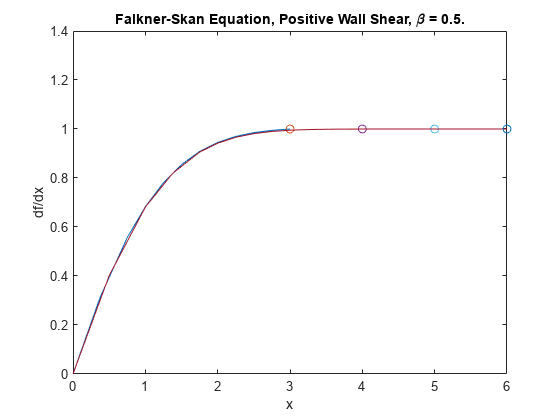
Grenzwertprobleme sind gewöhnliche Differenzialgleichungen, die Grenzbedingungen unterliegen. Anders als bei Ausgangswertproblemen kann es bei Grenzwertproblemen eine endliche Lösung, keine Lösung oder unendlich viele Lösungen geben. Die ursprüngliche Schätzung der Lösung ist wesentlicher Bestandteil der Lösung eines Grenzwertproblems, dabei kann die Qualität der Schätzung über die Leistung des Solvers oder gar über eine erfolgreiche Berechnung entscheiden. Die Solver bvp4c und bvp5c funktionieren bei Grenzwertproblemen mit Zwei- oder Mehrpunkt-Grenzbedingungen, Singularitäten in den Lösungen oder unbekannten Parametern. Weitere Informationen finden Sie unter Solving Boundary Value Problems.
Funktionen
Themen
- Solving Boundary Value Problems
Background information, solver capabilities and algorithms, and example summary.