bvp5c
Solve boundary value problem — fifth-order method
Description
sol = bvp5c(odefun,bcfun,solinit)odefun, subject to the boundary conditions
described by bcfun and the initial solution guess
solinit. Use the bvpinit function to create the initial guess solinit, which
also defines the points at which the boundary conditions in bcfun are
enforced.
sol = bvp5c(odefun,bcfun,solinit,options)options, which is an
argument created using the bvpset function. For example, use the
AbsTol and RelTol options to specify absolute and
relative error tolerances, or the FJacobian option to provide the
analytical partial derivatives of odefun.
Examples
Solve a second-order BVP in MATLAB® using functions. For this example, use the second-order equation
.
The equation is defined on the interval subject to the boundary conditions
,
.
To solve this equation in MATLAB, you need to write a function that represents the equation as a system of first-order equations, a function for the boundary conditions, and a function for the initial guess. Then the BVP solver uses these three inputs to solve the equation.
Code Equation
Write a function that codes the equation. Use the substitutions and to rewrite the equation as a system of first-order equations.
,
.
The corresponding function is
function dydx = bvpfcn(x,y) dydx = zeros(2,1); dydx = [y(2) -y(1)]; end
Note: All functions are included at the end of the example as local functions.
Code Boundary Conditions
Write a function that codes the boundary conditions in the form . In this form the boundary conditions are
,
.
The corresponding function is
function res = bcfcn(ya,yb) res = [ya(1) yb(1)-2]; end
Create Initial Guess
Use the bvpinit function to create an initial guess for the solution of the equation. Since the equation relates to , a reasonable guess is that the solution involves trigonometric functions. Use a mesh of five points in the interval of integration. The first and last values in the mesh are where the solver applies the boundary conditions.
The function for the initial guess accepts as an input and returns a guess for the value of and . The function is
function g = guess(x) g = [sin(x) cos(x)]; end
xmesh = linspace(0,pi/2,5); solinit = bvpinit(xmesh, @guess);
Solve Equation
Use bvp5c with the derivative function, boundary condition function, and initial guess to solve the problem.
sol = bvp5c(@bvpfcn, @bcfcn, solinit);
Plot Solution
plot(sol.x, sol.y, '-o')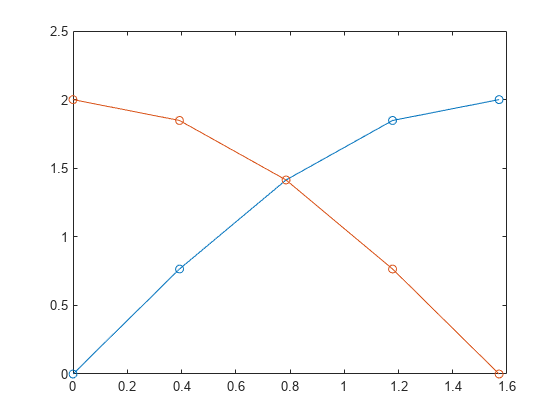
Local Functions
Listed here are the local functions that bvp5c uses to solve the equation.
function dydx = bvpfcn(x,y) % equation to solve dydx = zeros(2,1); dydx = [y(2) -y(1)]; end %-------------------------------- function res = bcfcn(ya,yb) % boundary conditions res = [ya(1) yb(1)-2]; end %-------------------------------- function g = guess(x) % initial guess for y and y' g = [sin(x) cos(x)]; end %--------------------------------
Solve a BVP at a crude error tolerance with two different solvers and compare the results.
Consider the second-order ODE
.
The equation is defined on the interval subject to the boundary conditions
,
.
To solve this equation in MATLAB®, you need to write a function that represents the equation as a system of first-order equations, write a function for the boundary conditions, set some option values, and create an initial guess. Then the BVP solver uses these four inputs to solve the equation.
Code Equation
With the substitutions and , you can rewrite the ODE as a system of first-order equations
,
.
The corresponding function is
function dydx = bvpfcn(x,y) dydx = [y(2) -2*y(2)/x - y(1)/x^4]; end
Note: All functions are included at the end of the example as local functions.
Code Boundary Conditions
The boundary condition function requires that the boundary conditions are in the form . In this form, the boundary conditions are
,
.
The corresponding function is
function res = bcfcn(ya,yb) res = [ya(1) yb(1)-sin(1)]; end
Set Options
Use bvpset to turn on the display of solver statistics, and specify crude error tolerances to highlight the difference in error control between the solvers. Also, for efficiency, specify the analytical Jacobian
.
The corresponding function that returns the value of the Jacobian is
function dfdy = jac(x,y) dfdy = [0 1 -1/x^4 -2/x]; end
opts = bvpset('FJacobian',@jac,'RelTol',0.1,'AbsTol',0.1,'Stats','on');
Create Initial Guess
Use bvpinit to create an initial guess of the solution. Specify a constant function as the initial guess with an initial mesh of 10 points in the interval .
xmesh = linspace(1/(3*pi), 1, 10); solinit = bvpinit(xmesh, [1; 1]);
Solve Equation
Solve the equation with both bvp4c and bvp5c.
sol4c = bvp4c(@bvpfcn, @bcfcn, solinit, opts);
The solution was obtained on a mesh of 9 points. The maximum residual is 9.794e-02. There were 157 calls to the ODE function. There were 28 calls to the BC function.
sol5c = bvp5c(@bvpfcn, @bcfcn, solinit, opts);
The solution was obtained on a mesh of 11 points. The maximum error is 6.742e-02. There were 244 calls to the ODE function. There were 29 calls to the BC function.
Plot Results
Plot the results of the two calculations for with the analytic solution for comparison. The analytic solution is
,
.
xplot = linspace(1/(3*pi),1,200); yplot = [sin(1./xplot); -cos(1./xplot)./xplot.^2]; plot(xplot,yplot(1,:),'k',sol4c.x,sol4c.y(1,:),'r*',sol5c.x,sol5c.y(1,:),'bo') title('Comparison of BVP Solvers with Crude Error Tolerance') legend('True','BVP4C','BVP5C') xlabel('x') ylabel('solution y')
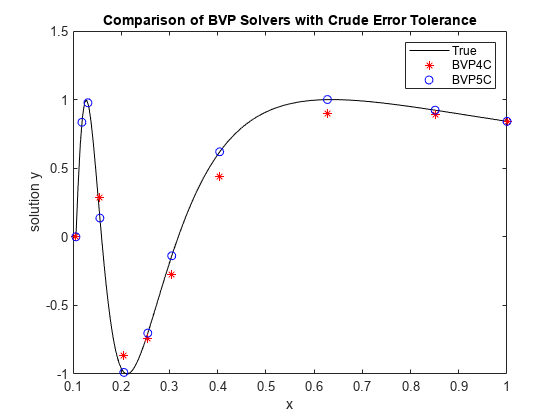
The plot confirms that bvp5c directly controls the true error in the calculation, while bvp4c controls it only indirectly. At more stringent error tolerances, this difference between the solvers is not as apparent.
Local Functions
Listed here are the local functions that the BVP solvers use to solve the problem.
function dydx = bvpfcn(x,y) % equation to solve dydx = [y(2) -2*y(2)/x - y(1)/x^4]; end %--------------------------------- function res = bcfcn(ya,yb) % boundary conditions res = [ya(1) yb(1)-sin(1)]; end %--------------------------------- function dfdy = jac(x,y) % analytical jacobian for f dfdy = [0 1 -1/x^4 -2/x]; end %---------------------------------
Input Arguments
Functions to solve, specified as a function handle that defines the functions to be
integrated. odefun and bcfun must accept the same
number of input arguments.
To code odefun, use the functional signature dydx =
odefun(x,y) for a scalar x and column vector
y. The return value dydx is a column vector of
data type single or double that corresponds to f(x,y). odefun must accept both input arguments
x and y, even if one of the arguments is not
used in the function.
For example, to solve , use the function:
function dydx = odefun(x,y) dydx = 5*y-3; end
For a system of equations, the output of odefun is a vector. Each
element in the vector is the solution to one equation. For example, to solve
use the function:
function dydx = odefun(x,y) dydx = zeros(2,1); dydx(1) = y(1)+2*y(2); dydx(2) = 3*y(1)+2*y(2); end
bvp5c also can solve problems with singularities in the
solution or multipoint boundary
conditions.
Example: sol = bvp5c(@odefun, @bcfun, solinit)
Unknown Parameters
If the BVP being solved includes unknown parameters, you instead can use the
functional signature dydx = odefun(x,y,p), where
p is a vector of parameter values. When you use this functional
signature the BVP solver calculates the values of the unknown parameters starting from
the initial guess for the parameter values provided in
solinit.
Data Types: function_handle
Boundary conditions, specified as a function handle that computes the residual error
in the boundary conditions. odefun and bcfun must
accept the same number of input arguments.
To code bcfun, use the functional signature res =
bcfun(ya,yb) for column vectors ya and
yb. The return value res is a column vector of
data type single or double that corresponds to the
residual value of the boundary conditions at the boundary points.
For example, if y(a) = 1 and y(b) = 0, then the boundary condition function is
function res = bcfun(ya,yb)
res = [ya(1)-1
yb(1)];
endya(1)-1 should
be 0 at the point x = a. Similarly, since
y(b) = 0, the residual value of yb(1) should be
0 at the point x = b.The boundary points x = a and x = b where the
boundary conditions are enforced are defined in the initial guess structure
solinit. For two-point boundary value problems, a =
solinit.x(1) and b = solinit.x(end).
Example: sol = bvp5c(@odefun, @bcfun, solinit)
Unknown Parameters
If the BVP being solved includes unknown parameters, you instead can use the
functional signature res = bcfun(ya,yb,p), where
p is a vector of parameter values. When you use this functional
signature the BVP solver calculates the values of the unknown parameters starting from
the initial guess for the parameter values provided in
solinit.
Data Types: function_handle
Initial guess of solution, specified as a structure. Use bvpinit to create solinit.
Unlike initial value problems, a boundary value problem can have no solution, a finite number of solutions, or infinitely many solutions. An important part of the process of solving a BVP is providing a guess for the required solution. The quality of this guess can be critical for the solver performance and even for a successful computation. For some guidelines on creating a good initial guess, see Initial Guess of Solution.
Example: sol = bvp5c(@odefun, @bcfun, solinit)
Data Types: struct
Option structure. Use the bvpset function to create or modify the
options structure.
Example: options = bvpset('RelTol',1e-5,'Stats','on') specifies a
relative error tolerance of 1e-5 and turns on the display of solver
statistics.
Data Types: struct
Output Arguments
Solution structure. You can access the fields in sol with
dot-indexing, such as sol.field1. The solution
(sol.x,sol.y) is continuous on the interval of
integration defined in the initial mesh solinit.x and has a
continuous first derivative there. You can use sol with the deval function to evaluate the solution at other points in the
interval.
The structure sol has these fields.
| Field | Description |
|---|---|
| Mesh selected by |
| Approximation to y(x) at the mesh points of
|
| Approximation to y′(x) at the mesh points of
|
| Final values for the unknown parameters specified in
|
|
|
| Computational cost statistics related to the solution: the number
of mesh points, residual error, and number of calls to
|
More About
For multipoint boundary value problems, the boundary conditions are enforced at several points in the interval of integration.
bvp5c can solve multipoint boundary value problems where a = a0 < a1 < a2 < ...< an = b are boundary points in the interval
[a,b]. The points a1,a2,...,an−1 represent interfaces that divide
[a,b] into regions. bvp5c
enumerates the regions from left to right (from a to
b), with indices starting from 1. In region k,
[ak−1,ak],
bvp5c evaluates the derivative as
yp = odefun(x,y,k)
In the boundary conditions function bcfun(yleft,yright),
yleft(:,k) is the solution at the left boundary of
[ak−1,ak].
Similarly, yright(:,k) is the solution at the right boundary of region
k. In particular, yleft(:,1) = y(a) and
yright(:,end) = y(b).
When you create an initial guess with bvpinit, use double entries
in xinit for each interface point. See the reference page for bvpinit for more information.
If yinit is a function, bvpinit calls y
= yinit(x,k) to get an initial guess for the solution at x in
region k. In the solution structure sol returned by
bpv4c, sol.x has double entries for each interface
point. The corresponding columns of sol.y contain the left and right
solution at the interface, respectively.
See Solve BVP with Multiple Boundary Conditions for an example that solves a three-point boundary value problem.
bvp5c solves a class of singular boundary value
problems, including problems with unknown parameters p, of the
form
The interval is required to be [0, b] with b >
0. Often such problems arise when computing a smooth solution of ODEs that result from
partial differential equations (PDEs) due to cylindrical or spherical symmetry. For singular
problems, you specify the (constant) matrix S as the value of the
'SingularTerm' option of bvpset, and odefun evaluates only
f(x,y,p). The
boundary conditions and initial guess must be consistent with the necessary condition for
smoothness S·y(0) = 0.
See Solve BVP with Singular Term for an example that solves a singular boundary value problem.
Algorithms
bvp5c is a finite difference code that implements the four-stage
Lobatto IIIa formula [1]. This is a collocation formula and the collocation polynomial
provides a C1-continuous solution that is
fifth-order accurate uniformly in [a,b]. The formula is implemented as an
implicit Runge-Kutta formula. Some of the differences between bvp5c and
bvp4c are:
bvp5csolves the algebraic equations directly.bvp4cuses analytical condensation.bvp4chandles unknown parameters directly.bvp5caugments the system with trivial differential equations for the unknown parameters.
References
[1] Shampine, L.F., and J. Kierzenka. "A BVP Solver that Controls Residual and Error." J. Numer. Anal. Ind. Appl. Math. Vol. 3(1-2), 2008, pp. 27–41.
Extended Capabilities
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
Version History
Introduced in R2006b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)