rlocus
Wurzelortskurve dynamischer Systeme
Beschreibung
rlocus( berechnet den Wurzelort des SISO-Modells sys)sys und stellt ihn in einem Diagramm dar. Der Wurzelort liefert die Polbahnen des geschlossenen Regelkreises in Abhängigkeit von der Feedback-Verstärkung k (unter der Annahme eines negativen Feedbacks). Die Wurzelorte werden verwendet, um die Auswirkungen unterschiedlicher Feedback-Verstärkungsfaktoren auf die Polstellen des geschlossenen Regelkreises zu untersuchen. Diese Orte wiederum liefern indirekte Informationen über das Zeitverhalten und die Frequenzgänge.
Sie können rlocus verwenden, um das Wurzelortsdiagramm einer der folgenden negativen Feedback-Schleifen darzustellen, indem Sie sys wie folgt festlegen:

Wenn sys beispielsweise eine Transferfunktion ist, die durch
dargestellt ist, sind die Polstellen eines geschlossenen Regelkreises die Wurzeln von
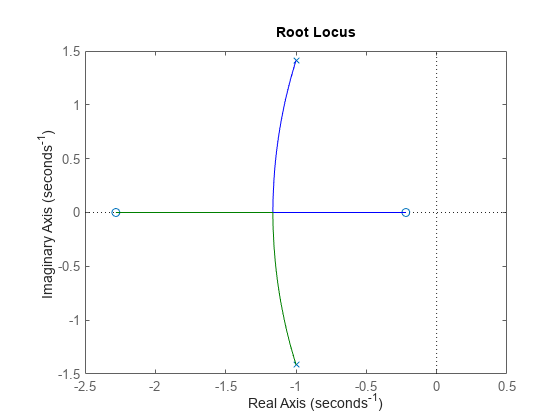
Die Wurzelortskurve zeigt die Trajektorien der Polstellen des geschlossenen Regelkreises, wenn die Feedback-Verstärkung k von 0 bis unendlich variiert. rlocus wählt adaptiv eine Reihe positiver Verstärkungsfaktoren k aus, um eine glatte Kurve zu erzeugen. Die Polstellen in der Wurzelortskurve werden mit x und die Nullstellen mit o bezeichnet.
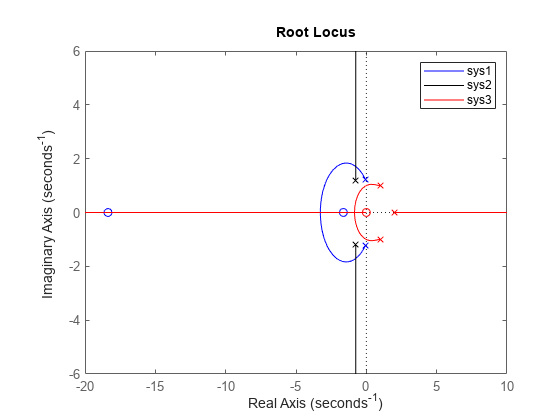
rlocus(sys1,sys2,...) stellt die Wurzelorte mehrerer LTI-Modelle sys1, sys2,... in einem einzigen Diagramm dar. Sie können für jedes Modell eine Farbe, einen Linienstil und eine Marke festlegen. Weitere Informationen zu den Anpassungsmöglichkeiten von Diagrammen finden Sie unter rlocusplot.
Beispiele
Eingabeargumente
Ausgangsargumente
Tipps
Informationen zu einem interaktiven Ansatz für die Darstellung von Wurzelorten finden Sie unter Control System Designer.
Versionsverlauf
Eingeführt vor R2006a
Siehe auch
rlocusplot | tf | pole | zero | ss | zpk | Control System Designer