CI Core Engine
Compression-ignition engine from intake to exhaust port
Libraries:
Powertrain Blockset /
Propulsion /
Combustion Engine Components /
Core Engine
Description
The CI Core Engine block implements a compression-ignition (CI) engine from intake to the exhaust port. You can use the block for hardware-in-the-loop (HIL) engine control design or vehicle-level fuel economy and performance simulations.
The CI Core Engine block calculates:
Brake torque
Exhaust temperature
Air-fuel ratio (AFR)
Fuel rail pressure
Engine-out (EO) exhaust emissions:
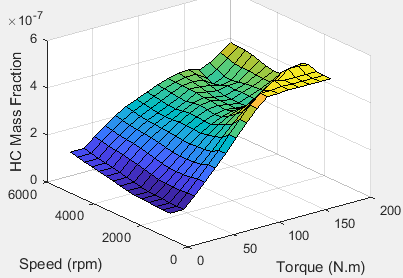
Hydrocarbon (HC)
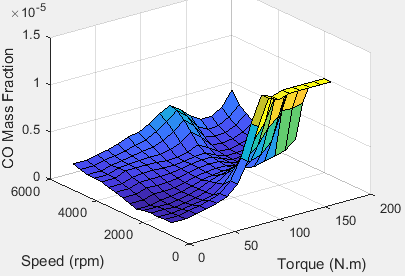
Carbon monoxide (CO)
Nitric oxide and nitrogen dioxide (NOx)
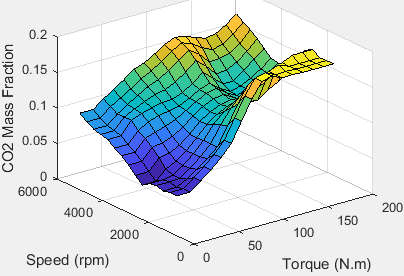
Carbon dioxide (CO2)
Particulate matter (PM)
Air Mass Flow
To calculate the air mass flow, the compression-ignition (CI) engine uses the CI Engine Speed-Density Air Mass Flow Model. The speed-density model uses the speed-density equation to calculate the engine air mass flow, relating the engine intake port mass flow to the intake manifold pressure, intake manifold temperature, and engine speed.
Brake Torque
To calculate the engine torque, you can configure the block to use either of these torque models.
| Brake Torque Model | Description |
|---|---|
| CI Engine Torque Structure Model |
The CI core engine torque structure model determines the engine torque by reducing the maximum engine torque potential as these engine conditions vary from nominal:
To account for the effect of post-inject fuel on torque, the model uses a calibrated torque offset table. |
| CI Engine Simple Torque Model | For the simple engine torque calculation, the CI engine uses a torque lookup table map that is a function of engine speed and injected fuel mass. |
Fuel Flow
In the CI Core Engine and CI Controller blocks, you can represent multiple injections with the start of injection (SOI) and fuel mass inputs to the model. To specify the type of injection, use the Fuel mass injection type identifier parameter.
| Type of Injection | Parameter Value |
|---|---|
Pilot |
|
Main |
|
Post |
|
Passed |
|
The model considers Passed fuel injections and fuel injected
later than a threshold to be unburned fuel. Use the Maximum start of injection angle
for burned fuel, f_tqs_f_burned_soi_limit parameter to specify the
threshold.
To calculate the engine fuel mass flow, the CI Core Engine block uses fuel mass flow delivered by the injectors and the engine airflow.
To calculate the fuel economy for high-fidelity models, the block uses the volumetric fuel flow.
The equation uses these variables.
| Fuel mass flow, g/s | |
| mfuel,inj | Fuel mass per injection |
Crankshaft revolutions per power stroke, rev/stroke | |
Number of engine cylinders | |
| N | Engine speed, rpm |
| Qfuel | Volumetric fuel flow |
| Sgfuel | Specific gravity of fuel |
The block uses the internal signal FlwDir to track the direction of the flow.
Air-Fuel Ratio
To calculate the air-fuel (AFR) ratio, the CI Core Engine and SI Core Engine blocks implement this equation.
The CI Core Engine uses this equation to calculate the relative AFR.
To calculate the exhaust gas recirculation (EGR), the blocks implement this equation. The calculation expresses the EGR as a percent of the total intake port flow.
The equations use these variables.
Air-fuel ratio | |
| AFRs | Stoichiometric air-fuel ratio |
Engine air mass flow | |
Fuel mass flow | |
λ | Relative AFR |
| yintk,b | Intake burned mass fraction |
| EGRpct | EGR percent |
Recirculated burned gas mass flow rate |
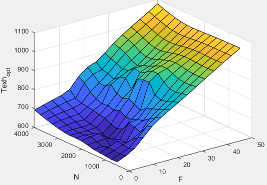
Exhaust Temperature
The exhaust temperature calculation depends on the torque model. For both torque models, the block implements lookup tables.
Torque Model | Description | Equations |
|---|---|---|
| Exhaust temperature lookup table is a function of the injected fuel mass and engine speed. |
|
Torque Structure |
The nominal exhaust temperature, Texhnom, is a product of these exhaust temperature efficiencies:
The exhaust temperature, Texhnom, is offset by a post temperature effect, ΔTpost, that accounts for post and late injections during the expansion and exhaust strokes. |
|
The equations use these variables.
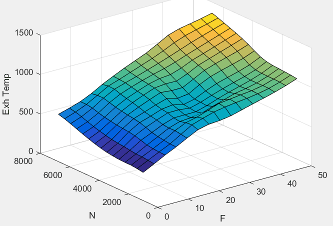
F | Compression stroke injected fuel mass |
N | Engine speed |
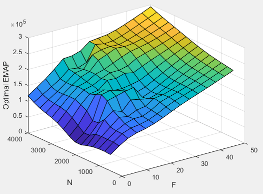
Texh | Exhaust manifold gas temperature |
Texhopt | Optimal exhaust manifold gas temperature |
| ΔTpost | Post injection temperature effect |
| Texhnom | Nominal exhaust temperature |
SOIexhteff | Main SOI exhaust temperature efficiency multiplier |
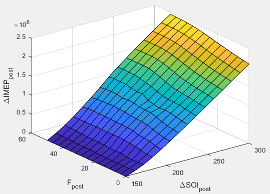
ΔSOI | Main SOI timing relative to optimal timing |
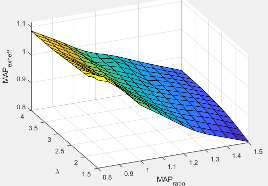
MAPexheff | Intake manifold gas pressure exhaust temperature efficiency multiplier |
MAPratio | Intake manifold gas pressure ratio relative to optimal pressure ratio |
λ | Intake manifold gas lambda |
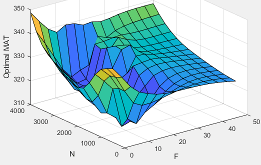
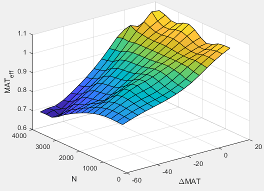
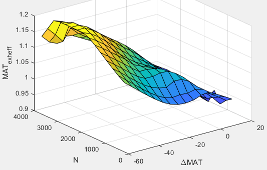
MATexheff | Intake manifold gas temperature exhaust temperature efficiency multiplier |
ΔMAT | Intake manifold gas temperature relative to optimal temperature |
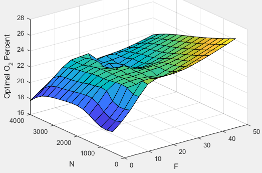
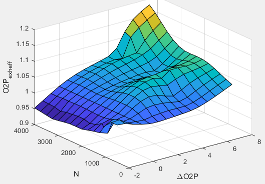
O2Pexheff | Intake manifold gas oxygen exhaust temperature efficiency multiplier |
ΔO2P | Intake gas oxygen percent relative to optimal |
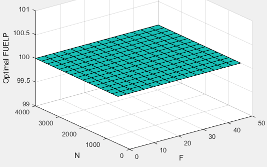
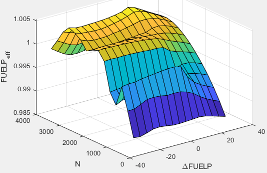
FUELPexheff | Fuel rail pressure exhaust temperature efficiency multiplier |
ΔFUELP | Fuel rail pressure relative to optimal |
EO Exhaust Emissions
The block calculates these engine-out (EO) exhaust emissions:
Hydrocarbon (HC)
Carbon monoxide (CO)
Nitric oxide and nitrogen dioxide (NOx)
Carbon dioxide (CO2)
Particulate matter (PM)
The exhaust temperature determines the specific enthalpy.
The exhaust mass flow rate is the sum of the intake port air mass flow and the fuel mass flow.
To calculate the exhaust emissions, the block multiplies the emission mass fraction by the exhaust mass flow rate. To determine the emission mass fractions, the block uses lookup tables that are functions of the engine torque and speed.
The fraction of air and fuel entering the intake port, injected fuel, and stoichiometric AFR determine the air mass fraction that exits the exhaust.
If the engine is operating at the stoichiometric or fuel rich AFR, no air exits the exhaust. Unburned hydrocarbons and burned gas comprise the remainder of the exhaust gas. This equation determines the exhaust burned gas mass fraction.
The equations use these variables.
Engine exhaust temperature | |
Exhaust manifold inlet-specific enthalpy | |
Exhaust gas specific heat | |
Intake port air mass flow rate | |
Fuel mass flow rate | |
Exhaust mass flow rate | |
Intake fuel mass fraction | |
| yexh,i | Exhaust mass fraction for i = CO2, CO, HC, NOx, air, burned gas, and PM |
Exhaust mass flow rate for i = CO2, CO, HC, NOx, air, burned gas, and PM | |
| Tbrake | Engine brake torque |
| N | Engine speed |
| yexh,air | Exhaust air mass fraction |
| yexh,b | Exhaust air burned mass fraction |
Power Accounting
For the power accounting, the block implements equations that depend on Torque model.
When you set Torque model to Simple Torque Lookup, the block implements these equations.
| Bus Signal | Description | Equations | ||
|---|---|---|---|---|
|
|
| Intake heat flow | |
PwrExhHeatFlw | Exhaust heat flow | |||
PwrCrkshft | Crankshaft power | |||
| PwrFuel | Fuel input power | ||
PwrLoss | All losses | |||
| Not used | |||
When you set Torque model to Torque Structure, the block implements these equations.
| Bus Signal | Description | Equations | ||
|---|---|---|---|---|
|
|
| Intake heat flow | |
PwrExhHeatFlw | Exhaust heat flow | |||
PwrCrkshft | Crankshaft power | |||
| PwrFuel | Fuel input power | ||
PwrFricLoss | Friction loss | |||
PwrPumpLoss | Pumping loss | |||
PwrHeatTrnsfrLoss | Heat transfer loss | |||
| Not used | |||
| hexh | Exhaust manifold inlet-specific enthalpy |
| hintk | Intake port specific enthalpy |
Intake port air mass flow rate | |
Fuel mass flow rate | |
Exhaust mass flow rate | |
| ω | Engine speed |
| Tbrake | Brake torque |
| Tpump | Engine pumping work offset to inner torque |
| Tfric | Engine friction torque |
| LHV | Fuel lower heating value |
Examples
Ports
Input
Output
Parameters
References
[1] Heywood, John B. Internal Combustion Engine Fundamentals. New York: McGraw-Hill, 1988.
Extended Capabilities
Version History
Introduced in R2017a