Hauptinhalt
Results for
Have you ever learned that something you were doing manually in MATLAB was already possible using a built-in feature? Have you ever written a function only to later realize (or be told) that a built-in function already did what you needed?
Two such moments come to mind for me.
1. Did you realize that you can set conditional breakpoints? Neither did I, until someone showed me that feature. To do that, open or create a file in the editor, right click on a line number for any line that contains code, and select Set Conditional Breakpoint... This will bring up a dialog wherein you can type any logical condition for which execution should be paused. Before I learned about this, I would manually insert if-statements during debugging. Then, after fixing each bug, I would have to delete those statements. This built-in feature is so much better.
2. Have you ever needed to plot horizontal or vertical lines in a plot? For the longest time, I would manually code such lines. Then, I learned about xline() and yline(). Not only is less code required, these lines automatically span the entire axes while zooming, panning, or adjusting axis limits!
Share your own Aha! moments below. This will help everyone learn about MATLAB functionality that may not be obvious or front and center.
(Note: While File Exchange contains many great contributions, the intent of this thread is to focus on built-in MATLAB functionality.)
The carot symbol on my keyboard (ˆ shift+6) doesn't work on matlab. Matlab doesn't recognize it so I can't write any equation with power symbol. I tried every possible solution on the web and it doesn't work. even in the character viewer I don't have any result when I search ''caret".
Exciting news for students! 🚀Simulink Student Challenge 2023 is live! Unleash your engineering skills and compete for exciting rewards. Submission deadline is December 12th, 2023!
Over the weekend I came across a pi approximation using durations of years and weeks (image below, Wolfram, eq. 89), accurate to 6 digits using the average Gregorian year (365.2425 days).
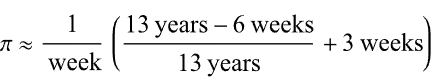
Here it is in MATLAB. I divided by 1 week at the end rather than multiplying by its reciprocal because you can’t divide a numeric by a duration in MATLAB (1/week).
weeks = @(n)n*days(7);
piApprox = ((years(13)-weeks(6))/years(13) + weeks(3)) / weeks(1)
% piApprox = 3.141593493469302
Here’s a breakdown
- The first argument becomes 12.885 yrs / 13 yrs or 0.99115
- Add three weeks: 0.99115 + 3 weeks = 21.991 days
- The reduced fraction becomes 21.991 days / 7 days
Now it looks a lot closer to the more familiar approximation for pi 22/7 but with greater precision!
I'm in a community conference in Boston today and see what snacks we get! The organizer said it's a coincidence, but it's definitly a good idea to have them in our MathWorks community meetings.
(Sorry - it should be 2023b by now.)
spy
I'm curious how the community uses the hold command when creating charts and graphics in MATLAB. In short, hold on sets up the axes to add new objects to the axes while hold off sets up the axes to reset when new objects are added.
When you use hold on do you always follow up with hold off? What's your reasoning on this decision?
Can't wait to discuss this here! I'd love to hear from newbies and experts alike!
Calling all students! New to MATLAB or need helpful resources? Check out our MATLAB GitHub for Students repository! Find MATLAB examples, videos, cheat sheets, and more!
Visit the repository here: MATLAB GitHub for Students
Imagine x is a large vector and you want the smallest 10 elements. How might you do it?
The way we've solved ODEs in MATLAB has been relatively unchanged at the user-level for decades. Indeed, I consider ode45 to be as iconic as backslash! There have been a few new solvers in recent years -- ode78 and ode89 for example -- and various things have gotten much faster but if you learned how to solve ODEs in MATLAB in 1997 then your knowledge is still applicable today.
In R2023b, there's a completely new framework for solving ODEs and I love it! You might argue that I'm contractually obliged to love it since I'm a MathWorker but I can assure you this is the real thing!
I wrote it up in a tutorial style on The MATLAB Blog https://blogs.mathworks.com/matlab/2023/10/03/the-new-solution-framework-for-ordinary-differential-equations-odes-in-matlab-r2023b/
The new interface makes a lot of things a much easier to do. Its also setting us up for a future where we'll be able to do some very cool algorithmic stuff behind the scenes.
Let me know what you think of the new functionality and what you think MathWorks should be doing next in the area of ODEs.
To solve the puzzle, first unscramble each of the words on the left. Then rearrange the letters in the yellow shaded boxes to complete the sentence on the right.
If you enjoyed this puzzle let me know with a like or in the comments below and I'll post more of them. Please don't post your answer, or any hints, and spoil it for those who come across this puzzle after you!! If you want to check your answer, you can messge me your guess through the link on my profile card (click on my name, Rena Berman, above and then on the envelope icon in the top right corner of the profile card that appears).
The MATLAB Answers community is an invaluable resource for all MATLAB users, providing selfless assistance and support. However, with the emergence of AI-based chatbots, like chatGPT, there may be concerns about the future relevance and utility of the MATLAB Answer community. What are your thoughts?
I've now seen linear programming questions pop up on Answers recently, with some common failure modes for linprog that people seem not to understand.
One basic failure mode is an infeasible problem. What does this mean, and can it be resolved?
The most common failure mode seems to be a unbounded problem. What does this mean? How can it be avoided/solved/fixed? Is there some direction I can move where the objective obviously grows without bounds towards +/- inf?
Finally, I also see questions where someone wants the tool to produce all possible solutions.
A truly good exposition about linear programming would probably result in a complete course on the subject, and Aswers is limited in how much I can write (plus I'll only have a finite amount of energy to keep writing.) I'll try to answer each sub-question as separate answers, but if someone else would like to offer their own take, feel free to do so as an answer, since it has been many years for me since I learned linear programming.
Introduction
Comma-separated lists are really very simple. You use them all the time. Here is one:
a,b,c,d
That is a comma-separated list containing four variables, the variables a, b, c, and d. Every time you write a list separated by commas then you are writing a comma-separated list. Most commonly you would write a comma-separated list as inputs when calling a function:
fun(a,b,c,d)
or as arguments to the concatenation operator or cell construction operator:
[a,b,c,d]
{a,b,c,d}
or as function outputs:
[a,b,c,d] = fun();
It is very important to understand that in general a comma-separated list is NOT one variable (but it could be). However, sometimes it is useful to create a comma-separated list from one variable (or define one variable from a comma-separated list), and MATLAB has several ways of doing this from various container array types:
struct_array.field % all elements
struct_array(idx).field % selected elements
cell_array{:} % all elements
cell_array{idx} % selected elements
string_array{:} % all elements
string_array{idx} % selected elements
Note that in all cases, the comma-separated list consists of the content of the container array, not subsets (or "slices") of the container array itself (use parentheses to "slice" any array). In other words, they will be equivalent to writing this comma-separated list of the container array content:
content1, content2, content3, .. , contentN
and will return as many content arrays as the original container array has elements (or that you select using indexing, in the requested order). A comma-separated list of one element is just one array, but in general there can be any number of separate arrays in the comma-separated list (zero, one, two, three, four, or more). Here is an example showing that a comma-separated list generated from the content of a cell array is the same as a comma-separated list written explicitly:
>> C = {1,0,Inf};
>> C{:}
ans =
1
ans =
0
ans =
Inf
>> 1,0,Inf
ans =
1
ans =
0
ans =
Inf
How to Use Comma-Separated Lists
Function Inputs: Remember that every time you call a function with multiple input arguments you are using a comma-separated list:
fun(a,b,c,d)
and this is exactly why they are useful: because you can specify the arguments for a function or operator without knowing anything about the arguments (even how many there are). Using the example cell array from above:
>> vertcat(C{:})
ans =
1
0
Inf
which, as we should know by now, is exactly equivalent to writing the same comma-separated list directly into the function call:
>> vertcat(1,0,Inf)
ans =
1
0
Inf
How can we use this? Commonly these are used to generate vectors of values from a structure or cell array, e.g. to concatenate the filenames which are in the output structure of dir:
S = dir(..);
F = {S.name}
which is simply equivalent to
F = {S(1).name, S(2).name, S(3).name, .. , S(end).name}
Or, consider a function with multiple optional input arguments:
opt = {'HeaderLines',2, 'Delimiter',',', 'CollectOutputs',true);
fid = fopen(..);
C = textscan(fid,'%f%f',opt{:});
fclose(fid);
Note how we can pass the optional arguments as a comma-separated list. Remember how a comma-separated list is equivalent to writing var1,var2,var3,..., then the above example is really just this:
C = textscan(fid,'%f%f', 'HeaderLines',2, 'Delimiter',',', 'CollectOutputs',true)
with the added advantage that we can specify all of the optional arguments elsewhere and handle them as one cell array (e.g. as a function input, or at the top of the file). Or we could select which options we want simply by using indexing on that cell array. Note that varargin and varargout can also be useful here.
Function Outputs: In much the same way that the input arguments can be specified, so can an arbitrary number of output arguments. This is commonly used for functions which return a variable number of output arguments, specifically ind2sub and gradient and ndgrid. For example we can easily get all outputs of ndgrid, for any number of inputs (in this example three inputs and three outputs, determined by the number of elements in the cell array):
C = {1:3,4:7,8:9};
[C{:}] = ndgrid(C{:});
which is thus equivalent to:
[C{1},C{2},C{3}] = ndgrid(C{1},C{2},C{3});
Further Topics:
MATLAB documentation:
Click on these links to jump to relevant comments below:
Dynamic Indexing (indexing into arrays with arbitrary numbers of dimensions)
Summary
Just remember that in general a comma-separated list is not one variable (although they can be), and that they are exactly what they say: a list (of arrays) separated with commas. You use them all the time without even realizing it, every time you write this:
fun(a,b,c,d)
Similar to what has happened with the wishlist threads (#1 #2 #3 #4 #5), the "what frustrates you about MATLAB" thread has become very large. This makes navigation difficult and increases page load times.
So here is the follow-up page.
What should you post where?
Next Gen threads (#1): features that would break compatibility with previous versions, but would be nice to have
@anyone posting a new thread when the last one gets too large (about 50 answers seems a reasonable limit per thread), please update this list in all last threads. (if you don't have editing privileges, just post a comment asking someone to do the edit)
After reading Rik's comment I looked for a list of Matlab releases and their corresponding features. Wiki: Matlab contains an exhaustive list, but what about having a lean version directly in the forum?
If this is useful, feel free to expand the list and to insert additions. Thank you.
There are multiple ways to create a graphical user interface (GUI) in Matlab. Which method is the best depends on multiple factors: the complexity of the project, to what extent it should be a long-term solution, on what releases your GUI should work, your available time, your skill level, and probably other factors I'm forgetting.
To keep the thread clear I'll attempt to provide a short outline a few ways in this question, and leave the details for the answers. (@anyone with editing privileges: feel free to update the section below if I missed something important and am slow in editing this question)
---------------------------------------------------------------------------------------------------
GUIDE
GUIDE is probably the first tool new users will encounter. It is very useful for quickly putting something together, but it is otherwise fairly limited. It requires maintaining (and distributing) both a .m and a .fig file. Note that the GUIDE environment will be removed in a future release. After GUIDE is removed, existing GUIDE apps will continue to run in Matlab but they will not be editable in GUIDE. If you're starting a new GUI, don't use GUIDE. If you're updating an existing GUIDE GUI, migrate it to AppDesigner. In R2021a the first step for this removal was taken: all templates except the blank template have been removed.
GUILT
Although I haven't had a detailed look myself, it seems a list like this is not complete without at least mentioning the GUI Layout Toolbox, which is available on the file exchange and offers a lot of customization options.
Programmatic GUIs
You can bypass GUIDE and use the normal figures and functions like uicontrol to build GUIs from code. This makes the design less visual, but more flexible for future additions.
App Designer
The official successor to GUIDE, AppDesigner is not based on functions, but works similar to a class. It uses uifigure and mostly uses graphical elements that are incompatible with 'normal' GUIs that are created with a figure (or .fig).
Sie können auch eine Website aus der folgenden Liste auswählen:
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom(English)
Asien-Pazifik
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)