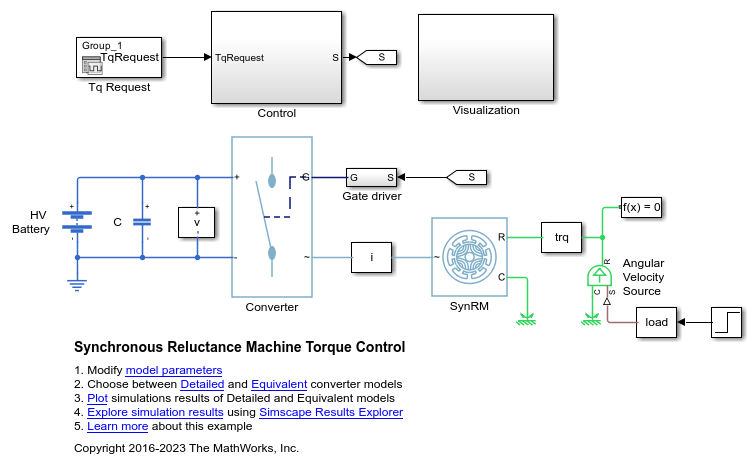
Synchronous Reluctance Machine
Synchronous reluctance machine with sinusoidal flux distribution
Libraries:
Simscape /
Electrical /
Electromechanical /
Reluctance & Stepper
Description
The Synchronous Reluctance Machine block represents a synchronous reluctance machine (SynRM) with sinusoidal flux distribution. The figure shows the equivalent electrical circuit for the stator windings.
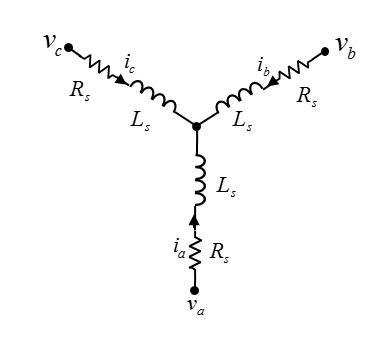
You can also model the stator windings either in a delta-wound or in an open-end
configuration by setting Winding type to
Delta-wound or Open-end,
respectively.
Motor Construction
The diagram shows the motor construction with a single pole-pair on the rotor. For the axes convention shown, when rotor mechanical angle θr is zero, the a-phase and permanent magnet fluxes are aligned. The block supports a second rotor axis definition for which rotor mechanical angle is defined as the angle between the a-phase magnetic axis and the rotor q-axis.

Equations
The combined voltage across the stator windings is
where:
va, vb, and vc are the individual phase voltages across the stator windings.
Rs is the equivalent resistance of each stator winding.
ia, ib, and ic are the currents flowing in the stator windings.
ψa, ψb, and ψc are the magnetic fluxes that link each stator winding.
The permanent magnet, excitation winding, and the three stator windings contribute to the flux that links each winding. The total flux is defined as
where:
Laa, Lbb, and Lcc are the self-inductances of the stator windings.
Lab, Lac, Lba, Lbc, Lca, and Lcb are the mutual inductances of the stator windings.
and
where:
θr is the rotor mechanical angle.
θe is the rotor electrical angle.
rotor offset is
0if you define the rotor electrical angle with respect to the d-axis, or-pi/2if you define the rotor electrical angle with respect to the q-axis.Ls is the stator self-inductance per phase. This value is the average self-inductance of each of the stator windings.
Lm is the stator inductance fluctuation. This value is the amplitude of the fluctuation in self-inductance and mutual inductance with changing rotor angle.
Ms is the stator mutual inductance. This value is the average mutual inductance between the stator windings.
Simplified Equations
Applying the Park transformation to the block electrical defining equations produces an expression for torque that is independent of rotor angle.
The Park transformation, P, is defined as
where θe is the electrical angle. The electrical angle depends on the rotor mechanical angle and the number of pole pairs such that
where:
N is the number of pole pairs.
θr is the rotor mechanical angle.
Applying the Park transformation to the first two electrical defining equations produces equations that define the behavior of the block:
where:
id, iq, and i0 are the d-axis, q-axis, and zero-sequence currents, defined by
where ia, ib, and ic are the stator currents.
vd, vq, and v0 are the d-axis, q-axis, and zero-sequence currents, defined by
where va, vb, and vc are the stator currents.
The dq0 inductances are defined, respectively as
.
Rs is the stator resistance per phase.
N is the number of rotor pole pairs.
T is the rotor torque. For the Synchronous Reluctance Machine block, torque flows from the machine case (block conserving port C) to the machine rotor (block conserving port R).
TL is the load torque.
Bm is the rotor damping.
ω is the rotor mechanical rotational speed.
J is the rotor inertia.
Calculating Iron Losses
To calculate iron losses in the Synchronous Reluctance Machine block, choose whether you want to model them by specifying magnetizing resistance, parameterize them based on the Steinmetz equation, or if you want to tabulate the losses as a function of currents and rotor speed.
If you set the Stator parameterization parameter to
Specify Ls, Lm, and Ms or Specify Ld,
Lq, and L0 and Modeling fidelity to
Constant Ld and Lq, then specify the
Magnetizing resistance parameter to model iron
losses.
In the Iron Losses settings, if you set the
Model parameter to Specify tabulated Steinmetz
coefficients or Tabulate with current and
speed, the iron losses are applied to the mechanical side as a
reduction in the electrical torque:
where wmin is minimum
rotor speed to start taking iron losses into account, and it is equal to
1
rad/s.
The total power dissipated is equal to the sum of the iron losses and the copper losses:
To model the iron losses based on the Steinmetz equation, set the
Stator parameterization parameter to
Specify Ld, Lq, and L0 and the Modeling
fidelity parameter to Tabulated Ld and
Lq. The Steinmetz method scales for different motor speeds or
electrical frequencies so that iron loss data is only required as function of
motor currents.
If, in the Iron losses settings, you set the
Model parameter to Specify tabulated
Steinmetz coefficients, the iron losses are given by:
where:
khr(id,iq) is the Rotor hysteresis loss coefficient, k_hr(id,iq).
kJr(id,iq) is the Rotor eddy current loss coefficient, k_Jr(id,iq).
ker(id,idq) is the Rotor excess current loss coefficient, k_er(id,iq).
khs(id,iq) is the Stator hysteresis loss coefficient, k_hs(id,iq).
kJs(id,iq) is the Stator eddy current loss coefficient, k_Js(id,iq).
kes(id,iq) is the Stator excess current loss coefficient, k_es(id,iq).
is the electrical frequency, in Hz.
To model the iron losses by tabulating them independently for rotor and
stator, set the Stator parameterization parameter to
Specify Ld, Lq, and L0 and the Modeling
fidelity parameter to Tabulated Ld and
Lq.
Then, if in the Iron losses settings, you set the
Model parameter to Tabulate with current
and speed, the iron losses are given by:
where w is the Rotor speed vector, w parameter.
If you expose the thermal ports of the block, the power dissipated in each phase act as heat sources in the stator and in the rotor:
If you specify the magnetizing resistance, the iron loss in the rotor is equal to a percentage of the total iron losses. This percentage remains constant and does not depend on other states:
Then the remaining iron loss is distributed among the different stator phases:
Model Thermal Effects
You can expose thermal ports to model the effects of losses that convert power to heat. To expose the thermal ports, set the Modeling option parameter to either:
No thermal port— The block does not contain thermal ports.Show thermal port— The block contains multiple thermal conserving ports.
For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. You can specify nominal values using different sources, including the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
Examples
Assumptions
The flux distribution is sinusoidal.
Ports
Conserving
Parameters
References
[1] Kundur, P. Power System Stability and Control. New York, NY: McGraw Hill, 1993.
[2] Anderson, P. M. Analysis of Faulted Power Systems. Hoboken, NJ: Wiley-IEEE Press, 1995.
[3] Moghaddam, R. Synchronous Reluctance Machine (SynRM) in Variable Speed Drives (VSD) Applications - Theoretical and Experimental Reevaluation. KTH School of Electrical Engineering, Stockholm, Sweden, 2011.