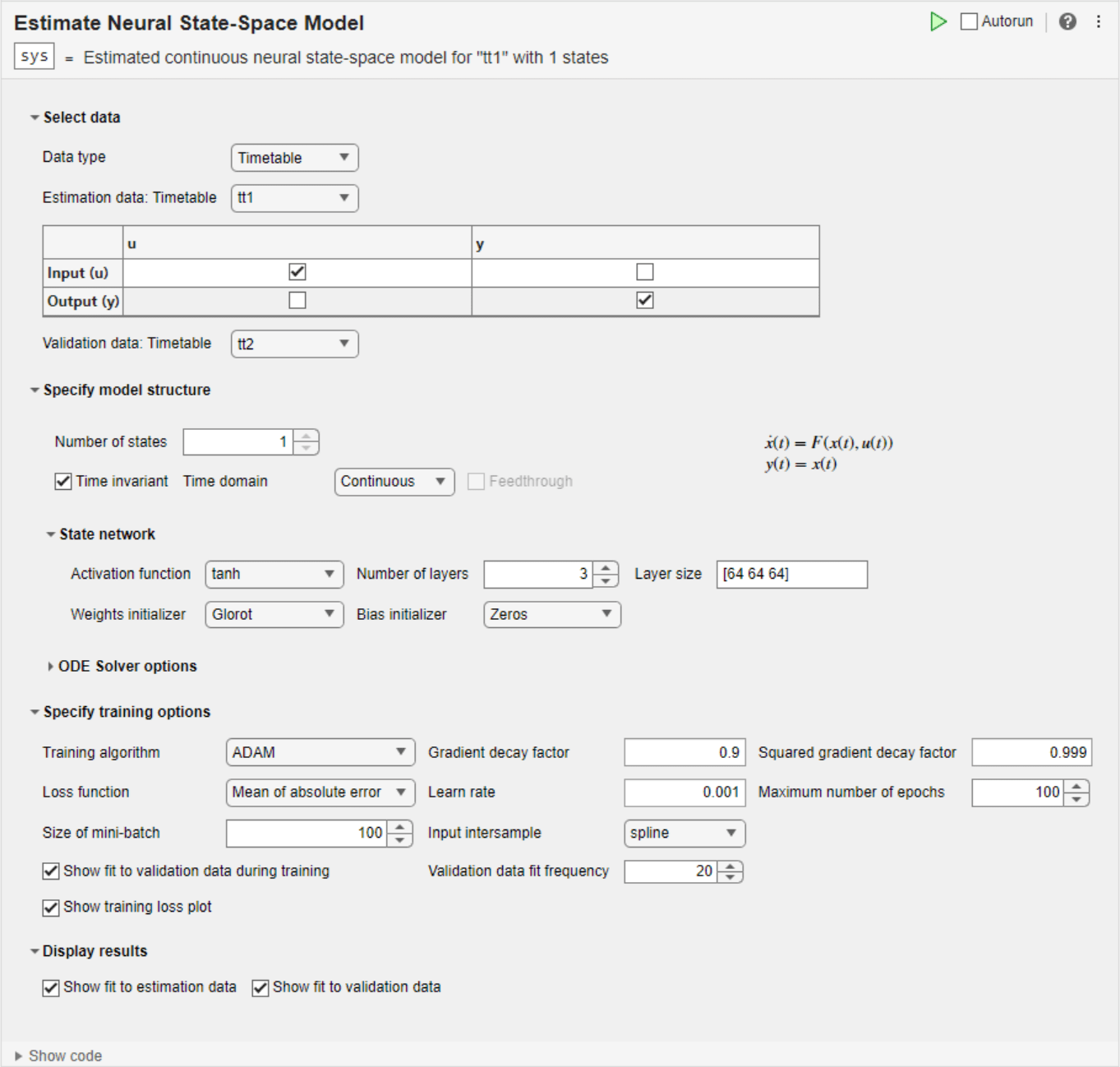
Estimate Neural State-Space Model

Estimate neural state-space model in the Live Editor

Since R2023b

Description

The Estimate Neural State-Space Model task lets you interactively estimate and validate a neural state-space model, using time-domain data. You can define and vary the structure and the parameters of the networks and the solver. The task automatically generates MATLAB^® code for your live script. For more information about Live Editor tasks, see Add Interactive Tasks to a Live Script. For more information about state-space estimation, see What Are State-Space Models?

The Estimate Neural State-Space Model task is independent of the more general System Identification app. Use the System Identification app when you want to compute and compare estimates for multiple model structures.

To get started, load experiment data that contains input and output data into your MATLAB workspace and then import that data into the task. Then specify a model structure to estimate. The task gives you controls and plots that help you experiment with different model parameters and compare how well the output of each model fits the measurements.

More

Related Functions

The code that Estimate Neural State-Space Model generates uses the following functions and objects.

• createMLPNetwork

• nssTrainingOptions

• nlssest

The task estimates an idNeuralStateSpace state-space model.

×

Open the Task

To add the Estimate Neural State-Space Model task to a live script in the MATLAB Editor:

• On the Live Editor tab, select Task > Estimate Neural State-Space Model.

• In a code block in your script, type a relevant keyword, such as neuralstatespace or nlssest. Select Estimate State-Space Model from the suggested command completions.

Examples

Estimate Neural State-Space Model with Live Editor Task

Use the Estimate Neural State-Space Model Live Editor Task to estimate a neural state-space model and compare the model output with the measurement data.

Open this example to see a preconfigured script containing the task.

Generate Data

For this example, generate data by simulating a first-order linear system. First, fix the random generator seed to guarantee reproducibility.

rng(0)

Create a first-order discrete dynamical system in tf form with one input and one output, convert it to discrete time using a sample time of 0.1 sec, and use ss to obtain a state-space realization.

Ts = 0.1;
sys = ss(c2d(tf(1,[1 1]),Ts));

The identification of a neural state-space system requires you to have measurement of the system states. Therefore, transform the state-space coordinates so that the output is equal to the state. Alternatively you can augment the output equation to include the state among the measured signals.

sys.b = sys.b*sys.c;
sys.c = 1;

In general, it is good practice to use multiple experiments, each containing a different trajectory, as doing so is more likely to yield a better coverage of the state-input space. Furthermore, using long trajectories tends to reduce both the accuracy and efficiency of the estimation. However, for this example, use a single trajectory for estimation.

Define a time vector and a random input sequence for estimation (training).

te = 0:Ts:10; 
ue = randn(length(te),size(sys.B,2));

Generate an output response to the random input sequence by simulating the system from a zero initial condition. The first (vertical) dimension in ye must be time and the second (horizontal) dimension must be the specific output in the output vector signal.

ye = lsim(sys,ue,te,zeros(size(sys.B,1),1));

Define a shorter time vector and a random input sequence for validation.

tv = 0:Ts:1;
uv = randn(length(tv),size(sys.B,2));

Generate an output response to the random input sequence by simulating the system, from a zero initial condition.

yv = lsim(sys,uv,tv,zeros(size(sys.B,1),1));

Import Data into the Task

In the Select data section, set Data Type to Numeric, Sample Time to 0.01, Estimation Data: Input (u) to ue, Estimation Data: Output (y) to ye, Validation Data: Input (u) to uv, and Validation Data: Output (y) to yv.

Specify Model Structure and State Network

In the Specify model structure section, set the Number of states to 1 and select the discrete-time domain. In the State network section, set the Number of layers to 1 and specify Layer size as 16. Leave the other options unchanged.

Note that since for this example the output is equal to the state, there is no Output network section. Since the latent dimension is not specified, there are no Encoder network and Decoder network sections.

Examine Training and Display Options

In the Specify training options section, the Training algorithm is set to ADAM, with a Learn rate of 0.001. The number of epochs is set to 100, and so is the mini-batch size. For more information on these options, see nssTrainingOptions.

In the Display results section, both the Show fit to estimation data and (since you have specified validation data) the Show fit to validation data are selected.

Execute Live Task

Execute the task from the Live Editor tab using Run. During training, a plot displays the training losses of the state and output networks.

Generating estimation report...done.

After training, two plots displays the model fit on the estimation and validation data.

Generate Code

To display the code that the task generates, click (Show code) at the bottom of the parameter section. The code that you see reflects the current parameter configuration of the task.

Related Examples

• What are Neural State-Space Models?
• Estimate Neural State-Space System
• Neural State-Space Model of SI Engine Torque Dynamics
• Neural State-Space Model of Simple Pendulum System

Parameters

Select data

Data type — Data type for input and output data

Numeric (default) | Timetable | iddata object

The task accepts numeric measurement values that are uniformly sampled in time. Input and output signals can contain multiple channels. Data can be packaged as numeric arrays, in an iddata object, or in a timetable object. For multiexperiment data, numeric and timetable data can be packaged as cell arrays. For cell arrays of timetables, all timetables must contain the same variable names. Data objects handle multiexperiment data internally.

The data type you choose determines whether you must specify additional parameters.

• Numeric — Specify Sample Time and Start Time in the time unit that you select. Additionally, you need to specify different workspace variables containing the input and output signals to be used for estimation and (if available) validation.

• Timetable — Specify no additional parameters because the timetable already contains the input and output signals and sampling information.

• iddata object — Specify no additional parameters because the iddata object already contains the input and output signals and sampling information.

Sample time — Sample time

1 (default) | positive scalar

Sample time at which estimation and (if available) validation data are collected, specified as a positive scalar, in the unit specified by the following time unit drop down list. You can specify a sample time only when Data Type is Numeric.

Time unit — Time unit

seconds (default) | minutes | milliseconds | ...

Time unit for the Sample time and Start time parameters. You can specify one of the following units:

• nanoseconds

• microseconds

• milliseconds

• seconds

• minutes

• hours

• days

• weeks

• months

• years

You can specify a sample time only when Data Type is Numeric.

Start time — Start time

0 (default) | nonnegative scalar

Start time for the estimation and (if available) validation data, specified as a nonnegative scalar, in the unit specified by the preceding time unit drop down list. This value is relevant only if you deselect the Time invariant checkbox. You can specify a start time only when Data Type is Numeric.

Estimation data: Input (u) — Name of the input data variable used for estimation

valid variable name

Name of the input data variable used for estimation, selected from the MATLAB workspace choices. Use this parameter, along with Estimation data: Output (y), when Data Type is Numeric.

Estimation data: Output (y) — Name of the output data variable used for estimation

valid variable name

Name of the output data variable used for estimation, selected from the MATLAB workspace choices. Use this parameter, along with Estimation data: Input (u), when Data Type is Numeric.

Estimation data: Timetable — Variable name of timetable object containing input and output data for estimation

valid variable name

Select the timetable object variable name from the MATLAB workspace choices. If you use a use a cell arrays of timetables, all timetables must contain the same variable names. Use this parameter when Data type is Timetable.

Estimation data: Object — Variable name of data object containing input and output data for estimation

valid variable name

Select the iddata object variable name from the MATLAB workspace choices. Use this parameter when Data type is iddata object.

Validation data: Input (u) — Name of the input data variable used for validation

valid variable name

Name of the input data variable used for validation, selected from the MATLAB workspace choices. Use this parameter, along with Validation data: Output (y), when Data Type is Numeric.

Validation data: Output (y) — Name of the output data variable used for validation

valid variable name

Name of the output data variable used for validation, selected from the MATLAB workspace choices. Use this parameter, along with Validation data: Input (y), when Data Type is Numeric.

Validation data: Timetable — Variable name of timetable object containing input and output data for validation

valid variable name

Select the timetable object variable name from the MATLAB workspace choices. The timetables containing the validation data must have the same variable names as the ones in the timetables selected for estimation in Estimation data: Timetable. Use this parameter when Data type is Timetable. Specifying validation data is optional but recommended.

Validation data: Object — Variable name of data object containing input and output data for validation

valid variable name

Select the iddata object variable name from the MATLAB workspace choices. Use this parameter when Data type is iddata object. Specifying validation data is optional but recommended.

Specify model structure

Number of states — Number of states

number of outputs (default) | positive integer

Number of states in the model to estimate. It must be less than or equal to the number of outputs in the data. For more information, see idNeuralStateSpace.

Latent dimension — Dimension of internal state

finite positive integer

Dimension of the internal (latent) state. When this option is left blank (default), there is no encoder or decoder in the model. To add an encoder or decoder to your model, specify this option as a finite positive integer. For more information, see the LatentDim property of idNeuralStateSpace.

Time invariant — Estimate a time invariant model

on (default) | off

Deselect this option to estimate a model in which the state equation explicitly depends on time, other than states and inputs. When this option is left selected (default), the state equation depends explicitly only on the current state and input vectors. For more information, see the isTimeInvariant property of idNeuralStateSpace.

Time domain — Continuous or discrete time domain

Continuous (default) | Discrete

Select a continuous-time or discrete-time model.

Feedthrough — Estimate a model with direct feedthrough

off (default) | on

Select this option to estimate a model in which the output equation explicitly depends on the input vector. When this option is left unselected (default), the output equation does not depend explicitly on the input vector. For more information, see the HasFeedthrough property of idNeuralStateSpace.

State network

Activation function — Type of activation function for all hidden layers

tanh (default) | sigmoid | relu | leakyRelu | clippedRelu | elu | gelu | swish | softplus | scaling | softmax | none

You can specify one of the following as the activation function for all hidden layers of the state network: tanh, sigmoid, relu, leakyRelu, clippedRelu, elu, gelu, swish, softplus, scaling, or softmax. All of these are available in Deep Learning Toolbox™. softplus and scaling also require Reinforcement Learning Toolbox™.

Also, you can now choose to not use an activation function by specifying the activation function as none.

For more information, see createMLPNetwork.

Number of layers — Number of hidden layers

2 (default) | nonnegative integer

Number of hidden layers of the state network, specified as a nonnegative integer. It must be equal to the number of elements of the vector you specify in Layer size in the State network section. If you specify 0, the state network has no hidden layer, and therefore expresses a linear function.

Layer size — Size of the hidden layers

[64 64] (default) | vector of positive integers

Size of the hidden layers for the state network, specified as a vector of positive integers. Each number specifies the number of neurons (network nodes) for each hidden layer (each layer is fully-connected). For example, [10 20 8] specifies a network with three hidden layers, the first (after the network input) having 10 neurons, the second having 20 neurons, and the last (before the network output), having 8 neurons. Note that the output layer is also fully-connected, and you cannot change its size.

The number of elements in Layer size must be equal to the value specified in Number of layers in the State network section.

Weights initializer — Weights initializer method

glorot (default) | he | orthogonal | narrow-normal | zeros | ones

Weights initializer method for all the hidden layers of the state network. You can specify one of the following:

• glorot — uses the Glorot method (default).

• he — uses the He method.

• orthogonal — uses the orthogonal method.

• narrow-normal — uses the narrow-normal method.

• zeros — initializes all weights to zero.

• ones — initializes all weights to one.

Bias initializer — Bias initializer method

zeros (default) | ones | narrow-normal

Bias initializer method for all the hidden layers of the state network. You can specify one of the following:

• zeros — initializes all biases to zero (default).

• ones — initializes all biases to one.

• narrow-normal — uses the narrow-normal method.

Output network

Activation function — Type of activation function for all hidden layers

tanh (default) | sigmoid | relu | leakyRelu | clippedRelu | elu | gelu | swish | softplus | scaling | softmax | none

You can specify one of the following as the activation function for all hidden layers of the output network: tanh, sigmoid, relu, leakyRelu, clippedRelu, elu, gelu, swish, softplus, scaling, or softmax. Of these, softplus and scaling require Reinforcement Learning Toolbox.

Also, you can now choose to not use an activation function by specifying the activation function as none.

For more information, see createMLPNetwork.

Number of layers — Number of hidden layers

2 (default) | nonnegative integer

Number of hidden layers of the output network, specified as a nonnegative integer. It must be equal to the number of elements of the vector you specify in Layer size in the Output network section. If you specify 0, the output network has no hidden layer, and therefore expresses a linear function.

Layer size — Size of the hidden layers

[64 64] (default) | vector of positive integers

Size of the hidden layers for the output network, specified as a vector of positive integers. Each number specifies the number of neurons (network nodes) for each hidden layer (each layer is fully-connected). For example, [10 20 8] specifies a network with three hidden layers, the first (after the network input) having 10 neurons, the second having 20 neurons, and the last (before the network output), having 8 neurons. Note that the output layer is also fully-connected, and you cannot change its size.

The number of elements Layer size must be equal to the value specified in Number of layers in the Output network section.

Weights initializer — Weights initializer method

glorot (default) | he | orthogonal | narrow-normal | zeros | ones

Weights initializer method for all the hidden layers of the output network. You can specify one of the following:

• glorot — uses the Glorot method (default).

• he — uses the He method.

• orthogonal — uses the orthogonal method.

• narrow-normal — uses the narrow-normal method.

• zeros — initializes all weights to zero.

• ones — initializes all weights to one.

Bias initializer — Bias initializer method

zeros (default) | ones | narrow-normal

Bias initializer method for all the hidden layers of the output network. You can specify one of the following:

• zeros — initializes all biases to zero (default).

• ones — initializes all biases to one.

• narrow-normal — uses the narrow-normal method.

Encoder network

Activation function — Type of activation function for all hidden layers

tanh (default) | sigmoid | relu | leakyRelu | clippedRelu | elu | gelu | swish | softplus | scaling | softmax | none

You can specify one of the following as the activation function for all hidden layers of the encoder network: tanh, sigmoid, relu, leakyRelu, clippedRelu, elu, gelu, swish, softplus, scaling, or softmax. All of these are available in Deep Learning Toolbox. softplus and scaling also require Reinforcement Learning Toolbox.

Also, you can now choose to not use an activation function by specifying the activation function as none.

For more information, see createMLPNetwork.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

Number of layers — Number of hidden layers

2 (default) | nonnegative integer

Number of hidden layers of the encoder network, specified as a nonnegative integer. It must be equal to the number of elements of the vector you specify in Layer size in the Encoder network section. If you specify 0, the encoder network has no hidden layer, and therefore expresses a linear function.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

Layer size — Size of the hidden layers

[64 64] (default) | vector of positive integers

Size of the hidden layers for the encoder network, specified as a vector of positive integers. Each number specifies the number of neurons (network nodes) for each hidden layer (each layer is fully-connected). For example, [10 20 8] specifies a network with three hidden layers, the first (after the network input) having 10 neurons, the second having 20 neurons, and the last (before the network output), having 8 neurons. Note that the output layer is also fully-connected, and you cannot change its size.

The number of elements in Layer size must be equal to the value specified in Number of layers in the Encoder network section.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

Weights initializer — Weights initializer method

glorot (default) | he | orthogonal | narrow-normal | zeros | ones

Weights initializer method for all the hidden layers of the encoder network. You can specify one of the following:

• glorot — uses the Glorot method (default).

• he — uses the He method.

• orthogonal — uses the orthogonal method.

• narrow-normal — uses the narrow-normal method.

• zeros — initializes all weights to zero.

• ones — initializes all weights to one.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

Bias initializer — Bias initializer method

zeros (default) | ones | narrow-normal

Bias initializer method for all the hidden layers of the encoder network. You can specify one of the following:

• zeros — initializes all biases to zero (default).

• ones — initializes all biases to one.

• narrow-normal — uses the narrow-normal method.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

Decoder network

Activation function — Type of activation function for all hidden layers

tanh (default) | sigmoid | relu | leakyRelu | clippedRelu | elu | gelu | swish | softplus | scaling | softmax | none

You can specify one of the following as the activation function for all hidden layers of the decoder network: tanh, sigmoid, relu, leakyRelu, clippedRelu, elu, gelu, swish, softplus, scaling, or softmax. All of these are available in Deep Learning Toolbox. softplus and scaling also require Reinforcement Learning Toolbox.

Also, you can now choose to not use an activation function by specifying the activation function as none.

For more information, see createMLPNetwork.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

Number of layers — Number of hidden layers

2 (default) | nonnegative integer

Number of hidden layers of the decoder network, specified as a nonnegative integer. It must be equal to the number of elements of the vector you specify in Layer size in the Decoder network section. If you specify 0, the decoder network has no hidden layer, and therefore expresses a linear function.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

Layer size — Size of the hidden layers

[64 64] (default) | vector of positive integers

Size of the hidden layers for the decoder network, specified as a vector of positive integers. Each number specifies the number of neurons (network nodes) for each hidden layer (each layer is fully-connected). For example, [10 20 8] specifies a network with three hidden layers, the first (after the network input) having 10 neurons, the second having 20 neurons, and the last (before the network output), having 8 neurons. Note that the output layer is also fully-connected, and you cannot change its size.

The number of elements in Layer size must be equal to the value specified in Number of layers in the Decoder network section.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

Weights initializer — Weights initializer method

glorot (default) | he | orthogonal | narrow-normal | zeros | ones

Weights initializer method for all the hidden layers of the decoder network. You can specify one of the following:

• glorot — uses the Glorot method (default).

• he — uses the He method.

• orthogonal — uses the orthogonal method.

• narrow-normal — uses the narrow-normal method.

• zeros — initializes all weights to zero.

• ones — initializes all weights to one.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

Bias initializer — Bias initializer method

zeros (default) | ones | narrow-normal

Bias initializer method for all the hidden layers of the decoder network. You can specify one of the following:

• zeros — initializes all biases to zero (default).

• ones — initializes all biases to one.

• narrow-normal — uses the narrow-normal method.

Dependencies

To enable this parameter, specify the Latent dimension parameter as a finite positive integer.

ODE Solver options

Input step size — Initial step size

Auto (default) | positive scalar

Initial step size used to simulate the model (when continuous-time). It is specified as either Auto or a positive scalar. If you specify Auto, then the solver bases the initial step size on the slope of the solution at the initial time point.

For more information, see odeset.

Maximum step size — Maximum step size

Auto (default) | positive scalar

Maximum step size used to simulate the model (when continuous-time). It is an upper bound on the size of any step taken by the solver, and it is specified as either Auto or a positive scalar. If you specify Auto, then the value used is one-tenth of the difference between final and initial time.

For more information, see odeset.

Absolute tolerance — Absolute tolerance

0.01 (default) | positive scalar

Absolute tolerance used to simulate continuous time models, specified as a positive scalar. It is the largest allowable absolute error. That is, when the solution approaches 0, AbsoluteTolerance is the threshold below which you do not worry about the accuracy of the solution since it is effectively 0.

For more information, see odeset.

Relative tolerance — Relative tolerance

0.01 (default) | positive scalar

Relative tolerance used to simulate the continuous time models, specified as a positive scalar. This tolerance measures the error relative to the magnitude of each solution component. That is, it controls the number of significant digits in a solution (except when is smaller than the absolute tolerance).

For more information, see odeset.

Specify training options

Training algorithm — Training algorithm used to train the networks

ADAM (default) | SGDM | RMSProp | LBFGS

You can specify one of the following:

• ADAM — uses the Adam (adaptive moment estimation) algorithm.

• SGDM — uses the SGDM (stochastic gradient descent with momentum) algorithm.

• RMSProp — uses the RMSProp (root mean square propagation) algorithm.

• LBFGS — uses the L-BFGS (limited-memory BFGS) algorithm.

For more information on these algorithms, see the Algorithms section of trainingOptions (Deep Learning Toolbox).

Gradient decay factor — Decay rate of gradient moving average

0.9 (default) | nonnegative scalar less than 1

Decay rate of gradient moving average for the Adam solver, specified as a nonnegative scalar less than 1. The gradient decay rate is denoted by β1 in the Adaptive Moment Estimation (Deep Learning Toolbox) section.

The default value works well for most tasks. You can specify a Gradient decay factor only when Training algorithm is ADAM.

For more information, see Adaptive Moment Estimation (Deep Learning Toolbox).

Squared gradient decay factor — Decay rate of squared gradient moving average

nonnegative scalar less than 1

Decay rate of squared gradient moving average for the RMSProp solver, specified as a nonnegative scalar less than 1. The default value is 0.999 for the Adam solver and 0.9 for the RMSProp solver.

Typical values of the decay rate are 0.9, 0.99, and 0.999, corresponding to averaging lengths of 10, 100, and 1000 parameter updates, respectively.

You can specify a Squared gradient decay factor only when Training algorithm is ADAM or RMSProp.

For more information, see Root Mean Square Propagation (Deep Learning Toolbox).

Momentum — Contribution of previous step

0.95 (default) | nonnegative scalar less than 1

Contribution of the parameter update step of the previous iteration to the current iteration of stochastic gradient descent with momentum, specified as a scalar from 0 to 1.

A value of 0 means no contribution from the previous step, whereas a value of 1 means maximal contribution from the previous step. The default value works well for most tasks.

You can specify Momentum only when Training algorithm is SGDM.

For more information, see Stochastic Gradient Descent with Momentum (Deep Learning Toolbox).

Beta — Coefficient applied to tune the reconstruction loss of an autoencoder

0 (default) | nonnegative scalar

Coefficient applied to tune the reconstruction loss of an autoencoder, specified as a nonnegative scalar.

Reconstruction loss measures the difference between the original input (x) and its reconstruction (xr) after encoding and decoding. You calculate this loss as the L2 norm of (x - xr) divided by the batch size (N).

Dependencies

To enable this option, specify the Latent dimension parameter as a finite positive integer.

Lambda — Loss function regularization constant

0 (default) | positive scalar

Constant coefficient applied to the regularization term added to the loss function, specified as a positive scalar.

The loss function with the regularization term is given by:

${\widehat{V}}_N\left(\theta \right)=\frac{1}{N}{\displaystyle \sum _{t=1}^N{\epsilon }^2\left(t,\theta \right)+ \frac{1}{N}\lambda {\Vert \theta \Vert }^2}$

where t is the time variable, N is the size of the batch, ε is the sum of the reconstruction loss and autoencoder loss, θ is a concatenated vector of weights and biases of the neural network, and λ is the regularization constant that you can tune.

For more information, see Regularized Estimates of Model Parameters.

Loss function — Type of function used to calculate loss

Mean of absolute error (default) | Mean of squared error

You can specify one of the following:

• Mean of absolute error — uses the mean value of the absolute error.

• Mean of squared error — uses the mean value of the squared error.

Maximum iterations — Maximum number of iterations

100 (default) | positive integer

Maximum number of iterations to use for training, specified as a positive integer.

The L-BFGS solver is a full-batch solver, which means that it processes the entire training set in a single iteration.

You can specify Maximum iterations only when Training algorithm is LBFGS.

Line search method — Method to find suitable learning rate

"weak-wolfe" (default) | "strong-wolfe" | "backtracking"

Method to find suitable learning rate, specified as one of these values:

• "weak-wolfe" — Search for a learning rate that satisfies the weak Wolfe conditions. This method maintains a positive definite approximation of the inverse Hessian matrix.

• "strong-wolfe" — Search for a learning rate that satisfies the strong Wolfe conditions. This method maintains a positive definite approximation of the inverse Hessian matrix.

• "backtracking" — Search for a learning rate that satisfies sufficient decrease conditions. This method does not maintain a positive definite approximation of the inverse Hessian matrix.

You can specify Line search method only when Training algorithm is LBFGS.

History size — Number of state updates to store

10 (default) | positive integer

Number of state updates to store, specified as a positive integer. Values between 3 and 20 suit most tasks.

The L-BFGS algorithm uses a history of gradient calculations to approximate the Hessian matrix recursively. For more information, see Limited-Memory BFGS (Deep Learning Toolbox).

You can specify History size only when Training algorithm is LBFGS.

Initial inverse Hessian factor — Initial value that characterizes approximate inverse Hessian matrix

1 (default) | positive scalar

Initial value that characterizes the approximate inverse Hessian matrix, specified as a positive scalar.

To save memory, the L-BFGS algorithm does not store and invert the dense Hessian matrix B. Instead, the algorithm uses the approximation $$B_{k-m}^{-1}\approx {\lambda }_{k}I$$, where m is the history size, the inverse Hessian factor $${\lambda }_k$$ is a scalar, and I is the identity matrix. The algorithm then stores the scalar inverse Hessian factor only. The algorithm updates the inverse Hessian factor at each step.

The initial inverse hessian factor is the value of $${\lambda }_0$$.

For more information, see Limited-Memory BFGS (Deep Learning Toolbox).

You can specify Initial inverse Hessian factor only when Training algorithm is LBFGS.

Maximum line search iterations — Maximum number of line search iterations

20 (default) | positive integer

Maximum number of line search iterations to determine the learning rate, specified as a positive integer.

You can specify Maximum line search iterations only when Training algorithm is LBFGS.

Learn rate — Learning rate used for training

positive scalar

Learning rate used for training, specified as a positive scalar. The default value is 0.001 for Adam and RMSProp solvers and 0.01 for SGDM solver.

If the learning rate is too small, then training can take a long time. If the learning rate is too large, then training might reach a suboptimal result or diverge. You can specify Learn rate only when Training algorithm is ADAM, SGDM, or RMSProp.

Maximum number of epochs — Maximum number of epochs

100 (default) | positive integer

Maximum number of epochs to use for training, specified as a positive integer. An epoch is the full pass of the training algorithm over the entire training set. You can specify Maximum number of epochs only when Training algorithm is ADAM, SGDM, or RMSProp.

Size of mini-batch — Validation period

1000 (default) | positive integer

Size of the mini-batch to use for each training iteration, specified as a positive integer. A mini-batch is a subset of the training set that is used to evaluate the gradient of the loss function and update the weights.

If the mini-batch size does not evenly divide the number of training samples, then the estimation process discards the training data that does not fit into the final complete mini-batch of each epoch. You can specify Size of mini-batch only when Training algorithm is ADAM, SGDM, or RMSProp.

Window size — Size of data frames

10000 (default) | positive integer

Number of samples in each frame or batch when segmenting data for model training, specified as a positive integer.

Overlap — Size of overlap

0 (default) | integer

Number of samples in the overlap between successive frames when segmenting data for model training, specified as an integer. A negative integer indicates that certain data samples are skipped when creating the data frames.

Input intersample — Input interpolation method

foh (default) | zoh | spline | cubic | makima | pchip

You can select one of the following options:

• zoh — Zero-order hold interpolation method

• foh — First-order hold interpolation method

• cubic — Cubic interpolation method

• makima — Modified Akima interpolation method

• pchip — Shape-preserving piecewise cubic interpolation method

• spline — Spline interpolation method (default)

This is the interpolation method used to interpolate the input when integrating continuous-time neural state-space models. For more information, see interpolation methods in interp1.

Show fit to validation data during training — Enable plot showing comparison of predicted and measured estimation outputs

on (default) | off

Enable displaying a validation plot periodically during training. The validation plot shows a comparison between the predicted output response to measured validation inputs and the measured validation outputs. The plot also displays the model fit percentage.

Validation data fit frequency — Validation period

20 (default) | positive integer

This is the number of epochs after which the validation plot is updated with a new comparison (new predicted output against measured outputs). For example, if Validation data fit frequency is 10, the validation plot is updated every 10 epochs. For more information, see nlssest.

Show training loss plot — Show training loss plot

on (default) | off

Enable displaying a training plot during training (estimation). The training plot shows how the state and output network loss values evolve after each training epoch.

Display results

Show fit to estimation data — Enable plot showing comparison of predicted and measured estimation outputs

on (default) | off

After estimation (training), plot a comparison between the predicted output response to measured estimation inputs and the measured estimation outputs. Selecting this parameter also displays the model fit percentage.

Show fit to validation data — Enable plot showing comparison of predicted and measured validation outputs

on (default) | off

After estimation (training), plot a comparison between the predicted output response to measured validation inputs and the measured validation outputs. Selecting this parameter also displays the model fit percentage. This parameter is available only if you select validation data in the Select Data section.

Version History

Introduced in R2023b

R2024b: Multi-experiment data support

The Estimate Neural State-Space Model Live Editor task now supports multi-experiment data.