Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

Identifizieren linearer Modelle mithilfe der App „System Identification“

Einführung

Ziele

Schätzen und Validieren linearer Modelle aus SISO-Daten, um herauszufinden, welches Modell die Systemdynamiken am besten beschreibt.

Nach Abschluss dieses Tutorials können Sie die folgenden Aufgaben mithilfe der App „System Identification“ ausführen:

• Importieren von Datenarrays aus dem MATLAB^®-Arbeitsbereich in die App.

• Plotten der Daten.

• Verarbeiten von Daten durch Entfernen von Offsets aus den Eingangs- und Ausgangssignalen.

• Schätzen, Validieren und Vergleichen linearer Modelle.

• Exportieren von Modellen in den MATLAB-Arbeitsbereich.

Hinweis

In diesem Tutorial wird am Beispiel von Zeitdomänendaten veranschaulicht, wie Sie lineare Modelle schätzen können. Derselbe Workflow kann auch zum Anpassen von Frequenzdomänendaten verwendet werden.

Dieses Tutorial basiert auf dem Beispiel in Abschnitt 17.3 der Publikation System Identification: Theory for the User, 2. Auflage, von Lennart Ljung, Prentice Hall PTR, 1999.

Datenbeschreibung

In diesem Tutorial wird die Datendatei dryer2.mat verwendet, die Single-Input/Single-Output-(SISO-)Zeitdomänendaten von einem Eingang und einem Ausgang aus dem Feedback Process Trainer PT326 enthält. Die Eingangs- und Ausgangssignale umfassen jeweils 1000 Datenstichproben.

Dieses System erwärmt die Luft am Einlass mithilfe eines Heizdrahtgeflechts, ähnlich wie bei einem Haartrockner. Der Eingang ist die Stromversorgung der Heizdrähte und der Ausgang ist die Lufttemperatur am Auslass.

Vorbereiten von Daten für System Identification

Laden von Daten in den MATLAB-Arbeitsbereich

Laden Sie die Daten in der Datei dryer2.mat, indem Sie den folgenden Befehl in das MATLAB-Befehlsfenster eingeben:

load dryer2

Mit diesem Befehl werden die Daten als zwei Spaltenvektoren, u2 bzw. y2, in den MATLAB-Arbeitsbereich geladen. Die Variable u2 steht für die Eingangsdaten und y2 für die Ausgangsdaten.

Öffnen der App „System Identification“

Geben Sie zum Öffnen der App „System Identification“ den folgenden Befehl in das MATLAB-Befehlsfenster ein:

systemIdentification

In der Titelleiste wird der Standard-Sitzungsname, Untitled, angezeigt.

Importieren von Datenarrays in die App „System Identification“

Sie können die Single-Input/Single-Output-(SISO-)Daten im MATLAB-Arbeitsbereich aus einer Beispieldatendatei dryer2.mat in die App importieren.

Sie müssen die Beispieldaten bereits in MATLAB geladen haben, wie in Laden von Daten in den MATLAB-Arbeitsbereich beschrieben, und die App „System Identification“ geöffnet haben, wie in Öffnen der App „System Identification“ beschrieben.

Falls Sie diese Schritte noch ausführen müssen, klicken Sie hier.

So importieren Sie Datenarrays in die App „System Identification“:

1. Wählen Sie Import data > Time domain data aus. Dadurch wird das Dialogfenster „Import Data“ (Daten importieren) geöffnet.

   

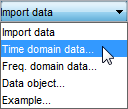
2. Geben Sie im Dialogfenster „Import Data“ folgende Optionen an:

   • Input: Geben Sie u2 als Namen der Eingangsgröße ein.

   • Output: Geben Sie y2 als Namen der Ausgangsgröße ein.

   • Data name: Ändern Sie den Standardnamen in data. Dieser Name wird nach Abschluss des Importvorgangs für die Daten in der App „System Identification“ angezeigt.

   • Starting time: Geben Sie 0 als Anfangszeit ein. Dieser Wert wird als Anfangswert der Zeitachse in Zeitdiagrammen angezeigt.

   • Sample Time: Geben Sie 0.08 als Zeit zwischen aufeinanderfolgenden Abtastungen in Sekunden an. Dieser Wert ist in dem Versuch die tatsächliche Abtastzeit.

   Das Dialogfenster „Import Data“ sieht nun in etwa wie folgt aus:

   

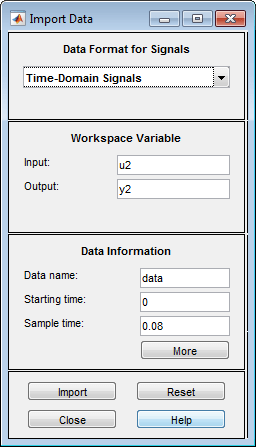
3. Klicken Sie im Bereich Data Information auf More, um das Dialogfenster zu erweitern, und geben Sie die folgenden Optionen an:

   Input Properties

   • Intersample: Übernehmen Sie den Standardwert zoh (Zero-Order Hold, Haltefunktion nullter Ordnung), um anzugeben, dass das Eingangssignal während der Datenerfassung zwischen den Abtastungen stückweise konstant war. Diese Einstellung gibt das Verhalten der Eingangssignale zwischen Abtastungen an, wenn Sie die resultierenden Modelle zwischen zeitdiskreten und zeitkontinuierlichen Darstellungen transformieren.

   • Period: Übernehmen Sie den Standardwert inf, um einen nichtperiodischen Eingang anzugeben.

     Hinweis

     Für einen periodischen Eingang geben Sie die Gesamtzahl der Perioden des Eingangssignals in Ihrem Versuch an.

   Channel Names

   • Input: Geben Sie power ein.

     Tipp

     Durch die Benennung von Kanälen können Sie Daten in Diagrammen leichter identifizieren. Für multivariable Eingangs- und Ausgangssignale können Sie die Namen einzelner Eingangs-(Input-) und Ausgangs-(Output-)kanäle angeben und Kommas als Trennzeichen verwenden.

   • Output: Geben Sie temperature ein.

   Physical Units of Variables

   • Input: Geben Sie W als Einheit für die Leistung ein.

     Tipp

     Wenn mehrere Eingänge und Ausgänge vorhanden sind, geben Sie die Input- und Output-Einheiten, die den jeweiligen Kanälen entsprechen, in einer Liste mit Kommas als Trennzeichen ein.

   • Output: Geben Sie ^oC als Einheit für die Temperatur ein.

   Notes: Geben Sie Kommentare zum Versuch oder zu den Daten ein. Beispielsweise können Sie den Namen und das Datum des Versuchs sowie eine Beschreibung der Versuchsbedingungen eingeben. Wenn Sie Modelle aus diesen Daten schätzen, werden Ihre Hinweise von diesen Modellen übernommen.

   Das erweiterte Dialogfenster „Import Data“ sieht nun in etwa wie folgt aus:

   

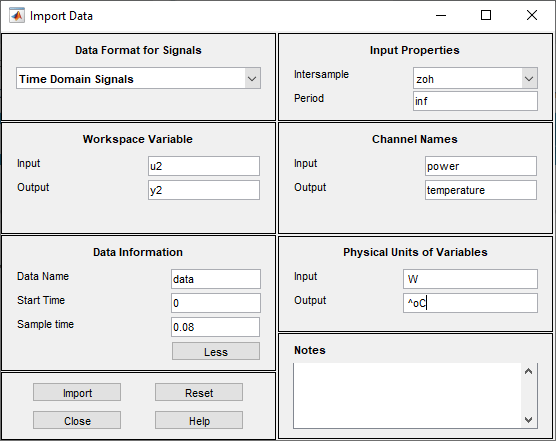
4. Klicken Sie auf Import, um die Daten zur App „System Identification“ hinzuzufügen. In der App wird ein Symbol zur Darstellung der Daten angezeigt.

   

5. Klicken Sie auf Close, um das Dialogfenster „Import Data“ zu schließen.

Plotten und Verarbeiten der Daten

In diesem Teil des Tutorials werten Sie die Daten aus und verarbeiten sie für die Systemidentifikation. Sie erfahren, wie Sie folgende Aufgaben ausführen:

• Plotten der Daten.

• Entfernen von Offsets aus den Daten, indem die Mittelwerte vom Eingang und Ausgang subtrahiert werden.

• Splitten der Daten in zwei Teile, um einen Teil für die Modellschätzung und den anderen Teil für die Modellvalidierung zu verwenden.

Sie subtrahieren die Mittelwerte von den jeweiligen Signalen, weil Sie in der Regel lineare Modelle erstellen, die die Antworten für Abweichungen von einem physikalischen Gleichgewicht beschreiben. Bei stationären Daten kann man davon ausgehen, dass die mittleren Pegel der Signale einem solchen Gleichgewicht entsprechen. Auf diese Weise können Sie Modelle um den Nullwert herum suchen, ohne die absoluten Gleichgewichtspegel in physikalischen Einheiten modellieren zu müssen.

Sie müssen die importierten Daten bereits in die App „System Identification“ importiert haben, wie in Importieren von Datenarrays in die App „System Identification“ beschrieben.

Falls Sie diesen Schritt noch ausführen müssen, klicken Sie hier.

So können Sie die Daten plotten und verarbeiten:

1. Aktivieren Sie das Kontrollkästchen Time plot, um das Zeitdiagramm zu öffnen. Wenn das Diagrammfenster leer ist, klicken Sie in der App „System Identification“ auf das Symbol data.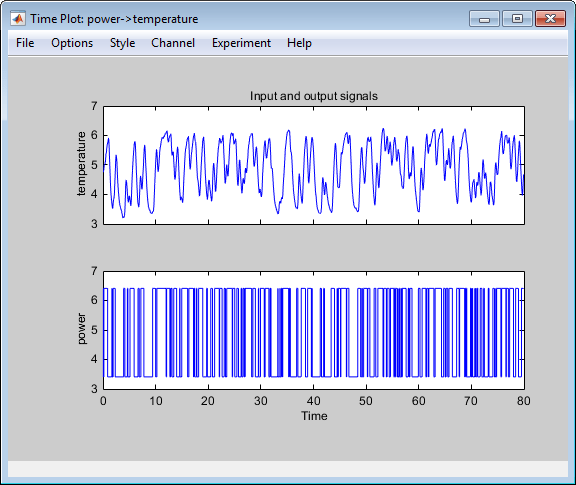

   

   Entlang der oberen Achsen sind die Ausgangsdaten (Temperatur) und entlang der unteren Achsen die Eingangsdaten (Leistung) abgebildet. Sowohl die Eingangs- als auch die Ausgangsdaten weisen Mittelwerte ungleich null auf.

2. Subtrahieren Sie den mittleren Eingangswert von den Eingangsdaten und den mittleren Ausgangswert von den Ausgangsdaten. Wählen Sie in der App „System Identification“ die Optionen <--Preprocess > Remove means (Vorverarbeitung > Mittelwerte entfernen) aus.

   

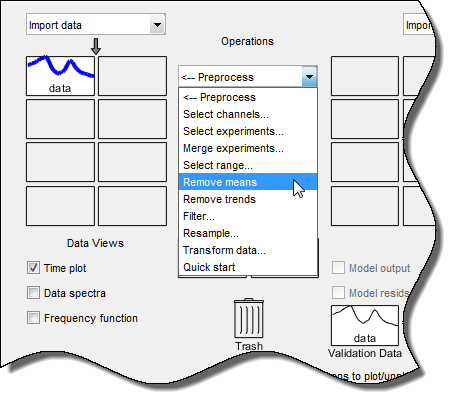
   Auf diese Weise wird der App „System Identification“ ein neuer Datensatz mit dem Standardnamen datad (das Suffix d steht für detrend, Trendbereinigung) hinzugefügt und das Fenster mit dem Zeitdiagramm wird aktualisiert, sodass sowohl die ursprünglichen Daten als auch die trendbereinigten Daten angezeigt werden. Die trendbereinigten Daten haben einen Mittelwert von null.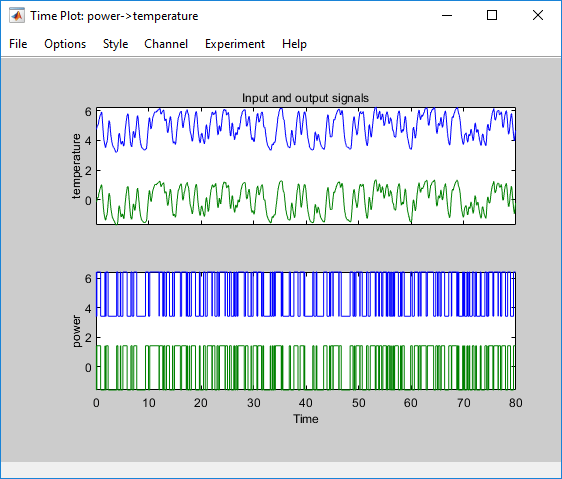

   

3. Geben Sie die trendbereinigten Daten an, die zum Schätzen von Modellen verwendet werden sollen. Ziehen Sie den Datensatz datad auf das Rechteck Working Data (Arbeitsdaten).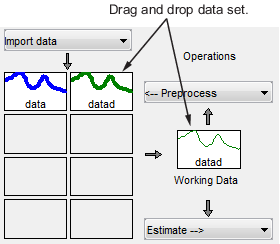

   

   Klicken Sie alternativ mit der rechten Maustaste auf das Symbol datad, um das Dialogfenster „Data/model Info“ zu öffnen.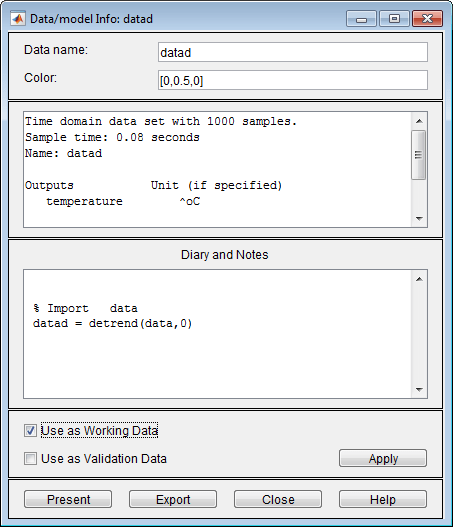

   

   Aktivieren Sie das Kontrollkästchen Use as Working Data (Als Arbeitsdaten verwenden). Klicken Sie auf Apply und anschließend auf Close. Auf diese Weise wird datad dem Rechteck Working Data hinzugefügt.

4. Splitten Sie die Daten in zwei Teile und geben Sie den ersten Teil für die Modellschätzung und den zweiten Teil für die Modellvalidierung an.

   1. Wählen Sie <--Preprocess > Select range (Vorverarbeitung > Bereich auswählen) aus, um das Fenster „Select Range“ zu öffnen.

      

   2. Erstellen Sie im Fenster „Select Range“ einen Datensatz, der die ersten 500 Stichproben enthält. Geben Sie im Feld Samples die Zahl 1 500 ein.

      Tipp

      Sie können Datenstichproben auch mithilfe der Maus auswählen, indem Sie klicken und ein Rechteck um einen Bereich im Diagramm ziehen. Wenn Sie Abtastungen entlang der Eingangskanal-Achsen auswählen, wird auch der entsprechende Bereich entlang der Ausgangskanal-Achsen ausgewählt.

   3. Geben Sie in das Feld Data name den Namen data_est ein.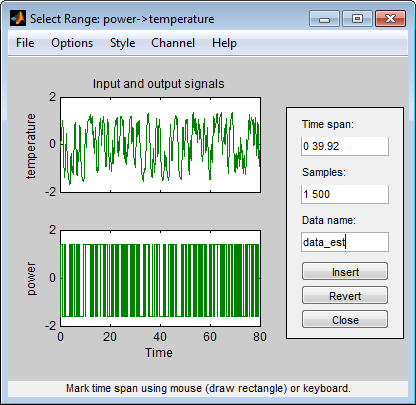

      

   4. Klicken Sie auf Insert, um diesen neuen Datensatz zur App „System Identification“ hinzuzufügen, damit er für die Modellschätzung verwendet werden kann.

   5. Wiederholen Sie diesen Prozess, um einen zweiten Datensatz zu erstellen, der eine Teilmenge der Daten enthält, die für die Validierung verwendet werden soll. Geben Sie im Fenster „Select Range“ die letzten 500 Stichproben in das Feld Samples ein. Geben Sie den Namen data_val in das Feld Data name ein. Klicken Sie auf Insert, um diesen neuen Datensatz zur App „System Identification“ hinzuzufügen.

      

   6. Klicken Sie auf Close, um das Fenster „Select Range“ zu schließen.

5. Ziehen Sie in der App „System Identification“ data_est per Drag and Drop auf das Rechteck Working Data (Arbeitsdaten) und data_val auf das Rechteck Validation Data (Validierungsdaten).

   

6. Zum Abrufen von Informationen zu einem Datensatz klicken Sie mit der rechten Maustaste auf dessen Symbol. Klicken Sie beispielsweise mit der rechten Maustaste auf data_est, um das Dialogfenster „Data/model Info“ zu öffnen.

   

   Sie können auch bestimmte Werte im Dialogfenster „Data/model Info“ ändern. Beispiele:

   • Sie können den Namen des Datensatzes im Feld Data name ändern.

   • Sie können die Farbe des Datensymbols im Feld Color ändern. Sie geben Farben mithilfe von RGB-Werten an (relative Werte für Rot, Grün und Blau). Jeder Wert liegt zwischen 0 und 1. Beispielsweise bedeutet [1,0,0], dass nur Rot vorhanden ist und weder Grün noch Blau in die Gesamtfarbe gemischt werden.

   • Sie können Befehle, die für diesen Datensatz ausgeführt werden, im Bereich Diary and Notes anzeigen oder bearbeiten. Dieser Bereich enthält das Befehlszeilenäquivalent zu der von Ihnen in der App „System Identification“ ausgeführten Verarbeitung. Wie beispielsweise im Dialogfenster „Data/model Info: estimate“ dargestellt, ergibt sich der Datensatz data_est aus dem Importieren der Daten, der Trendbereinigung der Mittelwerte und dem Auswählen der ersten 500 Datenstichproben.

      % Import   data          
      datad = detrend(data,0)  
      data_est = datad([1:500])

     Ausführliche Informationen zu diesen und zu weiteren Befehlen der Toolbox finden Sie auf den entsprechenden Referenzseiten.

Im Dialogfenster „Data/model Info“ werden auch die Gesamtzahl der Stichproben, die Abtastzeit und die Namen sowie Einheiten der Ausgangs- und Eingangskanäle angezeigt. Diese Informationen sind nicht editierbar.

Tipp

Alternativ können Sie in der App „System Identification“ einfach Preprocess > Quick start auswählen, um alle Datenverarbeitungsschritte in diesem Tutorial auszuführen.

Weitere Informationen.  Ausführliche Informationen zu unterstützten Datenverarbeitungsoperationen, z. B. erneutes Abtasten oder Filtern der Daten, finden Sie unter Preprocess Data.

Speichern der Sitzung

Nach der Verarbeitung der Daten, wie in Plotten und Verarbeiten der Daten beschrieben, können Sie im Dialogfenster beliebige Datensätze löschen, die Sie für die Schätzung und Validierung nicht benötigen, und Ihre Sitzung speichern. Sie können diese Sitzung später öffnen und sie als Ausgangspunkt für die Modellschätzung und -validierung verwenden, ohne diese vorbereitenden Schritte wiederholen zu müssen.

Sie müssen die Daten bereits in der App „System Identification“ verarbeitet haben, wie in Plotten und Verarbeiten der Daten beschrieben.

So können Sie bestimmte Datensätze aus einer Sitzung löschen und die Sitzung speichern:

1. In der App „System Identification“:

   1. Verschieben Sie den Datensatz data per Drag and Drop nach Trash (Papierkorb).

   2. Verschieben Sie den Datensatz datad per Drag and Drop nach Trash.

   Alternativ können Sie durch Drücken der Taste Delete (Entf) auf Ihrer Tastatur die Datensätze nach Trash verschieben.

   Hinweis

   Nach Trash verschobene Elemente werden nicht gelöscht. Wenn Sie Elemente dauerhaft löschen möchten, wählen Sie Options > Empty trash (Optionen > Papierkorb leeren) aus.

   Die folgende Abbildung zeigt die App „System Identification“ nach dem Verschieben von Elementen nach Trash.

   

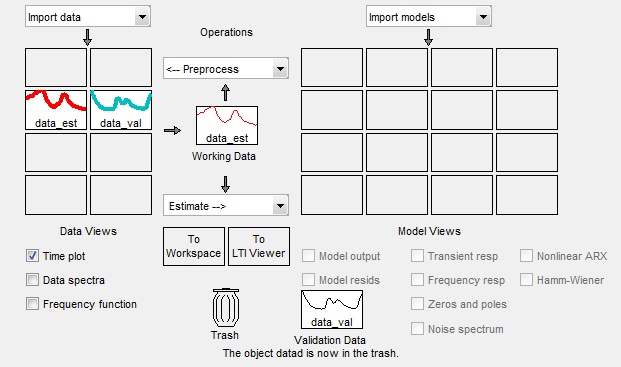
2. Verschieben Sie die Datensätze data_est und data_val per Drag and Drop, um die leeren Rechtecke auszufüllen, wie in der folgenden Abbildung dargestellt.

   

3. Wählen Sie File > Save session as (Datei > Sitzung speichern unter) aus, um das Dialogfenster „Save Session“ (Sitzung speichern) zu öffnen, und wechseln Sie in den Ordner, in dem Sie die Sitzungsdatei speichern möchten.

4. Geben Sie in das Feld File name den Namen der Sitzung dryer2_processed_data ein und klicken Sie auf Save. Die resultierende Datei hat die Dateinamenerweiterung .sid.

Tipp

Sie können eine gespeicherte Sitzung beim Starten der App „System Identification“ öffnen, indem Sie den folgenden Befehl in die MATLAB-Eingabeaufforderung eingeben:

systemIdentification('dryer2_processed_data')

Weitere Informationen zum Verwalten von Sitzungen finden Sie unter Starting and Managing Sessions.

Schätzung linearer Modelle mithilfe von „Quick Start“

So schätzen Sie lineare Modelle mithilfe von „Quick Start“

Sie können lineare Modelle mithilfe der Funktion „Quick Start“ in der App „System Identification“ schätzen. Mit „Quick Start“ werden möglicherweise die endgültigen linearen Modelle erstellt, die Sie verwenden möchten, oder Sie erhalten die erforderlichen Informationen zum Konfigurieren der Schätzung exakter parametrischer Modelle, z. B. Zeitkonstanten, Eingangsverzögerungen und Resonanzfrequenzen.

Sie müssen die Daten für die Schätzung bereits verarbeitet haben, wie in Plotten und Verarbeiten der Daten beschrieben.

Falls Sie diesen Schritt noch ausführen müssen, klicken Sie hier.

Wählen Sie in der App „System Identification“ die Optionen Estimate > Quick start (Schätzen > Schnellstart) aus.

Auf diese Weise werden Sprungantwort- und Frequenzgangdiagramme sowie Diagramme mit dem Ausgang von Zustandsraum- und Polynommodellen generiert. Weitere Informationen zu diesen Diagrammen finden Sie unter Validierung des mit „Quick Start“ erstellten Modells.

Typen von mit „Quick Start“ erstellten linearen Modellen

„Quick Start“ schätzt die vier folgenden Modelltypen und fügt der App „System Identification“ Folgendes mit den Standardnamen hinzu:

• imp: Sprungantwort über einen Zeitraum mithilfe des Algorithmus impulseest.

• spad: Frequenzantwort über eine Reihe von Frequenzen mithilfe des Algorithmus spa. Der Frequenzgang ist die Fourier-Transformation der Impulsantwort eines linearen Systems.

  Standardmäßig wird das Modell an 128 Frequenzwerten ausgewertet, die von 0 bis zur Nyquist-Frequenz reichen.

• arxqs: Autoregressives (ARX) Modell vierter Ordnung mithilfe des Algorithmus arx.

  Dieses Modell ist parametrisch und hat folgende Struktur:

  $$\begin{array}{l}y(t)+a_{1}y(t-1)+\dots +a_{na}y(t-n_a)=\\ {\text{ b}}_{\text{1}}u(t-n_k)+\dots +b_{nb}u(t-n_k-n_b+1)+e(t)\end{array}$$

  y(t) steht dabei für den Ausgang zum Zeitpunkt t, u(t) steht für den Eingang zum Zeitpunkt t, n_a ist die Anzahl der Polstellen, n_b ist die Anzahl der b-Parameter (gleich der Anzahl der Nullstellen plus 1), n_k ist die Anzahl der Abtastungen, bevor sich der Eingang auf den Ausgang des Systems auswirkt (die sogenannte Verzögerung oder Totzeit des Modells), und e(t) ist die Störung durch weißes Rauschen. Die Software System Identification Toolbox™ schätzt die Parameter $$a_1\dots a_n$$ und $$b_1\dots b_n$$ mithilfe der Eingangs- und Ausgangsdaten des Schätzdatensatzes.

  In arxqs, werden n_a=n_b=4 und n_k anhand des Sprungantwortmodells imp geschätzt.

• n4s3: Zustandsraummodell, das mithilfe von n4sid berechnet wurde. Der Algorithmus wählt die Modellordnung (in diesem Fall 3) automatisch aus.

  Dieses Modell ist parametrisch und hat folgende Struktur:

  $$\begin{array}{l}\frac{dx}{dt}=Ax(t)+Bu(t)+Ke(t)\\ y(t)=Cx(t)+Du(t)+e(t)\end{array}$$

  y(t) steht dabei für den Ausgang zum Zeitpunkt t, u(t) steht für den Eingang zum Zeitpunkt t, x ist der Zustandsvektor und e(t) ist die Störung durch weißes Rauschen. Das Produkt System Identification Toolbox schätzt die Zustandsraummatrizen A, B, C, D und K.

Hinweis

Mit der Option „Quick Start“ wird kein Transferfunktionsmodell oder Prozessmodell erstellt, die jedoch auch gute Ausgangsmodelltypen sein können.

Validierung des mit „Quick Start“ erstellten Modells

„Quick Start“ generiert während der Modellschätzung die folgenden Diagramme, um Sie bei der Validierung der Qualität der Modelle zu unterstützen:

• Sprungantwortdiagramm

• Frequenzgangdiagramm

• Modellausgangsdiagramm

Um diese Diagramme erstellen zu können, müssen Sie bereits Modelle mit „Quick Start“ geschätzt haben, wie in So schätzen Sie lineare Modelle mithilfe von „Quick Start“ beschrieben.

Falls Sie diesen Schritt noch ausführen müssen, klicken Sie hier.

Sprungantwortdiagramm.  Das folgende Sprungantwortdiagramm zeigt Übereinstimmungen zwischen den verschiedenen Modellstrukturen und den gemessenen Daten, was bedeutet, dass alle diese Strukturen ähnliche Dynamiken aufweisen.

Tipp

Wenn Sie das Diagrammfenster geschlossen haben, aktivieren Sie das Kontrollkästchen Transient resp, um dieses Fenster erneut zu öffnen. Wenn das Diagramm leer ist, klicken Sie im Fenster der App „System Identification“ auf die Modellsymbole, um die Modelle im Diagramm anzuzeigen.

Sprungantwort für imp, arxqs und n4s3

Tipp

Sie können das Sprungantwortdiagramm verwenden, um die Totzeit linearer Systeme zu schätzen. Beispielsweise zeigt das vorherige Sprungantwortdiagramm eine Zeitverzögerung von etwa 0,25 s an, bevor das System auf den Eingang reagiert. Diese Antwortverzögerung, oder Totzeit, entspricht in etwa drei Abtastungen, da die Abtastzeit für diesen Datensatz 0.08 s beträgt.

Frequenzgangdiagramm.  Das folgende Frequenzgangdiagramm zeigt Übereinstimmungen zwischen den verschiedenen Modellstrukturen und den gemessenen Daten, was bedeutet, dass alle diese Strukturen ähnliche Dynamiken aufweisen.

Tipp

Wenn Sie dieses Diagrammfenster geschlossen haben, aktivieren Sie das Kontrollkästchen Frequency resp, um dieses Fenster erneut zu öffnen. Wenn das Diagramm leer ist, klicken Sie im Fenster der App „System Identification“ auf die Modellsymbole, um die Modelle im Diagramm anzuzeigen.

Frequenzgang für die Modelle imp, spad, arxqs und n4s3

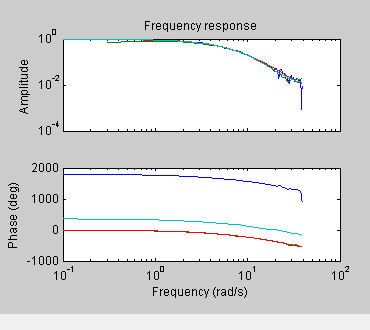
Modellausgangsdiagramm.  Im Fenster „Model Output“ werden Übereinstimmungen zwischen den verschiedenen Modellstrukturen und dem gemessenen Ausgang in den Validierungsdaten angezeigt.

Tipp

Wenn Sie das Fenster „Model Output“ geschlossen haben, aktivieren Sie das Kontrollkästchen Model output, um dieses Fenster erneut zu öffnen. Wenn das Diagramm leer ist, klicken Sie im Fenster der App „System Identification“ auf die Modellsymbole, um die Modelle im Diagramm anzuzeigen.

Gemessener Ausgang und Modellausgang für die Modelle imp, arxqs und n4s3

Im Modellausgangsdiagramm wird die Modellantwort auf den Eingang in den Validierungsdaten angezeigt. Die angepassten Werte für jedes Modell werden im Bereich Best Fits des Fensters „Model Output“ zusammengefasst. Die Modelle in der Liste Best Fits sind vom besten Modell ganz oben bis zum schlechtesten Modell ganz unten angeordnet. Die Übereinstimmung zwischen den beiden Kurven wird berechnet, sodass 100 % eine perfekte Übereinstimmung bedeutet, während 0 für eine schlechte Übereinstimmung steht (d. h., der Modellausgang weist dieselbe Übereinstimmung mit dem gemessenen Ausgang auf wie der Mittelwert des gemessenen Ausgangs).

In diesem Beispiel stimmt der Ausgang der Modelle mit dem Validierungsdatenausgang überein, was darauf hinweist, dass die Modelle die wichtigsten Dynamiken des Systems erfassen und eine lineare Modellierung ausreichend ist.

Tipp

Soll anstelle des simulierten Ausgangs der vorhergesagte Modellausgang verglichen werden, wählen Sie diese Option im Menü Options des Fensters „Model Output“ aus.

Schätzung linearer Modelle

Strategie für die Schätzung genauer Modelle

Die in Schätzung linearer Modelle mithilfe von „Quick Start“ geschätzten linearen Modelle stellen die Dynamiken des Systems in ausreichender Weise dar.

In diesem Teil des Tutorials erhalten Sie genaue parametrische Modelle, indem Sie die folgenden Aufgaben ausführen:

1. Identifizieren anfänglicher Modellordnungen und -verzögerungen anhand Ihrer Daten mithilfe einer einfachen Polynommodellstruktur (ARX).

2. Untersuchen komplexerer Modellstrukturen mit Ordnungen und Verzögerungen in unmittelbarer Nähe der von Ihnen gefundenen Anfangswerte.

Bei den resultierenden Modellen handelt es sich um zeitdiskrete Modelle.

Schätzung möglicher Modellordnungen

Zum Identifizieren von Black-Box-Modellen müssen Sie die Modellordnung angeben. Wie können Sie jedoch feststellen, welche Modellordnungen Sie für Ihre Black-Box-Modelle angeben müssen? Die Antwort auf diese Frage lautet: Sie können einfache Polynommodelle (ARX) für eine Reihe von Ordnungen und Verzögerungen schätzen und die Leistung dieser Modelle vergleichen. Sie wählen die Ordnungen und Verzögerungen, die der besten Modellanpassung entsprechen, als Anfangsvermutung für die genauere Modellierung aus, indem Sie verschiedene Modellstrukturen wie Transferfunktions- und Zustandsraummodelle verwenden.

Infos zu ARX-Modellen.  Für ein Single-Input/Single-Output-(SISO-)System lautet die Struktur des ARX-Modells wie folgt:

$$\begin{array}{l}y(t)+a_{1}y(t-1)+\dots +a_{na}y(t-n_a)=\\ {\text{ b}}_{\text{1}}u(t-n_k)+\dots +b_{nb}u(t-n_k-n_b+1)+e(t)\end{array}$$

y(t) steht dabei für den Ausgang zum Zeitpunkt t, u(t) steht für den Eingang zum Zeitpunkt t, n_a ist die Anzahl der Polstellen, n_b ist die Anzahl der Nullstellen plus 1, n_k ist die Eingangsverzögerung – die Anzahl der Abtastungen, bevor sich der Eingang auf den Systemausgang auswirkt (die sogenannte Verzögerung oder Totzeit des Modells) – und e(t) ist die Störung durch weißes Rauschen.

Sie geben die Modellordnungen n_a, n_b und n_k an, um ARX-Modelle zu schätzen. Das Produkt System Identification Toolbox schätzt die Parameter $$a_1\dots a_n$$ und $$b_1\dots b_n$$ anhand der Daten.

So schätzen Sie Modellordnungen

1. Wählen Sie in der App „System Identification“ die Optionen Estimate > Polynomial Models (Schätzen > Polynommodelle) aus, um das Dialogfenster „Polynomial Models“ (Polynommodelle) zu öffnen.

   

2. Wählen Sie aus der Liste Structure den Eintrag ARX: [na nb nk] aus. Standardmäßig ist dieser bereits ausgewählt.

3. Bearbeiten Sie das Feld Orders (Ordnungen), um alle Kombinationen aus Polstellen, Nullstellen und Verzögerungen auszuprobieren, wobei alle Werte zwischen 1 und 10 liegen:

   [1:10 1:10 1:10]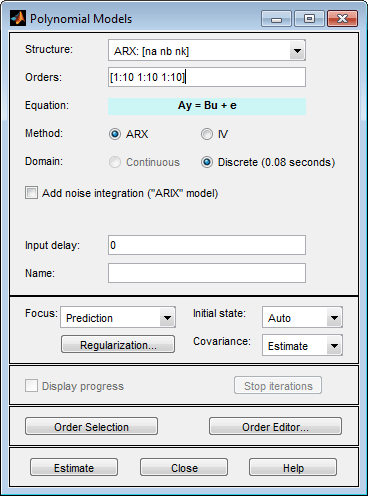

   

4. Klicken Sie auf Estimate (Schätzen), um das Fenster „ARX Model Structure Selection“ (Auswahl der ARX-Modellstruktur) zu öffnen, in dem die Modellleistung für jede Kombination der Modellparameter angezeigt wird.

   Wählen Sie mithilfe dieses Diagramms das am besten geeignete Modell aus.

   

   • Entlang der horizontalen Achse wird die Gesamtzahl der Parameter abgebildet: n_a + n_b.

   • Entlang der vertikalen Achse mit der Beschriftung Unexplained output variance (in %) ist der Teil des Ausgangs abgebildet, der vom Modell nicht erklärt werden kann: der Vorhersagefehler des ARX-Modells für die Anzahl der Parameter, die entlang der horizontalen Achse abgebildet sind.

     Der Vorhersagefehler ist die Summe der Quadrate der Differenzen zwischen dem Validierungsdatenausgang und dem Ausgang der Einen-Schritt-voraus-Vorhersage des Modells.

   • n_k ist die Verzögerung.

   Im Diagramm sind drei Rechtecke grün, blau und rot hervorgehoben. Jede Farbe weist wie folgt auf einen Typ der am besten geeigneten Kriterien hin:

   • Rot: beste Übereinstimmung, minimiert die Summe der Quadrate der Differenz zwischen dem Validierungsdatenausgang und dem Modellausgang. Dieses Rechteck gibt die beste Übereinstimmung insgesamt an.

   • Grün: beste Übereinstimmung, minimiert das Rissanen-MDL-Kriterium.

   • Blau: beste Übereinstimmung, minimiert das Akaike-AIC-Kriterium.

   In diesem Tutorial bleibt der Wert Unexplained output variance (in %) (Unerklärte Ausgangsvarianz (in %)) für die gesamte Anzahl der Parameter von 4 bis 20 in etwa konstant. Eine solche Konstanz weist darauf hin, dass sich die Modellleistung bei höheren Ordnungen nicht verbessert. Daher können Modelle niedriger Ordnungen ebenso gut zu den Daten passen.

   Hinweis

   Wenn Sie denselben Datensatz für die Schätzung und die Validierung verwenden, wählen Sie die Modellordnungen mithilfe der MDL- und AIC-Kriterien aus. Diese Kriterien kompensieren die Überanpassung, die sich aus der Verwendung zu vieler Parameter ergibt. Weitere Informationen zu diesen Kriterien finden Sie auf der Referenzseite zu selstruc.

5. Klicken Sie im Fenster „ARX Model Structure Selection“ auf den roten Balken (entspricht dem Wert 15 auf der horizontalen Achse) und klicken Sie anschließend auf Insert (Einfügen). Durch diese Auswahl werden n_a=6, n_b=9 und n_k=2 in das Fenster „Polynomial Models“ eingefügt und die Schätzung wird ausgeführt.

   Bei diesem Vorgang wird das Modell arx692 der App „System Identification“ hinzugefügt und die Diagramme werden aktualisiert, um die Antwort des Modells zu berücksichtigen.

   Hinweis

   Der Standardname des parametrischen Modells umfasst den Modelltyp und die Anzahl der Polstellen, Nullstellen sowie die Verzögerungen. Beispielsweise ist arx692 ein ARX-Modell mit n_a=6, n_b=9 und einer Verzögerung von zwei Abtastungen.

6. Klicken Sie im Fenster „ARX Model Structure Selection“ auf den dritten Balken, der dem Parameter 4 auf der horizontalen Achse entspricht (die niedrigste Ordnung, die noch immer eine gute Übereinstimmung bietet), und klicken Sie anschließend auf Insert.

   • Durch diese Auswahl werden n_a=2, n_b=2 und n_k=3 (eine Verzögerung von drei Abtastungen) in das Fenster „Polynomial Models“ eingefügt und die Schätzung wird ausgeführt.

   • Das Modell arx223 wird der App „System Identification“ hinzugefügt und die Diagramme werden aktualisiert, um die Antwort und den Ausgang des Modells zu berücksichtigen.

7. Klicken Sie auf Close, um das Fenster „ARX Model Structure Selection“ zu schließen.

8. Klicken Sie auf Close, um das Dialogfenster „Polynomial Models“ zu schließen.

Identifizierung von Transferfunktionsmodellen

Durch die Schätzung von ARX-Modellen für verschiedene Ordnungskombinationen, wie in Schätzung möglicher Modellordnungen beschrieben, haben Sie die Anzahl der Polstellen, Nullstellen und die Verzögerungen identifiziert, die einen guten Ausgangspunkt für die systematische Untersuchung verschiedener Modelle darstellen.

Die beste Übereinstimmung insgesamt für dieses System entspricht einem Modell mit sechs Polstellen, neun Nullstellen und einer Verzögerung von zwei Abtastungen. Außerdem hat sich gezeigt, dass ein Modell niedriger Ordnung mit n_a = 2 (zwei Polstellen), n_b = 2 (eine Nullstelle) und n_k = 3 (Eingangs-/Ausgangsverzögerung) ebenfalls eine gute Übereinstimmung bietet. Daher sollten Sie Modellordnungen mit ähnlichen Werten untersuchen.

In diesem Teil des Tutorials schätzen Sie ein Transferfunktionsmodell.

Infos zu Transferfunktionsmodellen.  Die allgemeine Struktur eines Transferfunktionsmodells sieht wie folgt aus:

$$Y(s)=\frac{num(s)}{den(s)}U(s)+E(s)$$

Y(s), U(s) und E(s) stellen die Laplace-Transformationen des Ausgangs, Eingangs bzw. Fehlers dar. num(s) und den(s) stellen die Zähler- und Nennerpolynome dar, die die Beziehung zwischen dem Eingang und dem Ausgang definieren. Die Wurzeln des Nennerpolynoms werden auch als Polstellen des Modells bezeichnet. Die Wurzeln des Zählerpolynoms werden als Nullstellen des Modells bezeichnet.

Sie müssen zur Schätzung eines Transferfunktionsmodells die Anzahl der Polstellen und Nullstellen angeben. Das Produkt System Identification Toolbox schätzt die Zähler- und Nennerpolynome sowie die Eingangs-/Ausgangsverzögerungen anhand der Daten.

Die Struktur des Transferfunktionsmodells eignet sich gut für eine schnelle Schätzung, weil es ausreicht, wenn Sie am Anfang nur zwei Parameter angeben: np ist die Anzahl der Polstellen und nz ist die Anzahl der Nullstellen.

So schätzen Sie Transferfunktionsmodelle

1. Wählen Sie in der App „System Identification“ die Optionen Estimate > Transfer Function Models (Schätzen > Transferfunktionsmodelle) aus, um das Dialogfenster „Transfer Functions“ (Transferfunktionen) zu öffnen.

   

2. Geben Sie im Dialogfenster „Estimate Transfer Functions“ (Transferfunktionen schätzen) folgende Optionen an:

   • Number of poles: Lassen Sie den Standardwert 2 unverändert, um eine Funktion zweiter Ordnung für zwei Polstellen anzugeben.

   • Number of zeros: Lassen Sie den Standardwert 1 unverändert.

   • Continuous-time: Lassen Sie dieses Kontrollkästchen aktiviert.

3. Klicken Sie auf Delay, um den Bereich zur Angabe der Eingangs-/Ausgangsverzögerungen zu erweitern.

   Durch die Schätzung von ARX-Modellen für verschiedene Ordnungskombinationen, wie in Schätzung möglicher Modellordnungen beschrieben, haben Sie eine Verzögerung von 3 Abtastungen (nk = 3) identifiziert. Diese Verzögerung wird in eine zeitkontinuierliche Verzögerung von (nk-1)*Ts übersetzt, was 0,16 Sekunden entspricht.

   Geben Sie für Delay einen Wert von 0.16 Sekunden an. Lassen Sie Fixed aktiviert.

   Verwenden Sie die Standard-Schätzungsoptionen im Bereich „Estimation Options“. Standardmäßig weist die App dem Modell den Namen tf1 zu. Das Dialogfenster sollte wie folgt aussehen.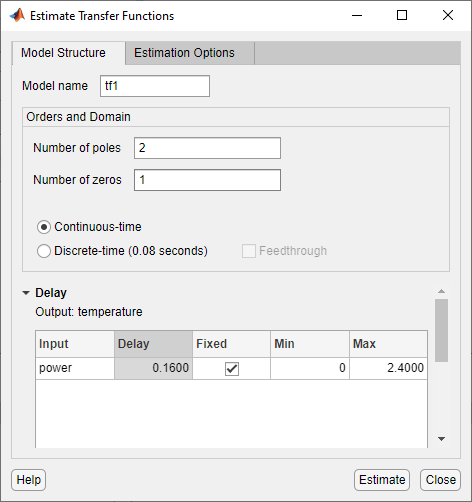

   

4. Klicken Sie auf Estimate, um der App „System Identification“ ein Transferfunktionsmodell mit dem Namen tf1 hinzuzufügen. Im Fenster „Model Output“ (Modellausgang) können Sie den Ausgang der Schätzung des Transferfunktionsmodells im Vergleich zu den Schätzungen anderer Modelle anzeigen.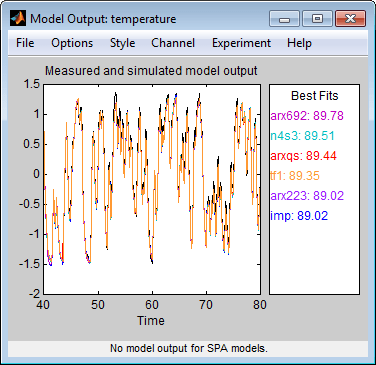

   

   Tipp

   Wenn Sie das Fenster „Model Output“ geschlossen haben, können Sie es wieder öffnen, indem Sie das Kontrollkästchen Model output in der App „System Identification“ aktivieren. Wenn das neue Modell nicht im Diagramm angezeigt wird, klicken Sie in der App „System Identification“ auf das Modellsymbol, um das Modell zu aktivieren.

5. Klicken Sie auf Close, um das Dialogfenster „Transferfunktionen“ zu schließen.

Weitere Informationen.  Weitere Informationen zum Identifizieren von Transferfunktionsmodellen finden Sie unter Transfer Function Models.

Identifizieren von Zustandsraummodellen

Durch die Schätzung von ARX-Modellen für verschiedene Ordnungskombinationen, wie in Schätzung möglicher Modellordnungen beschrieben, haben Sie die Anzahl der Polstellen, Nullstellen und die Verzögerungen identifiziert, die einen guten Ausgangspunkt für die systematische Untersuchung verschiedener Modelle darstellen.

Die beste Übereinstimmung insgesamt für dieses System entspricht einem Modell mit sechs Polstellen, neun Nullstellen und einer Verzögerung von zwei Abtastungen. Außerdem hat sich gezeigt, dass ein Modell niedriger Ordnung mit n_a = 2 (zwei Polstellen), n_b = 2 (eine Nullstelle) und n_k = 3 (Eingangs-/Ausgangsverzögerung) ebenfalls eine gute Übereinstimmung bietet. Daher sollten Sie Modellordnungen mit ähnlichen Werten untersuchen.

In diesem Teil des Tutorials schätzen Sie ein Zustandsraummodell.

Infos zu Zustandsraummodellen.  Die allgemeine Struktur eines Zustandsraummodells (Innovationsform) sieht wie folgt aus:

$$\begin{array}{l}\frac{dx}{dt}=Ax(t)+Bu(t)+Ke(t)\\ y(t)=Cx(t)+Du(t)+e(t)\end{array}$$

y(t) steht dabei für den Ausgang zum Zeitpunkt t, u(t) steht für den Eingang zum Zeitpunkt t, x(t) ist der Zustandsvektor zum Zeitpunkt t und e(t) ist die Störung durch weißes Rauschen.

Sie müssen zur Schätzung eines Zustandsraummodells eine einzelne Ganzzahl als Modellordnung (Dimension des Zustandsvektors) angeben. Das Produkt System Identification Toolbox schätzt die Zustandsraummatrizen A, B, C, D und K anhand der Daten.

Die Struktur des Zustandsraummodells eignet sich gut für eine schnelle Schätzung, weil es ausreicht, wenn Sie am Anfang nur die Anzahl der Zustände (die gleich der Anzahl der Polstellen ist) angeben. Optional können Sie auch die Verzögerungen und das Durchgriffsverhalten angeben.

So schätzen Sie Zustandsraummodelle

1. Wählen Sie in der App „System Identification“ die Optionen Estimate > State Space Models (Schätzen > Zustandsraummodelle) aus, um das Dialogfenster „State Space Models“ zu öffnen.

   

2. Geben Sie im Feld Specify value auf der Registerkarte Model Structure die Modellordnung an. Geben Sie 6 an, um ein Zustandsraummodell sechster Ordnung zu erstellen.

   Diese Auswahl basiert auf der Tatsache, dass das ARX-Modell mit der besten Übereinstimmung sechs Polstellen aufweist.

   Tipp

   Zwar wird in diesem Tutorial ein Zustandsraummodell sechster Ordnung geschätzt, aber Sie könnten auch untersuchen, ob auch ein Modell niedrigerer Ordnung die Systemdynamiken ausreichend darstellt.

   Das Dialogfenster sollte wie folgt aussehen:

   

3. Wählen Sie die Registerkarte Estimation Options (Schätzoptionen) aus, um zusätzliche Optionen anzuzeigen.

4. Ändern Sie Estimation Focus (Schätzungsfokus) in Simulation, um das Modell für den Einsatz bei der Ausgangssimulation zu optimieren.

   Das Dialogfenster „State Space Models“ (Zustandsraummodelle) sieht in etwa wie in der folgenden Abbildung aus.

   

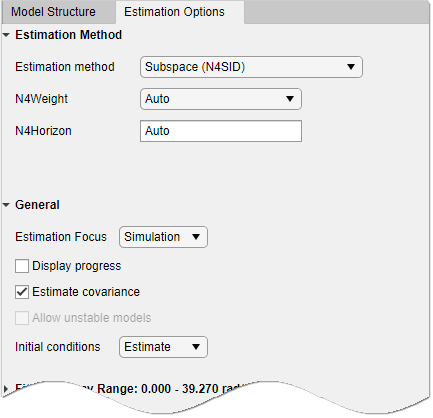
5. Klicken Sie auf Estimate, um der App „System Identification“ ein Zustandsraummodell mit dem Namen ss1 hinzuzufügen.

   Im Fenster „Model Output“ (Modellausgang) können Sie den Ausgang der Schätzung des Zustandsraummodells im Vergleich zu den Schätzungen anderer Modelle anzeigen.

   

   Tipp

   Wenn Sie das Fenster „Model Output“ geschlossen haben, können Sie es wieder öffnen, indem Sie das Kontrollkästchen Model output in der App „System Identification“ aktivieren. Wenn das neue Modell nicht im Diagramm angezeigt wird, klicken Sie in der App „System Identification“ auf das Modellsymbol, um das Modell zu aktivieren.

6. Klicken Sie auf Close, um das Dialogfenster „State Space Models“ zu schließen.

Weitere Informationen.  Weitere Informationen zum Identifizieren von Zustandsraummodellen finden Sie unter State-Space Models.

Identifizieren von ARMAX-Modellen

Durch die Schätzung von ARX-Modellen für verschiedene Ordnungskombinationen, wie in Schätzung möglicher Modellordnungen beschrieben, haben Sie die Anzahl der Polstellen, Nullstellen und die Verzögerungen identifiziert, die einen guten Ausgangspunkt für die systematische Untersuchung verschiedener Modelle darstellen.

Die beste Übereinstimmung insgesamt für dieses System entspricht einem Modell mit sechs Polstellen, neun Nullstellen und einer Verzögerung von zwei Abtastungen. Außerdem hat sich gezeigt, dass ein Modell niedriger Ordnung mit n_a = 2 (zwei Polstellen), n_b = 2 (eine Nullstelle) und n_k = 3 ebenfalls eine gute Übereinstimmung bietet. Daher sollten Sie Modellordnungen mit ähnlichen Werten untersuchen.

In diesem Teil des Tutorials schätzen Sie ein ARMAX-Eingangs-/Ausgangs-Polynommodell.

Infos zu ARMAX-Modellen.  Für ein Single-Input/Single-Output-(SISO-)System lautet die Struktur des ARMAX-Polynommodells wie folgt:

$$\begin{array}{l}y(t)+a_{1}y(t-1)+\dots +a_{na}y(t-n_a)=\\ {\text{ b}}_{\text{1}}u(t-n_k)+\dots +b_{nb}u(t-n_k-n_b+1)+\\ e(t)+c_{1}e(t-1)+\dots +c_{nc}e(t-n_c)\end{array}$$

y(t) steht dabei für den Ausgang zum Zeitpunkt t, u(t) steht für den Eingang zum Zeitpunkt t, n_a ist die Anzahl der Polstellen für das dynamische Modell, n_b ist die Anzahl der Nullstellen plus 1, n_c ist die Anzahl der Polstellen für das Störungsmodell, n_k ist die Anzahl der Abtastungen, bevor sich der Eingang auf den Ausgang des Systems auswirkt (die sogenannte Verzögerung oder Totzeit des Modells), und e(t) ist die Störung durch weißes Rauschen.

Hinweis

Das ARMAX-Modell ist flexibler als das ARX-Modell, weil die ARMAX-Struktur ein zusätzliches Polynom enthält, um die additive Störung zu modellieren.

Zum Schätzen von ARMAX-Modellen müssen Sie die Modellordnungen angeben. Das Produkt System Identification Toolbox schätzt die Modellparameter $$a_1\dots a_n$$, $$b_1\dots b_n$$ und $$c_1\dots c_n$$ anhand der Daten.

So schätzen Sie ARMAX-Modelle

1. Wählen Sie in der App „System Identification“ die Optionen Estimate > Polynomial Models (Schätzen > Polynommodelle) aus, um das Dialogfenster „Polynomial Models“ (Polynommodelle) zu öffnen.

   

2. Wählen Sie aus der Liste Structure den Eintrag ARMAX: [na nb nc nk] aus, um ein ARMAX-Modell zu schätzen.

   

3. Legen Sie im Feld Orders für die Ordnungen na, nb, nc und nk die folgenden Werte fest:

   [2 2 2 2]

   Die App weist dem Modell amx2222 standardmäßig den Namen zu, der im Feld Name angezeigt wird.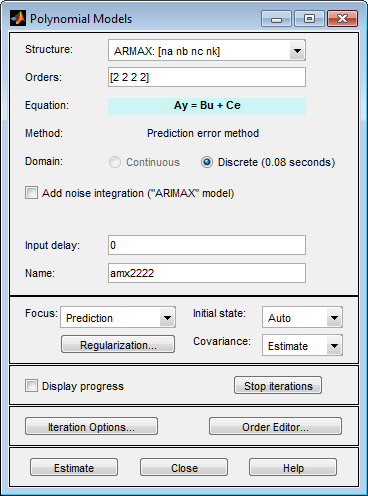

   

4. Klicken Sie auf Estimate, um das ARMAX-Modell zur App „System Identification“ hinzuzufügen.

5. Wiederholen Sie die Schritte 3 und 4 mit höheren Ordnungen (Orders 3 3 2 2). Diese Ordnungen ergeben ein Modell, das fast genauso gut zu den Daten passt wie das ARX-Model arx692 höherer Ordnung.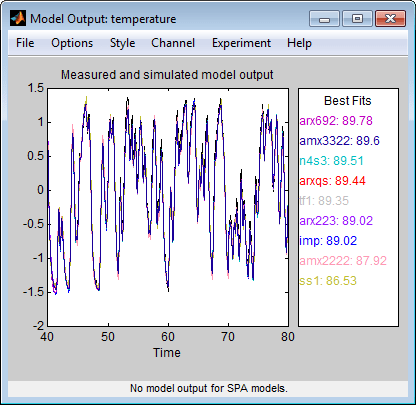

   

   Tipp

   Wenn Sie das Fenster „Model Output“ geschlossen haben, können Sie es wieder öffnen, indem Sie das Kontrollkästchen Model output in der App „System Identification“ aktivieren. Wenn das neue Modell nicht im Diagramm angezeigt wird, klicken Sie in der App „System Identification“ auf das Modellsymbol, um das Modell zu aktivieren.

6. Klicken Sie auf Close, um das Dialogfenster „Polynomial Models“ zu schließen.

Weitere Informationen.  Ausführliche Informationen zum Identifizieren von Eingangs-/Ausgangs-Polynommodellen wie z. B. ARMAX, finden Sie unter Input-Output Polynomial Models.

Auswählen des besten Modells

Sie können Modelle vergleichen, um das Modell mit der besten Leistung auszuwählen.

Sie müssen die Modelle bereits geschätzt haben, wie in Schätzung linearer Modelle beschrieben.

Falls Sie diesen Schritt noch ausführen müssen, klicken Sie hier.

Modellübersicht.  Die folgende Abbildung zeigt die App „System Identification“, die alle in Schätzung linearer Modelle geschätzten Modelle enthält.

Untersuchen des Modellausgangs.  Untersuchen Sie das Modellausgangsdiagramm, um festzustellen, inwieweit der Modellausgang mit dem gemessenen Ausgang im Validierungsdatensatz übereinstimmt. Ein gutes Modell ist das einfachste Modell, das die Dynamiken am besten beschreibt und den Ausgang für verschiedene Eingänge erfolgreich simuliert oder vorhersagt. Modelle werden im Bereich Best Fits des Diagramms „Model Output“ nach Namen aufgeführt. Beachten Sie, dass eines der einfacheren Modelle, amx3322, eine ähnliche Übereinstimmung ergab wie das von Ihnen erstellte Modell arx692 mit der höchsten Ordnung.

Tipp

Wenn Sie das Fenster „Model Output“ geschlossen haben, können Sie es wieder öffnen, indem Sie das Kontrollkästchen Model output in der App „System Identification“ aktivieren. Wenn das neue Modell nicht im Diagramm angezeigt wird, klicken Sie in der App „System Identification“ auf das Modellsymbol, um das Modell zu aktivieren.

Zum Validieren Ihrer Modelle mithilfe eines anderen Datensatzes können Sie diesen Datensatz per Drag and Drop auf das Rechteck Validation Data in der App „System Identification“ ziehen. Wenn Sie Validierungsdaten in die Frequenzdomäne transformieren, wird das Diagramm „Model Output“ aktualisiert und zeigt den Modellvergleich in der Frequenzdomäne an.

Um die Übereinstimmung dieser Modelle mit den Daten genauer zu betrachten, vergrößern Sie einen Teil des Diagramms, indem Sie klicken und ein Rechteck um den Bereich von Interesse ziehen, wie in der folgenden Abbildung veranschaulicht.

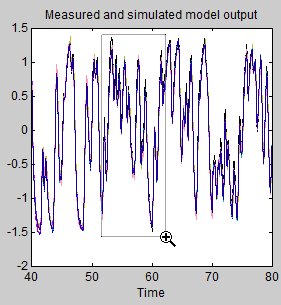
Wenn Sie die Maustaste loslassen, wird dieser Bereich vergrößert und es wird deutlich, dass der Ausgang aller Modelle ebenfalls gut zu den Validierungsdaten passt.

Anzeigen von Modellparametern

Anzeigen von Modellparameterwerten

Sie können die numerischen Parameterwerte für jedes geschätzte Modell anzeigen.

Sie müssen die Modelle bereits geschätzt haben, wie in Schätzung linearer Modelle beschrieben.

Falls Sie diesen Schritt noch ausführen müssen, klicken Sie hier.

Zum Anzeigen der Parameterwerte des Modells amx3322 klicken Sie in der App „System Identification“ mit der rechten Maustaste auf das Modellsymbol. Das Dialogfenster „Data/model Info“ wird geöffnet.

Im nicht editierbaren Bereich des Dialogfensters „Data/model Info“ sind die Parameterwerte aufgelistet, die der folgenden Differenzengleichung für Ihr System entsprechen:

$$\begin{array}{l}y(t)-1.502y(t-1)+0.7193y(t-2)-0.1179y(t-3)=\\ 0.003956u(t-2)+0.06245u(t-3)+0.02673u(t-4)+e(t)-0.5626e(t-1)+0.2355e(t-2)\end{array}$$

Hinweis

Der Koeffizient von u(t-2) unterscheidet sich nicht wesentlich von null. Diese fehlende Differenz erklärt, warum Verzögerungswerte von 2 und 3 zu guten Ergebnissen führen.

Parameterwerte werden im folgenden Format angezeigt:

$$\begin{array}{l}A(z)=1+a_1{z}^{-1}+\dots +a_{na}{z}^{-na}\\ B(z)=b_1{z}^{-nk}+\dots +b_{nb}{z}^{-nb-nk+1}\\ C(z)=1+c_1{z}^{-1}+\dots +c_{nc}{z}^{-nc}\end{array}$$

Die Parameter werden in der ARMAX-Modellstruktur wie folgt angezeigt:

$$A(q)y(t)=B(q)u(t)+C(q)e(t)$$

Dies entspricht dieser allgemeinen Differenzengleichung:

$$\begin{array}{l}y(t)+a_{1}y(t-1)+\dots +a_{na}y(t-n_a)=\\ {\text{ b}}_{\text{1}}u(t-n_k)+\dots +b_{nb}u(t-n_k-n_b+1)+\\ e(t)+c_{1}e(t-1)+\dots +c_{nc}e(t-n_c)\end{array}$$

y(t) steht dabei für den Ausgang zum Zeitpunkt t, u(t) steht für den Eingang zum Zeitpunkt t, n_a ist die Anzahl der Polstellen für das dynamische Modell, n_b ist die Anzahl der Nullstellen plus 1, n_c ist die Anzahl der Polstellen für das Störungsmodell, n_k ist die Anzahl der Abtastungen, bevor sich der Eingang auf den Ausgang des Systems auswirkt (die sogenannte Verzögerung oder Totzeit des Modells), und e(t) ist die Störung durch weißes Rauschen.

Anzeigen von Parameterunsicherheiten

Sie können Parameterunsicherheiten geschätzter Modelle anzeigen.

Sie müssen die Modelle bereits geschätzt haben, wie in Schätzung linearer Modelle beschrieben.

Falls Sie diesen Schritt noch ausführen müssen, klicken Sie hier. Zum Anzeigen der Parameterwerte des Modells amx3322 klicken Sie in der App „System Identification“ mit der rechten Maustaste auf das Modellsymbol. Das Dialogfenster „Data/model Info“ wird geöffnet.

Zum Anzeigen von Parameterunsicherheiten klicken Sie im Dialogfenster „Data/model Info“ auf Present (Darstellen) und zeigen Sie die Modellinformationen an der MATLAB-Eingabeaufforderung an.

amx3322 =                                                                     
Discrete-time ARMAX model:  A(z)y(t) = B(z)u(t) + C(z)e(t)                    
                                                                              
  A(z) = 1 - 1.502 (+/- 0.05982) z^-1 + 0.7193 (+/- 0.0883) z^-2             
                                   - 0.1179 (+/- 0.03462) z^-3                
                                                                              
                                                                              
  B(z) = 0.003956 (+/- 0.001551) z^-2 + 0.06245 (+/- 0.002372) z^-3           
                                 + 0.02673 (+/- 0.005651) z^-4                
                                                                              
                                                                              
  C(z) = 1 - 0.5626 (+/- 0.07322) z^-1 + 0.2355 (+/- 0.05294) z^-2            
                                                                              
Name: amx3322                                                                 
Sample time: 0.08 seconds                                                     
                                                                              
Parameterization:                                                             
   Polynomial orders:   na=3   nb=3   nc=2   nk=2                             
   Number of free coefficients: 8                                             
   Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
                                                                              
Status:                                                                       
Termination condition: Near (local) minimum, (norm(g) < tol).                 
Number of iterations: 5, Number of function evaluations: 11                   
                                                                              
Estimated using POLYEST on time domain data "data_est".                       
Fit to estimation data: 95.3% (prediction focus)                              
FPE: 0.001596, MSE: 0.001546                                                   
More information in model's "Report" property. 

Die Unsicherheit von 1 Standardabweichung für die Modellparameter wird in Klammern neben den einzelnen Parameterwerten angegeben.

Exportieren des Modells in den MATLAB-Arbeitsbereich

Die Modelle, die Sie in der App „System Identification“ erstellen, stehen nicht automatisch im MATLAB-Arbeitsbereich zur Verfügung. Wenn ein Modell für andere Toolboxen sowie für die Befehle von Simulink^® und System Identification Toolbox verfügbar sein soll, müssen Sie das Modell aus der App „System Identification“ in den MATLAB-Arbeitsbereich exportieren. Handelt es sich bei dem Modell beispielsweise um eine Anlage, die eine Steuerung benötigt, können Sie das Modell aus dem MATLAB-Arbeitsbereich in das Produkt Control System Toolbox™ importieren.

Sie müssen die Modelle bereits geschätzt haben, wie in Schätzung linearer Modelle beschrieben.

Falls Sie diesen Schritt noch ausführen müssen, klicken Sie hier.

Zum Exportieren des Modells amx3322 ziehen Sie es auf das Rechteck To Workspace in der App „System Identification“. Klicken Sie alternativ im Dialogfenster „Data/model Info“ auf Export.

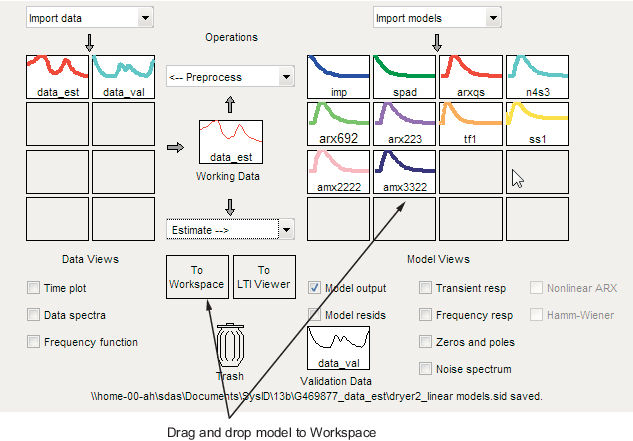
Das Modell wird im Browser des MATLAB-Arbeitsbereichs angezeigt.

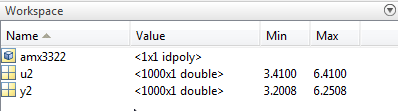
Hinweis

Bei diesem Modell handelt es sich um ein idpoly-Modellobjekt.

Sobald sich das Modell im MATLAB-Arbeitsbereich befindet, können Sie weitere Operationen am Modell ausführen. Wenn Sie beispielsweise das Produkt Control System Toolbox installiert haben, können Sie das Modell mit dem folgenden Befehl in ein Zustandsraummodell transformieren:

ss_model=ss(amx3322)

Exportieren des Modells in den Linear System Analyzer

Wenn das Produkt Control System Toolbox installiert ist, wird das Rechteck To Linear System Analyzer in der App „System Identification“ angezeigt.

Der Linear System Analyzer ist eine grafische Benutzeroberfläche für die Anzeige und Bearbeitung von Antwortdiagrammen linearer Modelle. Er zeigt die folgenden Diagramme an:

• Sprung- und Impulsantwort

• Bode, Nyquist und Nichols

• Frequenzgang-Singulärwerte

• Polstellen/Nullstellen

• Antwort auf allgemeine Eingangssignale

• Nicht erzwungene Antwort, ausgehend von bestimmten Anfangszuständen (nur für Zustandsraummodelle)

Zum Plotten eines Modells im Linear System Analyzer ziehen Sie das Modellsymbol per Drag and Drop auf das Rechteck To Linear System Analyzer in der App „System Identification“. Klicken Sie alternativ im Dialogfenster „Data/model Info“ auf Show in Linear System Analyzer (In Linear System Analyzer anzeigen).

Weitere Informationen zum Arbeiten mit Diagrammen im Linear System Analyzer finden Sie unter Linear System Analyzer Overview (Control System Toolbox).