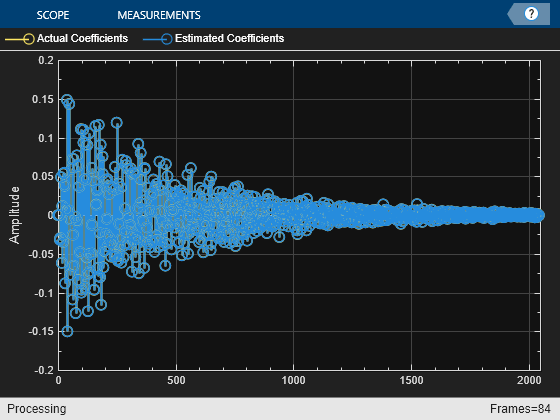
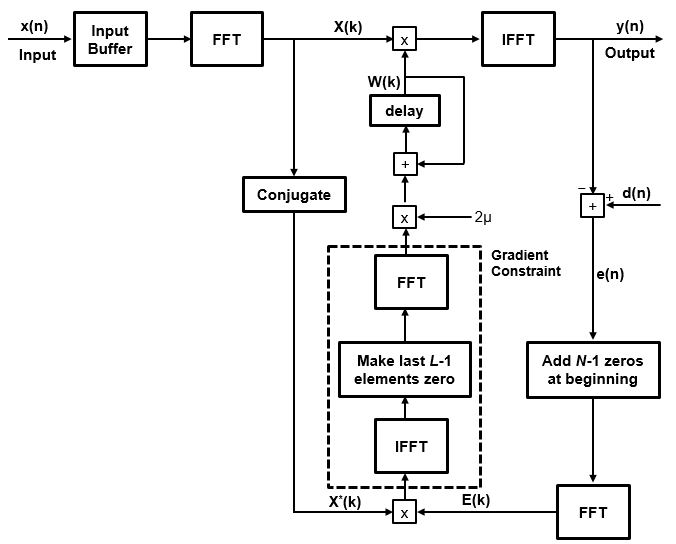
dsp.FrequencyDomainAdaptiveFilter
Compute output, error, and coefficients using frequency-domain FIR adaptive filter
Description
The dsp.FrequencyDomainAdaptiveFilter
System object™ implements an adaptive finite impulse response (FIR) filter in the frequency
domain using the fast block least mean squares (LMS) algorithm. The Length and
the BlockLength properties specify the filter length and the
block length values the algorithm uses. The FFTCoefficients property contains the discrete Fourier
transform of the current filter coefficients. The object offers the constrained and
unconstrained versions of the algorithm with partitioned and non-partitioned modes. For
details, see Algorithms.
To filter a signal using frequency-domain FIR adaptive filter:
Create the
dsp.FrequencyDomainAdaptiveFilterobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
fdaf = dsp.FrequencyDomainAdaptiveFilterfdaf. This System object is used to compute the filtered output and the filter error for a given
input and desired signal.
fdaf = dsp.FrequencyDomainAdaptiveFilter(len)Length
property set to len.
fdaf = dsp.FrequencyDomainAdaptiveFilter(___,Name,Value)
Example: fdaf =
dsp.FrequencyDomainAdaptiveFilter('Length',32,'StepSize',0.1) models a
frequency-domain adaptive filter with a length of 32 taps and a step size of
0.1.
Properties
Usage
Syntax
Description
[
filters the input signal, y,err] = fdaf(x,d)x, using d as the
desired signal, and returns the filtered output in y and the filter
error in err. The System object estimates the filter weights needed to minimize the error between the output
signal and the desired signal. The FFT of these filter weights can be obtained by
accessing the FFTCoefficients property after calling the object
algorithm.
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Algorithms
References
[1] Shynk, J.J. "Frequency-Domain and Multirate Adaptive Filtering." IEEE Signal Processing Magazine. Vol. 9, Number 1, 1992, pp. 14–37.
[2] Farhang-Boroujeny, B., Adaptive Filters: Theory and Applications, Chichester, England, Wiley, 1998.
[3] Stockham, T. G., Jr. "High Speed Convolution and Correlation." Proceedings of the 1966 Spring Joint Computer Conference, AFIPS, Vol. 28, 1966, pp. 229–233.
Extended Capabilities
Version History
Introduced in R2013b
See Also
Objects
dsp.LMSFilter|dsp.RLSFilter|dsp.AffineProjectionFilter|dsp.AdaptiveLatticeFilter|dsp.FilteredXLMSFilter|dsp.FIRFilter|dsp.FastTransversalFilter|dsp.FrequencyDomainFIRFilter

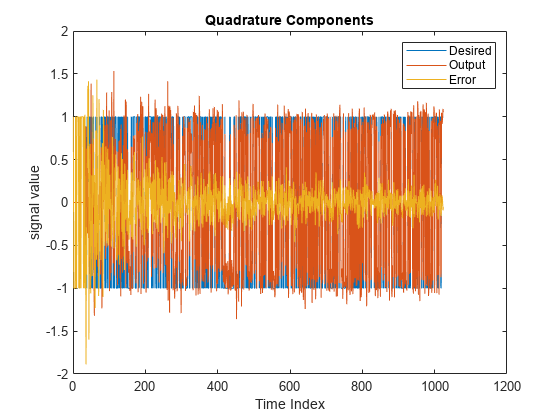
![Figure contains an axes object. The axes object with title Received Signal Scatter Plot, xlabel Real[x], ylabel Imag[x] contains a line object which displays its values using only markers.](../../examples/dsp/win64/QPSKAdaptiveEqualizationWithFIRFilterExample_03.png)
![Figure contains an axes object. The axes object with title Desired Signal Scatter Plot, xlabel Real[y], ylabel Imag[y] contains a line object which displays its values using only markers.](../../examples/dsp/win64/QPSKAdaptiveEqualizationWithFIRFilterExample_04.png)
![Figure contains an axes object. The axes object with title Equalized Signal Scatter Plot, xlabel Real[y], ylabel Imag[y] contains a line object which displays its values using only markers.](../../examples/dsp/win64/QPSKAdaptiveEqualizationWithFIRFilterExample_05.png)