Bewertung von Amplituden- und Phasenrändern
Dieses Beispiel zeigt, wie man die Auswirkung von Stabilitätsreserven auf die Reaktionscharakteristik eines Kontrollsystems im geschlossenen Regelkreis untersucht.
Stabilität einer Rückkopplungsschleife
Stabilität bedeutet im Allgemeinen, dass alle internen Signale begrenzt bleiben. Dies ist eine Standardanforderung an Kontrollsysteme zur Vermeidung von Kontrollverlusten und Schäden an Geräten. Bei linearen Rückkopplungssystemen kann die Stabilität anhand der Polstellen der Transferfunktion des geschlossenen Regelkreises beurteilt werden. Betrachten Sie zum Beispiel die SISO-Rückkopplungsschleife:

Abbildung 1: SISO-Rückkopplungsschleife.
Für die Einheitsschleifenverstärkung k können Sie die Transferfunktion des geschlossenen Regelkreises T folgendermaßen berechnen:
G = tf([.5 1.3],[1 1.2 1.6 0]); T = feedback(G,1);
Um die Pole von T zu erhalten, geben Sie ein:
pole(T)
ans = -0.2305 + 1.3062i -0.2305 - 1.3062i -0.7389 + 0.0000i
Die Rückkopplungsschleife für k=1 ist stabil, da alle Pole negative Realteile haben.
Wie stabil ist stabil?
Die Überprüfung der Pole im geschlossenen Regelkreis liefert uns eine binäre Bewertung der Stabilität. In der Praxis ist es oft hilfreicher, die Robustheit (oder Fragilität) der Stabilität zu kennen. Einen Hinweis auf die Robustheit gibt die mögliche Veränderung der Schleifenverstärkung, bevor die Stabilität verloren geht. Sie können ein Wurzelortdiagramm verwenden, um den Bereich der k-Werte einzuschätzen, für die die Schleife stabil ist:
rlocus(G)

Wenn Sie auf den Punkt klicken, an dem die Ortskurve die y-Achse schneidet, sehen Sie, dass diese Rückkopplungsschleife stabil ist, wenn gilt:

Dieser Bereich zeigt, dass bei k=1 die Schleifenverstärkung um 270% zunehmen kann, bevor die Stabilität verloren geht.
Amplituden- und Phasenränder
Veränderungen in der Schleifenverstärkung sind nur ein Aspekt einer robusten Stabilität. Im Allgemeinen bedeutet die nicht perfekte Modellierung der Regelstrecke, dass sowohl Verstärkung als auch Phase nicht genau bekannt sind. Da Modellierungsfehler in der Nähe der Verstärkungsübergangsfrequenz (Frequenz, bei der die offene Verstärkung 0 dB beträgt) am schädlichsten sind, ist es auch wichtig, wie viel Phasenabweichung bei dieser Frequenz toleriert werden kann.
Der Phasenrand gibt an, wie viel Phasenabweichung bei der Verstärkungsübergangsfrequenz nötig ist, damit die Stabilität verloren geht. In ähnlicher Weise gibt der Amplitudenrand an, wie viel relative Amplitudenabweichung bei der Phasenübergangsfrequenz nötig ist, damit die Stabilität verloren geht. Gemeinsam ergeben diese beiden Zahlen eine Schätzung der „Sicherheitsmarge“ hinsichtlich der Stabilität des geschlossenen Regelkreises. Je kleiner die Stabilitätsreserven sind, desto anfälliger ist die Stabilität.
Sie können die Amplituden- und Phasenränder folgendermaßen auf einem Bode-Diagramm darstellen. Erstellen Sie zunächst das Diagramm:
bode(G), grid

Rechtsklicken Sie dann auf das Diagramm und wählen Sie das Untermenü Characteristics -> Minimum Stability Margins (Merkmale -> Minimale Stabilitätsreserven). Klicken Sie schließlich auf die blauen Punktmarkierungen. Das resultierende Diagramm ist unten abgebildet:
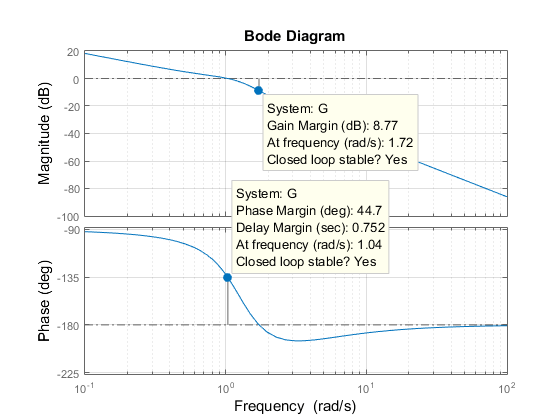
Das bedeutet einen Amplitudenrand von etwa 9 dB und einen Phasenrand von etwa 45 Grad. Die entsprechende Sprungantwort des geschlossenen Regelkreises weist ein Überschwingen von etwa 20% und einige Oszillationen auf.
step(T), title('Closed-loop response for k=1')

Wenn die Verstärkung auf k=2 erhöht wird, reduzieren sich die Stabilitätsreserven auf
[Gm,Pm] = margin(2*G); GmdB = 20*log10(Gm) % gain margin in dB Pm % phase margin in degrees
GmdB =
2.7435
Pm =
8.6328
und die Reaktion im geschlossenen Regelkreis weist schlecht gedämpfte Oszillationen auf, ein Vorzeichen einer drohenden Instabilität.
step(feedback(2*G,1)), title('Closed-loop response for k=2')

Systeme mit mehreren Verstärkungs- oder Phasenübergängen
Einige Systeme haben mehrere Verstärkungs- oder Phasenübergangsfrequenzen, was zu mehreren Werten des Amplituden- oder Phasenrands führt. Betrachten Sie zum Beispiel die Rückkopplungsschleife

Abbildung 2: Rückkopplungsschleife mit mehreren Phasenübergängen
Die Reaktion im geschlossenen Regelkreis für k=1 ist stabil:
G = tf(20,[1 7]) * tf([1 3.2 7.2],[1 -1.2 0.8]) * tf([1 -8 400],[1 33 700]);
T = feedback(G,1);
step(T), title('Closed-loop response for k=1')

Plotten Sie zur Beurteilung der Stabilität dieses Regelkreises seine Bode-Antwort:
bode(G), grid

Rechtsklicken Sie dann auf das Diagramm und wählen Sie das Untermenü Characteristics -> Minimum Stability Margins (Merkmale -> Minimale Stabilitätsreserven), um alle Übergangsfrequenzen und die zugehörigen Stabilitätsreserven anzuzeigen. Das resultierende Diagramm ist unten zu sehen.

Beachten Sie, dass es zwei 180-Grad-Phasenübergänge mit entsprechenden Amplitudenrändern von -9,35 dB und +10,6 dB gibt. Negative Amplitudenränder bedeuten, dass die Stabilität durch Verringern der Verstärkung verloren geht, während positive Amplitudenränder bedeuten, dass die Stabilität durch Erhöhen der Verstärkung verloren geht. Dies wird durch Plotten der Sprungantwort des geschlossenen Regelkreises für eine Verstärkungsabweichung von plus/minus 6 dB um k=1 bestätigt:
k1 = 2; T1 = feedback(G*k1,1); k2 = 1/2; T2 = feedback(G*k2,1); step(T,'b',T1,'r',T2,'g',12), legend('k = 1','k = 2','k = 0.5')

Das Diagramm zeigt verstärkte Oszillationen sowohl für kleinere als auch für größere Verstärkungswerte.
Sie können den Befehl allmargin verwenden, um alle Stabilitätsreserven zu berechnen. Beachten Sie, dass die Amplitudenränder als Verstärkungsverhältnisse und nicht in dB ausgedrückt werden. Verwenden Sie mag2db, um die Werte in dB zu konvertieren.
m = allmargin(G) GainMargins_dB = mag2db(m.GainMargin)
m =
struct with fields:
GainMargin: [0.3408 3.3920]
GMFrequency: [1.9421 16.4807]
PhaseMargin: 68.1140
PMFrequency: 7.0776
DelayMargin: 0.1680
DMFrequency: 7.0776
Stable: 1
GainMargins_dB =
-9.3510 10.6091
Siehe auch
margin | pole | diskmargin (Robust Control Toolbox)