stepinfo
Rise time, settling time, and other step-response characteristics
Syntax
Description
stepinfo lets you compute step-response characteristics
for a dynamic system model or for an array of step-response data. For a step response
y(t), stepinfo computes
characteristics relative to yinit and
yfinal, where
yinit is the initial offset, that is,
the value before the step is applied, and
yfinal is the steady-state value of the
response. These values depend on the syntax you use.
For a dynamic system model
sys,stepinfouses yinit = 0 and yfinal = steady-state value.For an array of step-response data
[y,t],stepinfouses yinit = 0 and yfinal = last sample value ofy, unless you explicitly specify these values.
For more information on how stepinfo computes the step-response
characteristics, see Algorithms.
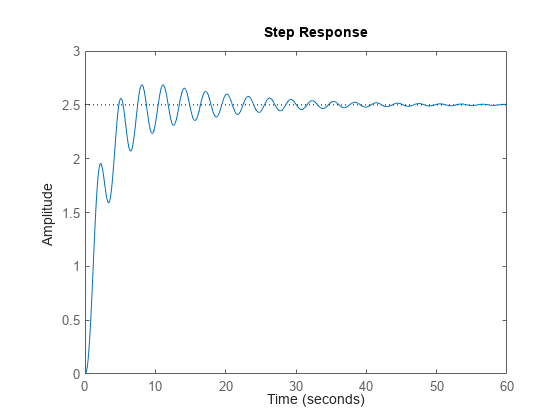
The following figure illustrates some of the characteristics
stepinfo computes for a step response. For this response, assume
that y(t) = 0 for t < 0, so
yinit = 0.

S = stepinfo(y,t)y and a corresponding time vector
t. For SISO system responses, y is
a vector with the same number of entries as t. For MIMO
response data, y is an array containing the responses of
each I/O channel. This syntax uses
yinit = 0 and the last value in
y (or the last value in each channel's corresponding
response data) as yfinal.
S = stepinfo(y,t,yfinal)yfinal. This syntax is useful when you know that the
expected steady-state system response differs from the last value in
y for reasons such as measurement noise. This syntax
uses yinit = 0.
For SISO responses, t and y are vectors
with the same length NS. For systems with
NU inputs and NY outputs, you can
specify y as an
NS-by-NY-by-NU
array (see step) and
yfinal as an
NY-by-NU array.
stepinfo then returns a
NY-by-NU structure array
S of response characteristics corresponding to each I/O
pair.
S = stepinfo(y,t,yfinal,yinit)yinit. This syntax is useful when your
y data has an initial offset; that is,
y is nonzero before the step occurs.
For SISO responses, t and y are vectors
with the same length NS. For systems with
NU inputs and NY outputs, you can
specify y as an
NS-by-NY-by-NU
array and yinit as an
NY-by-NU array.
stepinfo then returns a
NY-by-NU structure array
S of response characteristics corresponding to each I/O
pair.
S = stepinfo(___,'RiseTimeLimits',RT)RT
= [0.1 0.9]). The upper threshold RT(2) is also
used to calculate SettlingMin and
SettlingMax. These values are the minimum and maximum
values of the response occurring after the response reaches the upper threshold.
You can use this syntax with any of the previous input-argument combinations.
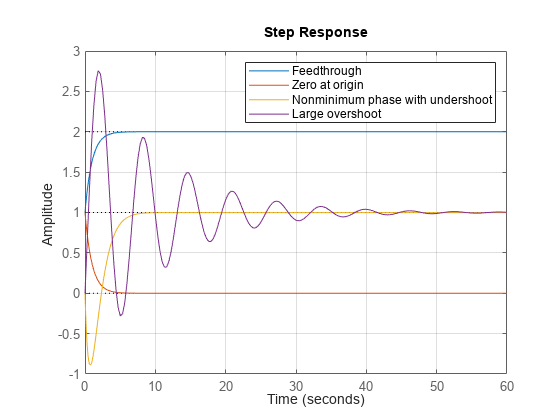
Examples
Input Arguments
Output Arguments
Algorithms
For a step response y(t),
stepinfo computes characteristics relative to
yinit and
yfinal. By default, for a dynamic
system model sys, stepinfo uses
yinit = 0 and
yfinal = steady-state value.
This table shows how stepinfo computes each
characteristic.
| Step-Response Characteristic | Description |
|---|---|
RiseTime | Time it takes for the response to rise from 10% to 90% of the way from yinit to yfinal |
TransientTime | The first time T such that the error |y(t) – yfinal| ≤ SettlingTimeThreshold × emax for t ≥ T, where emax is the maximum error |y(t) – yfinal| for t ≥ 0. By default, SettlingTimeThreshold = 0.02 (2% of the peak error). Transient time measures how quickly the transient dynamics die off. |
SettlingTime | The first time T such that the error |y(t) – yfinal| ≤ SettlingTimeThreshold × |yfinal – yinit| for t ≥ T. By
default, |
SettlingMin | Minimum value of y(t) once the response has risen |
SettlingMax | Maximum value of y(t) once the response has risen |
Overshoot | Percentage overshoot. Relative to the normalized response ynorm(t) = (y(t) – yinit)/(yfinal – yinit), the overshoot is the larger of zero and 100 × max(ynorm(t) – 1). |
Undershoot | Percentage undershoot. Relative to the normalized response ynorm(t), the undershoot is the smaller of zero and –100 × min(ynorm(t) ). |
Peak | Peak value of |y(t) – yinit| |
PeakTime | Time at which the peak value occurs |