Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

Ausgleich, Faltung und Hinzufügen eines zyklischen Präfixes

Schritt 3 von 5 in OFDM-Modulation mithilfe von MATLAB

In diesem Beispiel wird ein Frequenzbereichsausgleich eingefügt und gezeigt, wie eine kreisförmige Faltung in eine lineare Faltung konvertiert wird. Bei Betrachtung eines Linearkanalmodells ist das empfangene Signal die Faltung des übertragenen Signals mit der Kanalimpulsantwort. Im Frequenzbereich ist das empfangene Signal $\mathit{Y}\left(\mathit{f}\right)$ die lineare Faltung des übertragenen Signals $\mathit{U}\left(\mathit{f}\right)$ mit der Kanalimpulsantwort $\mathit{H}\left(\mathit{f}\right)$:

$\mathit{Y}\left(\mathit{f}\right)=\mathit{H}\left(\mathit{f}\right)\cdot \mathit{U}\left(\mathit{f}\right)$

Da OFDM-Empfänger den Frequenzbereichsausgleich verwenden, um das ursprünglich übertragene Signal wiederherzustellen, gilt:

$\mathit{U}\left(\mathit{f}\right)=\frac{\mathit{Y}\left(\mathit{f}\right)}{\mathit{H}\left(\mathit{f}\right)}$

Eine FFT-Verarbeitung ergibt die kreisförmige Faltung von u mit h. Damit die kreisförmige Faltung von u und h der linearen Faltung entspricht, müssen u und h mit Nullen auf eine Länge von mindestens (length(u) + length(h) - 1) aufgefüllt werden, bevor Sie die diskrete Fourier-Transformation (DFT) vornehmen können. Nachdem Sie das Produkt der DFTs invertiert haben, behalten Sie nur die ersten N + L - 1 Elemente bei. Ein Beispiel für diesen Prozess finden Sie unter dem Thema Linear and Circular Convolution.

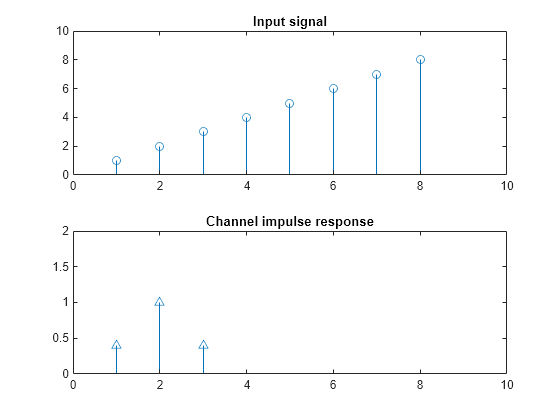
Definieren Sie ein kurzes Eingangssignal u1 und eine Kanalimpulsantwort h. Das Eingangssignal muss länger als die Kanalimpulsantwort sein. Zeigen Sie ein Stamm-Blatt-Diagramm der Signale an.

u1 = 1:8; 
h = [0.4 1 0.4];

figure
subplot(2,1,1)
stem(u1);
axis([0 10 0 10])
title("Input signal")
subplot(2,1,2)
stem(h);
axis([0 10 0 2])
title("Channel impulse response")

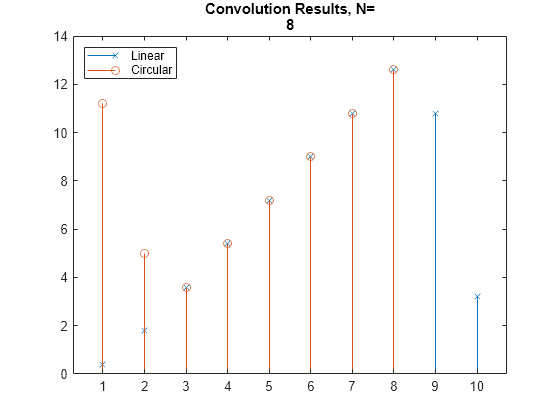
Vergleichen Sie die kreisförmige und die lineare Faltung von u1 mit h. Führen Sie mithilfe der Funktionen conv und cconv die lineare bzw. kreisförmige Faltung durch. Die Unschärfeeffekte aufgrund des nicht idealen Kanals führen dazu, dass die lineare und die kreisförmige Faltung an einigen Punkten unterschiedliche Ergebnisse liefern. Ein zyklisches Präfix (Cyclic Prefix, CP) ermöglicht die effektive Verwendung von OFDM in einem nicht idealen Kanal mit unbekannter Laufzeitverzögerung.

N = length(u1);
yl1 = conv(u1,h);
yc1 = cconv(u1,h,N);
figure;
stem(yl1,"x")
hold on;
stem(yc1,"o")
title(["Convolution Results - N=",int2str(N)])
legend ("Linear","Circular","Location","northwest")

Zyklisches Präfix (Cyclic Prefix, CP) hinzufügen

Bei der OFDM-Verarbeitung erfolgt das Auffüllen für die kreisförmige Faltung nicht durch Auffüllen der Signale mit Nullen, sondern durch Hinzufügen eines CP. Durch Hinzufügen eines CP, das die Endabtastungen des Symbols wiederholt, wird Folgendes möglich:

• Modellierung der linearen Faltung eines frequenzselektiven Mehrweg-Kanals als kreisförmige Faltung

• Verwendung einer FFT zum Berechnen der Faltung

• Einfache Frequenzbereichsverarbeitung für Kanalschätzung, -ausgleich und -synchronisation

• Wiederholte Abtastungen für deren Verwendung in Vorwärtsfehlerkorrekturschemas

L = length(h);      % Length of channel
N = length(u1);     % Length of input signal
ucp = u1(N-L+1:N);  % Use last samples of input signal as the CP
u2 = [ucp u1];      % Prepend the CP to the input signal
yl2 = conv(u2,h);   % Convolution of input+CP and channel
yl2 = yl2(L+1:end); % Remove CP to compare signals

figure;
stem(yc1,"x")
hold on;
stem(yl2,"o")
title("Convolution Results with Cyclic Prefix")
legend ("Linear","Circular","Location","northwest")

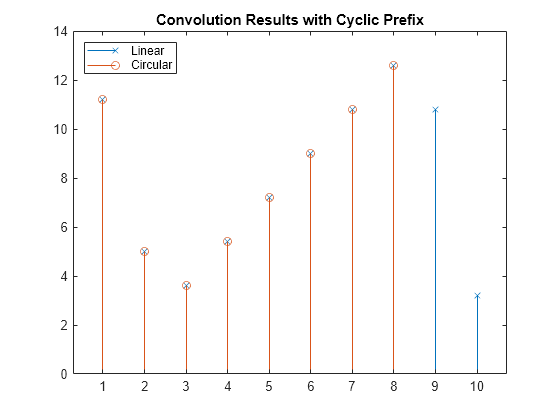
Vergleichen Sie die Folgen der linearen und der kreisförmigen Faltung.

if max(yc1 - yl2(1:N)) < 1e-8
    disp("Linear and circular convolution sequences match.")
else
    disp("Received symbols do not match transmitted symbols.")
end

Linear and circular convolution sequences match.

Siehe auch

Funktionen

• conv | cconv

Verwandte Themen

• OFDM-Modulation mithilfe von MATLAB
• Linear and Circular Convolution

Externe Websites

• Was ist OFDM? – MATLAB und Simulink

OFDM-Modulation mithilfe von MATLAB

Weiter