Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

Einführung in OFDM

Schritt 1 von 5 in OFDM-Modulation mithilfe von MATLAB

Das Multiplexing mit orthogonaler Frequenzteilung (Orthogonal Frequency Division Multiplexing, OFDM) ermöglicht Übertragungen mit hohen Datenübertragungsraten, indem modulierte Signalträger hoher Bandbreite auf viele modulierte Schmalband-Hilfsträger aufgeteilt werden. Bei OFDM-Übertragungen verringert die Verwendung von Schmalband-Hilfsträgern die Empfindlichkeit gegenüber dem frequenzselektiven Fading. Bei vielen der aktuellen drahtlosen und Telekommunikationsstandards wird die OFDM-Modulation mit mehreren Trägern verwendet. Die Unterstützung hoher Datenübertragungsraten in Systemen mit nur einem Träger erfordert einen Träger hoher Bandbreite und damit kurze Symboldauern. Beim Filtern eines Trägers hoher Bandbreite durch einen frequenzselektiven Mehrweg-Kanal wird die Signalgüte beträchtlich vermindert, da sich die Kanalimpulsantwort zeitlich über mehrere Symbole erstreckt. Außerdem wird die Anfälligkeit des Signals für das Symbolübersprechen (InterSymbol Interference, ISI) erhöht.

Diese Zeit- und Frequenzbereichsdiagramme zeigen ein hochfrequentes Signal, ein niederfrequentes Signal und die Antwort eines frequenzselektiven Mehrweg-Kanals. Wie das Zeitbereichsdiagramm zeigt, passt die Kanalimpulsantwort problemlos in genau ein Symbol des niederfrequenten Signals, erstreckt sich aber über mehrere Symbole des hochfrequenten Signals. Wie das Frequenzbereichsdiagramm zeigt, ist die Kanalstärke im gesamten Durchlassband des niederfrequenten Signals sehr flach, schwankt aber im gesamten Durchlassband des hochfrequenten Signals beträchtlich und verursacht ISI.

sa = helperPlotMultipath;

Um ISI beim Übertragen vieler paralleler Signale niedriger Bandbreite zu vermeiden, müssen die einzelnen Hilfsträger senkrecht zueinander („orthogonal“) stehen. Das Vermeiden von ISI beim Übertragen vieler orthogonaler Hilfsträger niedriger Bandbreite ist das Ziel von OFDM. Ein OFDM-Modulator konvertiert einen hochfrequenten seriellen Strom aus Symbolen in viele parallele niederfrequente Ströme. Jeder orthogonale hochfrequente Strom durchläuft einen relativ flachen Kanal mit minimalem ISI und kann problemlos entzerrt werden.

Zur Veranschaulichung betrachten Sie einen Impuls der Dauer ${\mathit{T}}_{\mathrm{sym}}=0.25\sec$, eine Symboldatenrate von ${\mathit{R}}_{\mathrm{sym}}=1/{\mathit{T}}_{\mathrm{sym}}=8\mathrm{Hz}$ und zusätzliche Impulse nach der Frequenzumsetzung um den Faktor ${\mathit{R}}_{\mathrm{sym}}$, 2${\mathit{R}}_{\mathrm{sym}}$ und 3${\mathit{R}}_{\mathrm{sym}}$. Die Impulse nach der Frequenzumsetzung werden als Hilfsträger bezeichnet. Diese Diagramme zeigen die Hilfsträger im Zeit- und im Frequenzbereich.

helperPlotOFDM

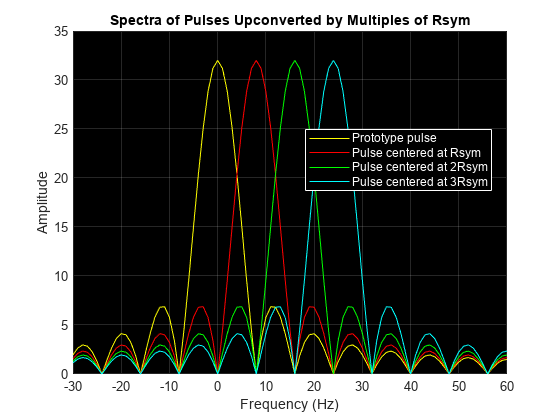
Das Frequenzbereichsdiagramm zeigt die orthogonalen Impulse nach der Frequenzumsetzung mit den Spektralspitzen jedes Hilfsträgers an den Nulldurchgängen aller anderen Impulse.

Ein OFDM-Modulator summiert alle diese Hilfsträger und bildet daraus das Ausgangssignal. Hier wurde auf die Hilfsträger die Basisband-Modulation mit der QAM-Methode angewendet. Mathematisch ergibt sich das abgetastete Modulator-Ausgangssignal $\mathit{s}\left(\mathit{k}\right)$ aus

$$\mathit{s}\left(\mathit{k}\right)=\sum _{\mathit{m}=0}^{\mathit{N}-1}{\mathit{a}}_{\mathit{m},\mathit{n}}{\mathit{e}}^{\mathrm{j2}\pi \mathit{m}{\mathit{R}}_{\mathrm{sym}}\mathit{k}\left(\frac{{\mathit{T}}_{\mathrm{sym}}}{\mathit{N}}\right)},$$

Dabei gilt:

• ${\mathit{a}}_{\mathit{m},\mathit{n}}$ ist ein QAM-moduliertes Symbol des $\mathit{m}$. Hilfsträgers im $\mathit{n}$. OFDM-Zeitsymbol

• ${\mathit{R}}_{\mathrm{sym}}$ ist die Symbolrate jedes der niederfrequenten QAM-Ströme

• ${\mathit{T}}_{\mathrm{sym}}=1/{\mathit{R}}_{\mathrm{sym}}$

• $\mathit{N}$ ist die Anzahl der Hilfsträger bzw. niederfrequenten QAM-Ströme

Diese Gleichung lässt sich zu

$$\mathit{s}\left(\mathit{k}\right)=\sum _{\mathit{m}=0}^{\mathit{N}-1}{\mathit{a}}_{\mathit{m},\mathit{n}}{\mathit{e}}^{\mathrm{j2}\pi \left(\frac{\mathit{m}\mathit{k}}{\mathit{N}}\right)},$$

vereinfachen. Dies ist eine skalierte Version der inversen diskreten Fourier-Transformation (Inverse Discrete Fourier Transform, IDFT) des QAM-Symbolstroms ${\mathit{a}}_{\mathit{m},\mathit{n}}$.

Siehe auch

Funktionen

• fft | ifft | ofdmmod | ofdmdemod | nrOFDMModulate (5G Toolbox) | nrOFDMDemodulate (5G Toolbox) | lteOFDMModulate (LTE Toolbox) | lteOFDMDemodulate (LTE Toolbox) | wlanWaveformGenerator (WLAN Toolbox)

Apps

• Wireless Waveform Generator

Verwandte Themen

• OFDM-Modulation mithilfe von MATLAB

Externe Websites

• Was ist OFDM? – MATLAB und Simulink

OFDM-Modulation mithilfe von MATLAB

Weiter