ROC Curves | Applied Machine Learning, Part 2
From the series: Applied Machine Learning
Use ROC curves to assess classification models. ROC curves plot the true positive rate vs. the false positive rate for different values of a threshold.
This video walks through several examples that illustrate broadly what ROC curves are and why you’d use them. It also outlines interesting scenarios you may encounter when using ROC curves.
Published: 18 Jan 2019
ROC curves are an important tool for assessing classification models. They're also a bit abstract, so let's start by reviewing some simpler ways to assess models.
Let's use an example that has to do with the sounds a heart makes. Given 71 different features from an audio recording of a heart, we try to classify if the heart sounds normal or abnormal.
One of the easiest metrics to understand is the accuracy of a model – or, in other words, how often it is correct. The accuracy is useful because it’s a single number, making comparisons easy. The classifier I’m looking at right now has an accuracy of 86.3%.
What the accuracy doesn’t tell you is how the model was right or wrong. For that, there’s the confusion matrix, which shows things such as the true positive rate. In this case, it is 74 %, meaning the classifier correctly predicted abnormal heart sounds 74% of the time. We also have the false positive rate of 9%. This is the rate at which the classifier predicted abnormal when the heart sound was actually normal.
The confusion matrix gives results for a single model. But most machine learning models don’t just classify things, they actually calculate probabilities. The confusion matrix for this model shows the result of classifying anything with a probability of >=0.5 as abnormal, and anything with probability <0.5 as normal. But that 0.5 doesn’t have to be fixed, and in fact we could threshold anywhere in the range of probabilities between 0 and 1.
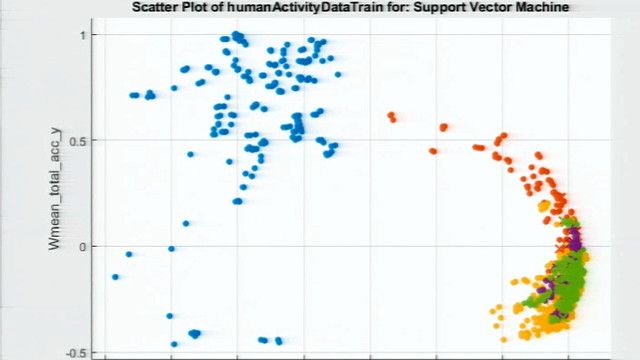
That’s where ROC curves come in. The ROC curve plots the true positive rate vs. the false positive rate for different values of this threshold.
Let’s look at this in more detail.
Here’s my model, and I’ll run it on my test data to get the probability of an abnormal heart sound. Now let’s start by thresholding these probabilities at 0.5. If I do that, I get a true positive rate of 74% and a false positive rate of 9%.
But what if we wanted to be very conservative, so even if the probability of a heart sound being abnormal was just 10%, we would classify it as abnormal.
If we do that, we get this point.
What if we wanted to be really certain, and only classify sounds with a 90% probability as being abnormal? Then we’d get this point, which has a much lower false positive rate, but also a lower true positive rate.
Now, if we were to create a bunch of values for this threshold in-between 0 and 1, say 1000 trials evenly spaced, we would get lots of these ROC points, and that’s where we get the ROC curve from. The ROC curve shows us the tradeoff in the true positive rate and false positive rate for varying values of that threshold.
There will always be a point on the ROC curve at 0 comma 0. In our case, everything is classified as “normal”. And there will always be a point at 1 comma 1, where everything is classified as “abnormal”.
The area under the curve is a metric for how good our classifier is. A perfect classifier would have an AUC of 1. In this example, the AUC is 0.926.
In MATLAB, you don’t need to do all of this by hand like I’ve done here. You can get the ROC curve and the AUC from the perfcurve function.
Now that we have that down, let’s look at some interesting cases for an ROC curve:
· If a curve is all the way up and to the left, you have a classifier that for some threshold perfectly labeled every point in the test data, and your AUC is 1. You either have a really good classifier, or you may want to be concerned that you don’t have enough data or that your classifier is overfit.
· If a curve is a straight line from the bottom left to the top right, you have a classifier that does no better than a random guess (its AUC is 0.5). You may want to try some other types of models or go back to your training data to see if you can engineer some better features.
· If a curve looks kind of jagged, that is sometimes due to the behavior of different types of classifiers. For example, a decision tree only has a finite number of decision nodes, and each of those nodes has a specific probability. The jaggedness comes from when the threshold value we talked about earlier crosses the probability at one of the nodes. Jaggedness also commonly comes from gaps in the test data.
As you can see from these examples, ROC curves can be a simple, yet nuanced tool for assessing classifier performance.
If you want to learn more about machine learning model assessment, check out the links in the description below.