Hauptinhalt
Results for
At the present time, the following problems are known in MATLAB Answers itself:
- Symbolic output is not displaying. The work-around is to disp(char(EXPRESSION)) or pretty(EXPRESSION)
- Symbolic preferences are sometimes set to non-defaults
- files get attached as .html and cannot be read from Answers
Hello, MATLAB fans!
For years, many of you have expressed interest in getting your hands on some cool MathWorks merchandise. I'm thrilled to announce that the wait is over—the MathWorks Merch Shop is officially open!

In our shop, you'll find a variety of exciting items, including baseball caps, mugs, T-shirts, and YETI bottles.
Visit the shop today and explore all the fantastic merchandise we have to offer. Happy shopping!
I was curious to startup your new AI Chat playground.
The first screen that popped up made the statement:
"Please keep in mind that AI sometimes writes code and text that seems accurate, but isnt"
Can someone elaborate on what exactly this means with respect to your AI Chat playground integration with the Matlab tools?
Are there any accuracy metrics for this integration?
Just shared an amazing YouTube video that demonstrates a real-time PID position control system using MATLAB and Arduino.
I don't like the change
16%
I really don't like the change
29%
I'm okay with the change
24%
I love the change
11%
I'm indifferent
11%
I want both the web & help browser
11%
38 Stimmen
We are thrilled to announce the grand prize winners of our MATLAB Shorts Mini Hack contest! This year, we invited the MATLAB Graphics and Charting team, the authors of the MATLAB functions used in every entry, to be our judges. After careful consideration, they have selected the top three winners:
Judge comments: Realism & detailed comments; wowed us with Manta Ray
2nd place – Jenny Bosten
Judge comments: Topical hacks : Auroras & Wind turbine; beautiful landscapes & nightscapes
3rd place - Vasilis Bellos
Judge comments: Nice algorithms & extra comments; can’t go wrong with Pumpkins
Judge comments: Impressive spring & cubes!
In addition, after validating the votes, we are pleased to announce the top 10 participants on the leaderboard:
Congratulations to all! Your creativity and skills have inspired many of us to explore and learn new skills, and make this contest a big success!

You can make a lot of interesting objects with matlab primitive shapes (e.g. "cylinder," "sphere," "ellipsoid") by beginning with some of the built-in Matlab primitives and simply applying deformations. The gif above demonstrates how the Manta animation was created using a cylinder as the primitive and successively applying deformations: (https://www.mathworks.com/matlabcentral/communitycontests/contests/8/entries/16252);
Similarly, last year a sphere was deformed to create a face in two of my submissions, for example, the profile in "waking":

You can piece-wise assemble images, but one of the advantages of creating objects with deformations is that you have a parametric representation of the surface. Creating a higher or lower polygon rendering of the surface is as simple as declaring the number of faces in the orignal primitive. For example here is the scene in "snowfall" using sphere with different numbers of input faces:
sphere(100)

sphere(500)

High poly models aren't always better. Low-polygon shapes can sometimes add a little distance from that low point in the uncanny valley.
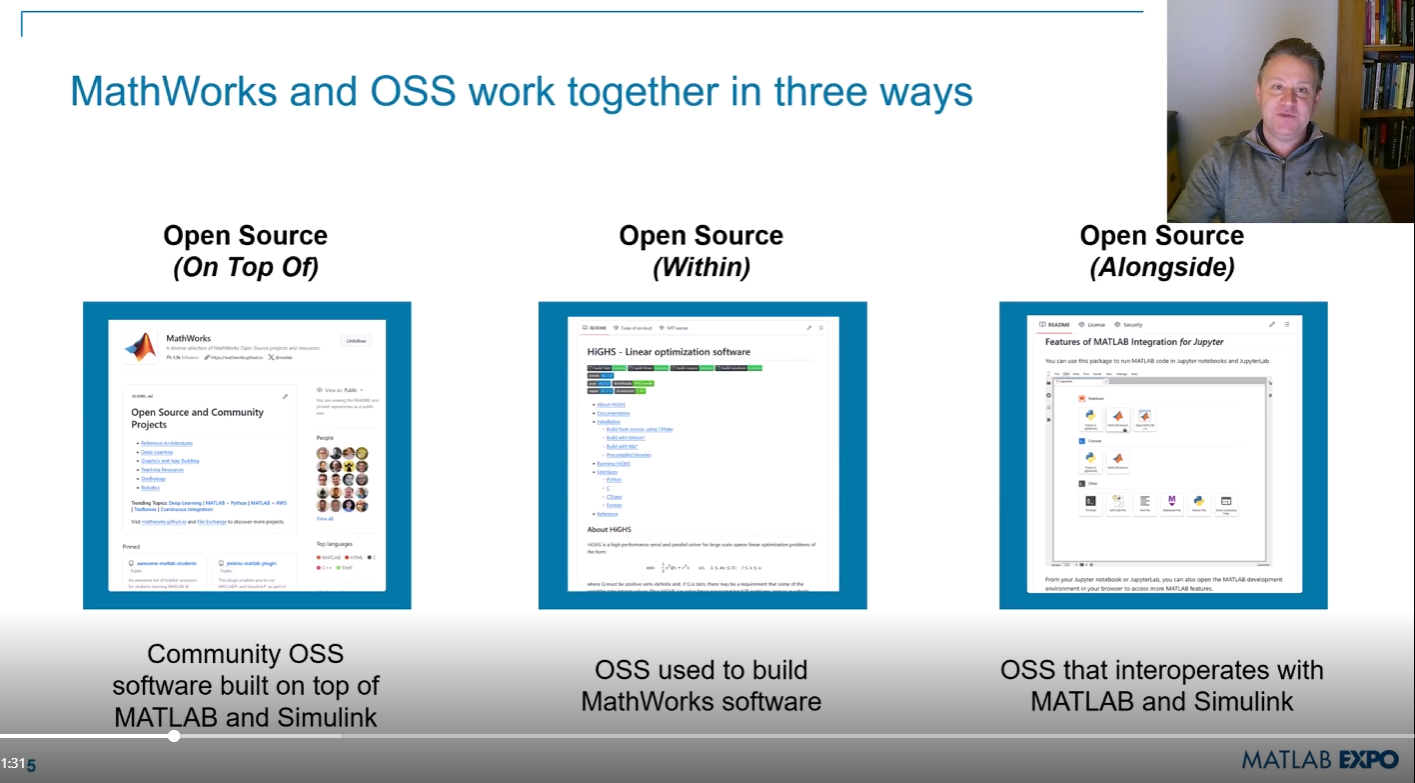
Next week is MATLAB EXPO week and it will be the first one that I'm presenting at! I'll be giving two presentations, both of which are related to the intersection of MATLAB and open source software.
- Open Source Software and MATLAB: Principles, Practices, and Python Along with MathWorks' Heather Gorr. We we discuss three different types of open source software with repsect to their relationship to MATLAB
- The CLASSIX Story: Developing the Same Algorithm in MATLAB and Python Simultaneously A collaboration with Prof. Stefan Guettel from University of Manchester. Developing his clustering algorithm, CLASSIX, in both Python and MATLAB simulatenously helped provide insights that made the final code better than if just one language was used.
There are a ton of other great talks too. Come join us! (It's free!) MATLAB EXPO 2024
Hi MATLAB Central community! 👋
I’m currently working on a project where I’m integrating MATLAB analytics into a mobile app, mainly to handle data-heavy tasks like processing sensor data and running predictive models. The app is built for Android, and while it’s not entirely MATLAB-based, I use MATLAB for a lot of data preprocessing and model training.
I wanted to reach out and see if anyone else here has experience with using MATLAB for similar mobile or embedded applications. Here are a few areas I’m focusing on:1. Optimizing MATLAB Code for Mobile Compatibility
I’ve found that some MATLAB functions work perfectly on desktop but may run slower or encounter limitations on mobile. I’ve tried using code generation and reducing function calls where possible, but I’m curious if anyone has other tips for optimizing MATLAB code for mobile environments?
2. Using MATLAB for Sensor Data Processing
I’m working with accelerometer and GPS data, and MATLAB has been great for preprocessing. However, I wonder if anyone has suggestions for handling large sensor datasets efficiently in MATLAB, especially if you've managed data in mobile contexts?
3. Integrating MATLAB Models into Mobile Apps
I’ve heard about using MATLAB Compiler SDK to integrate MATLAB algorithms into other environments. For those who have done this, what’s the best way to maintain performance without excessive computational strain on the device?
4. Data Visualization Tips
Has anyone had experience with mobile-friendly data visualizations using MATLAB? I’ve been using basic plots, but I’d love to know if there are any resources or toolboxes that make it easier to create lightweight, interactive visuals for mobile.
If anyone here has tips, tools, or experiences with MATLAB in mobile development, I’d love to hear them! Thanks in advance for any advice you can share!
Dear MATLAB contest enthusiasts,
Welcome to the third installment of our interview series with top contest participants! This time we had the pleasure of talking to our all-time rock star – @Jenny Bosten. Every one of her entries is a masterpiece, demonstrating a deep understanding of the relationship between mathematics and aesthetics. Even Cleve Moler, the original author of MATLAB, is impressed and wrote in his blog: "Her code for Time Lapse of Lake View to the West shows she is also a wizard of coordinate systems and color maps."
you to read it to learn more about Jenny’s journey, her creative process, and her favorite entries.
Question: Who would you like to see featured in our next interview? Let us know your thoughts in the comments!
It would be nice to have a function to shade between two curves. This is a common question asked on Answers and there are some File Exchange entries on it but it's such a common thing to want to do I think there should be a built in function for it. I'm thinking of something like
plotsWithShading(x1, y1, 'r-', x2, y2, 'b-', 'ShadingColor', [.7, .5, .3], 'Opacity', 0.5);
So we can specify the coordinates of the two curves, and the shading color to be used, and its opacity, and it would shade the region between the two curves where the x ranges overlap. Other options should also be accepted, like line with, line style, markers or not, etc. Perhaps all those options could be put into a structure as fields, like
plotsWithShading(x1, y1, options1, x2, y2, options2, 'ShadingColor', [.7, .5, .3], 'Opacity', 0.5);
the shading options could also (optionally) be a structure. I know it can be done with a series of other functions like patch or fill, but it's kind of tricky and not obvious as we can see from the number of questions about how to do it.
Does anyone else think this would be a convenient function to add?
My favorite image processing book is The Image Processing Handbook by John Russ. It shows a wide variety of examples of algorithms from a wide variety of image sources and techniques. It's light on math so it's easy to read. You can find both hardcover and eBooks on Amazon.com Image Processing Handbook
There is also a Book by Steve Eddins, former leader of the image processing team at Mathworks. Has MATLAB code with it. Digital Image Processing Using MATLAB
You might also want to look at the free online book http://szeliski.org/Book/
Over the past 4 weeks, 250+ creative short movies have been crafted. We had a lot of fun and, more importantly, learned new skills from each other! Now it’s time to announce week 4 winners.
Nature:
3D:
Seamless loop:
Holiday:
Fractal:
Congratulations! Each of you won your choice of a T-shirt, a hat, or a coffee mug. We will contact you after the contest ends.
Weekly Special Prizes
Thank you for sharing your tips & tricks with the community. These great technical articles will benefit community users for many years. You won a limited-edition pair of MATLAB Shorts!

In week 5, let’s take a moment to sit back, explore all of the interesting entries, and cast your votes. Reflect what you have learned or which entries you like most. Share anything in our Discussions area! There is still time to win our limited-edition MATLAB Shorts.
Go to this page, scroll down to the middle of the long page where you see "Coding Photo editing STEM Business ...." and select "STEM". Voilà!
In the past two years, large language models have brought us significant changes, leading to the emergence of programming tools such as GitHub Copilot, Tabnine, Kite, CodeGPT, Replit, Cursor, and many others. Most of these tools support code writing by providing auto-completion, prompts, and suggestions, and they can be easily integrated with various IDEs.
As far as I know, aside from the MATLAB-VSCode/MatGPT plugin, MATLAB lacks such AI assistant plugins for its native MATLAB-Desktop, although it can leverage other third-party plugins for intelligent programming assistance. There is hope for a native tool of this kind to be built-in.
Mini Hack is brilliant!Let's use MATLAB to create the future!
Pumpkins have been a popular, recurring, and ever-evolving theme in MATLAB during the past few years, and particularly during this time of year. Much of this is driven by the epic work of @Eric Ludlam and expanded upon by many others. The list of material is too extensive to go through everything individually, but I'm listing some of my favourite resources below and I highly recommend these to everyone as they're a lot of fun to play with:
Pumpkins are also particularly prominent during the yearly Mini Hack Contests. This year, I have jumped onto the bandwagon myself with my Floating Pumpkins entry:

In this post, I would like to introduce the concept of masking 3D surfaces in a festive and fun way, by showcasing how to apply it for carving faces on pumpkins step by step.
Let's start by drawing the pumpkin's body. The following was adapted from Eric's code:
n = 600; % Number of faces
% Shape pumpkin's rind (skin)
[X,Y,Z] = sphere(n);
% Shape pumpkin's ribs (ridges)
R = (1-(1-mod(0:20/n:20,2)).^2/12);
X = X.*R; Y = Y.*R; Z = Z.*R;
Z = (.8+(0-linspace(1,-1,n+1)'.^4)*.3).*Z;
function plotPumpkin(X,Y,Z)
figure
surf(X,Y,Z,'FaceColor',[1 .4 .1],'EdgeColor','none');
hold on
box on
axis([-1 1 -1 1 -1 1],'square')
xlabel('x'); xticks(-1:0.5:1)
ylabel('y'); yticks(-1:0.5:1)
zlabel('z'); zticks(-1:0.5:1)
material([.45,.7,.25])
camlight('headlight')
camlight('headlight')
lighting gouraud
end
plotPumpkin(X,Y,Z)
The next step is drawing the face for the mask. This can be done in 2D and can consist of any number of lines that form polygonal closed shapes and are appropriately scaled relative to the coordinates of the pumpkin. A quick example:
% Mouth
xm = [-.5:.1:.5 flip(-.5:.1:.5)];
ym = [.15 -.3 -.25 -.5 -.4 -.6 flip([.15 -.3 -.25 -.5 -.4]) .15 -.05 0 -.25 -.15 -.3 flip([.15 -.05 0 -.25 -.15])];
% Right eye
xr = [-.35 -.05 -.35];
yr = [.1 0 .5];
% Left eye
xl = abs(xr);
yl = yr;
figure('Color','w')
set(gcf,'Position',get(gcf,'Position')/2)
axes('Visible','off','NextPlot','Add')
axis tight square
fill(xm,ym,'k')
fill(xr,yr,'k')
fill(xl,yl,'k')
We then need to apply the 2D mask to the 3D surface. To do that, we project it onto the intersections of the surface with the XY plane. However, as we need the face to appear on the side of the pumpkin, we first need to rotate the pumpkin so that the front side is facing upwards. Essentially, we need to rotate the pumpkin around the x-axis by -π/2 rad.
Let's do this from first principles to better understand the process:
theta = [-pi/2,0,0];
[X,Y,Z] = xyzRotate(X,Y,Z,theta);
function [X,Y,Z] = xyzRotate(X,Y,Z,theta)
% Rotation matrices
Rx = [1 0 0;0 cos(theta(1)) -sin(theta(1));0 sin(theta(1)) cos(theta(1))];
Ry = [cos(theta(2)) 0 sin(theta(2));0 1 0;-sin(theta(2)) 0 cos(theta(2))];
Rz = [cos(theta(3)) -sin(theta(3)) 0;sin(theta(3)) cos(theta(3)) 0;0 0 1];
for i=1:size(X,1)
for j=1:size(X,2)
r=Rx*Ry*Rz*[X(i,j);Y(i,j);Z(i,j)];
X(i,j)=r(1);
Y(i,j)=r(2);
Z(i,j)=r(3);
end
end
end
More information about these transformations can be found here:
When plotting we get:
plotPumpkin(X,Y,Z)
Note that as we have only rotated this around the x-axis, Ry and Rz are equal to eye(3).
We can now apply the mask as discussed. We do this by using one of my favourite functions inpolygon. This gives us the corresponding indices of all the data points located inside our polygonal regions. At this stage, it's important to keep the following in mind:
- The number of faces (n) controls the discretization of the pumpkin. The larger it is, the smoother the mask will be, but at the same time the computational cost will also increase. If you are using this for the contest which has a timeout limit of 235 seconds, you might need to adjust it accordingly.
- You will also need to restrict the Z-coordinates appropriately (Z>=0) so that the mask is only applied on the front side of the pumpkin.
- If you are animating the face mask (more information about this below), and you need the eyes and mouth to fully close at any point, avoid using the second argument of the inpolygon function that gives you the points located on the edge of the regions.
The masking function is given below:
function [X,Y,Z] = Mask(X,Y,Z,xm,ym,xr,yr,xl,yl)
mask = ones(size(Z));
mask((inpolygon(X,Y,xm,ym)|inpolygon(X,Y,xr,yr)|inpolygon(X,Y,xl,yl))&Z>=0) = NaN;
Z = Z.*mask;
end
Applying the mask gives us:
[X,Y,Z]=Mask(X,Y,Z,xm,ym,xr,yr,xl,yl);
plotPumpkin(X,Y,Z)
arrayfun(@(x)light('style','local','position',[0 0 0],'color','y'),1:2)
We can see that MATLAB was thoughtful enough to automatically remove the pulp from inside the pumpkin, proving its convenience time and time again.
We can then rotate the pumpkin back and add the stem to get the final result:
theta = [pi/2,0,0];
[X,Y,Z] = xyzRotate(X,Y,Z,theta);
% Stem
s = [1.5 1 repelem(.7, 6)] .* [repmat([.1 .06],1,round(n/20)) .1]';
[t,p] = meshgrid(0:pi/15:pi/2,linspace(0,pi,round(n/10)+1));
Xs = repmat(-(.4-cos(p).*s).*cos(t)+.4,2,1);
Ys = [-sin(p).*s;sin(p).*s];
Zs = repmat((.5-cos(p).*s).*sin(t)+.55,2,1);
plotPumpkin(X,Y,Z)
arrayfun(@(x)light('style','local','position',[0 0 0],'color','y'),1:2)
surf(Xs,Ys,Zs,'FaceColor','#008000','EdgeColor','none');
And that's it. You can now add some change to the mask's coordinates between frames and play around with the lighting to get results such as these (more information on how to do this on my Teaser entry):


I hope you have found this tutorial useful, and I'm looking forward to seeing many more creative entries during the final week of the contest.
What incredible short movies can be crafted with no more than 2000 characters of MATLAB code? Discover the creativity in our GALLERY from the MATLAB Shorts Mini Hack contest.
Vote on your favorite short movies by Nov.10th. We are giving out MATLAB T-shirts to 10 lucky voters!

Tips: the more you vote, the higher your chance to win.
At the onset of each week, I release a post that analyzes code with the intent of making it accessible for beginners, while also providing insights that can benefit more experienced users seeking to learn new techniques or approaches.
This week, my inspiration comes from the fractal art produced in MATLAB, as presented in my entry Whispers of the Ocean's Breeze:

Below, I offer a pretty detailed walkthrough of the code break-down, with the goal of creating both an educational and stimulating experience for those eager to learn or find some inspiration. Taking into account that this post is somewhat lengthy, it provides a breakdown and summary of various techniques. It is my hope that it will assist someone and allow readers to focus on the sections that are of most interest to them.
While the code contains comments, this post offers additional explanations and details.
1. Function Definition and Metadata
function drawframe(f)
Line 1: Defines the main function drawframe, which takes a single parameter f. This parameter controls various aspects of the animation, such as movement or speed.
% Audio source: Klapa Šibenik (comp. Arsen Dedić) -
% - Zaludu me svitovala mati
% (Hrvatska 🇭🇷, (Dalmacija))
% Enhanced aesthetics and added dynamic movement,
% offering a creative Remix of my earlier concept.
% (This version brings richer visual appeal,smoother transitions,
% and a more engaging animation flow)
Lines 2-4: Commented-out lines providing metadata or notes about the code. These comments describe the aesthetic goals and improvements in this version, highlighting that it's a remix of one of my earlier entry's, with added dynamic movement and smoother visuals. (These notes are not executed by MATLAB.)
A general tip for using comments: include comments in your code as frequently as needed. They serve as helpful reminders of what each part of the code does, especially when you revisit it after some time, and make it easier for others who may read or use your code.
2. Function Call to seaweed
seaweed(4) % The value in brackets can be adjusted for significantly
% enhanced visualization,
% but it exceeds the 235-second limit in the contest script.
% Feel free to experiment at Desktop workstation - with higher
% values in the loop,
% for more complex and beautiful results.
Line 5: Calls the seaweed function with an argument of 4. The number 4 controls the recursion depth, affecting how detailed or complex the 'seaweed' pattern will be.
Lines 6-9: Comment explaining that increasing the value in seaweed(4) enhances visualization but may exceed time limits in contest environment(s). This suggests adjusting this parameter on a desktop to explore more intricate patterns...
3. Definition of seaweed Function
function seaweed(k)
% Set up the figure window with a specific position and background color
figure('Position', [60+2*f, 60-2*f, 600, 600], 'Color', [0.15, 0.15, 0.5]);
Line 10: Defines the seaweed function, which takes a parameter k (depth of recursion). This function initializes the graphical figure window.
Line 12: Sets up the figure window with a position influenced by f, making the figure’s position change dynamically with f. The background color [0.15, 0.15, 0.5] creates a dark blue background, enhancing the underwater aesthetic.
4. Recursive Drawing with crta Function
crta([0, 0], 90, k, k);
% Make the axes equal and turn them off for a clean figure
axis equal
axis off
Line 14: Calls the recursive function crta, starting the drawing process at [0, 0](origin point) with a 90-degree angle. Both k values set the initial recursion depth and maximum recursion level.
Lines 16-17: Sets the axis scale to equal, ensuring no distortion, and turns off the axes for a cleaner display.
5. Definition of crtaFunction and Initialization of Parameters
function crta(tck, ugao, prstiter, r)
% Define thickness of line segment proportional to current depth
sir = 5 * (prstiter / r);
% Define length of the line segment
duz1 = 5 * prstiter;
Line 18: Defines crta, a nested function within seaweed, taking parameters tck (current coordinates), ugao (angle), prstiter (current recursion depth), and r (maximum recursion depth).
Lines 20-21: Defines sir (line thickness) to be proportional to the current recursion depth, prstiter, creating thinner branches as depth increases. While, duz1 defines the line segment length, which shortens with each recursion, creating perspective.
6. Angle Calculations for Branching
% Define four branching angles with slight variations
ug1 = ugao + 15 + (f / 15);
ug2 = ugao + 7 - f / 15;
ug3 = ugao - 7 + f / 15;
ug4 = ugao - 15 - f / 15;
Lines 23-27: Sets branching angles ug1, ug2, ug3, and ug4 relative to the initial angle ugao, adding and subtracting small amounts. These angles, influenced by f, introduce subtle variations, enhancing the natural appearance.
7. Calculations for Branch Endpoints
% Calculate endpoints of each line segment for the four angles
a1 = duz1 * sind(ug1) + tck(2);
b1 = duz1 * cosd(ug1) + tck(1);
c2 = duz1 * sind(ug2) + tck(2);
a2 = duz1 * cosd(ug2) + tck(1);
b3 = duz1 * sind(ug3) + tck(2);
c3 = duz1 * cosd(ug3) + tck(1);
d4 = duz1 * sind(ug4) + tck(2);
e4 = duz1 * cosd(ug4) + tck(1);
Lines 29-36: Calculates x and y endpoints for each of the four branches using sind and cosd functions, which convert angles into coordinates. Each branch starts at tck(current In this section, the code calculates the endpoints of four line segments, each corresponding to a distinct angle (ug1, ug2,ug3, and ug4). These endpoints are computed based on the length of the line segment duz1, which scales with recursion depth to make each segment shorter as the recursive function progresses. The trigonometric functions sind and cosd are used here to calculate the horizontal and vertical displacements of each segment relative to the current position, tck. While, sind and cosd functions compute the sine and cosine of each angle in degrees, returning the y and x displacements, respectively. For each angle, multiplying by duz1scales these displacements to achieve the intended length for each line segment. Each endpoint coordinate is calculated by adding these displacements to the initial position, tck, to determine the final position for each branch segment:
- a1 and b1 represent the y and x endpoints for the segment at angle ug1
- c2 and a2 represent the y and x endpoints for the segment at angle ug2
- b3 and c3 represent the y and x endpoints for the segment at angle ug3
- d4 and e4 represent the y and x endpoints for the segment at angle ug4
These coordinates form the four main branches radiating out from the current position in different directions. By varying the angle slightly for each branch and scaling the length proportionally, the function generates a visually rich, organic branching structure that resembles seaweed or other natural patterns.
8. Midpoint Calculations for Additional Complexity
% Calculate midpoints for additional "leaves" to
% simulate complexity
uga1 = ug2 - 5 + f / 5;
ugb2 = ug3 + 5 - f / 5;
uga2 = duz1 / 2 * sind(uga1) + c2 + f / 20;
ugb3 = duz1 / 2 * cosd(uga1) + a2 - f / 20;
ugc2 = duz1 / 2 * sind(ugb2) + b3 + f / 20;
ugda1 = duz1 / 2 * cosd(ugb2) + c3 - f / 20;
Lines 38-44: Calculates midpoint angles and positions for extra “leaf” structures. This further enhances the fractal appearance by adding more detail, as these points fall between main branches!
Additional midpoints are calculated to add further detail and complexity to the fractal pattern. These midpoints represent extra branches or “leaves” that emerge from within the main branch segments, enhancing the natural, organic appearance of the fractal structure. Consequently, uga1 and ugb2 are new angles derived by slightly modifying the main branch angles ug2and ug3. The adjustments are made by adding and subtracting small values, including a component based on f. These subtle variations create slight deviations in the angles of the additional branches, making them appear more random and organic, like leaves growing off main stems in varied directions. Once the new angles uga1 and ugb2 are defined, they are used to calculate intermediate coordinates along the main branch lines. These midpoints are positioned halfway along each branch segment, representing the location from which the extra “leaf” branches will emerge.
To find these midpoints:
- uga2 and ugb3 use sind(uga1) and cosd(uga1)to calculate the y and x coordinates halfway along the segment for angle ug2.
- ugc2 and ugda1 similarly use sind(ugb2) and cosd(ugb2) to get the coordinates for angle ug3.
Each midpoint calculation also includes a slight additional offset based on f (like f / 20), adding variation in their positions and contributing to the irregular, natural look of the structure.
By adding these secondary branches, the fractal pattern gains more intricacy. These “leaves” give a more complex and dense appearance, resembling the growth patterns of plants or seaweed where smaller branches diverge from main stems. The addition of midpoints also contributes to the overall depth and richness of the fractal design, ensuring that each recursive call doesn’t simply repeat but also grows in visual detail, making the resulting fractal more visually appealing and realistic. The midpoint calculations thus play a crucial role in enhancing the visual complexity of the fractal by introducing smaller, secondary branches that break up the regularity of the main branches, making the structure more detailed and lifelike.
9. Color Definition Based on Depth
% Define color based on depth, simulating a gradient effect
% as recursion deepens
boja = [1 - (prstiter / r), 1 - 0.5 * (prstiter / r), 0];
Line 46: Defines the color boja as a gradient that shifts from yellow to dark orange based on recursion depth. This gradient effect enhances the visual depth of the pattern.
This code sets up a color gradient for each branch segment based on its recursion depth. This approach not only adds aesthetic appeal but also visually separates different levels of recursion, making it easier to perceive depth within the fractal. The variable boja is an RGB color array, where each element represents the intensity of red, green, and blue respectively, on a scale from 0 (no intensity) to 1(full intensity).
The first element, 1 - (prstiter / r), controls the red component. The second element, 1 - 0.5 * (prstiter / r), controls the green component. The third element is set to 0, meaning there is no blue in the color, resulting in a gradient that shifts from yellow (where both red and green are high) to darker orange and then brownish tones as recursion deepens. The color gradually shifts from a bright yellowish tone at shallow recursion levels to a darker, warmer orange as recursion depth increases. This is achieved by gradually decreasing the red and green components of the color as prstiter (current recursion depth) approaches r (maximum recursion depth). At the top levels of recursion (where prstiter is closer to r), the color becomes darker and more subdued, giving the branches a gradient that makes the structure look natural and complex. This effect is reminiscent of how colors in nature tend to fade or darken with distance or depth, such as in underwater scenes where light penetration decreases with depth.
The gradient serves as a visual cue that helps distinguish between different recursion levels. Since each level is progressively darker, viewers can intuitively sense the depth of each branch, which adds to the three-dimensional effect of the fractal. The use of warm colors (yellow to orange) for each branch segment helps the fractal pattern stand out vividly against the cool blue background set in the seaweed function. This color contrast enhances the underwater, organic look of the structure, making it appear as though the "seaweed" is reaching out toward a light source above. This coloring strategy also contributes to the fractal’s aesthetic complexity. By associating color depth with recursion depth, the fractal appears to have layers, creating a visually satisfying and realistic effect.
10. Plotting Branch Segments
% Plot main branches from the starting point (tck) to the calculated
% endpoints with color and transparency
p1 = plot([tck(1), b1], [tck(2), a1], 'LineWidth', sir, 'Color', boja);
hold on
s2 = plot([tck(1), a2], [tck(2), c2], 'LineWidth', sir, 'Color', boja);
s3 = plot([tck(1), c3], [tck(2), b3], 'LineWidth', sir, 'Color', boja);
s4 = plot([tck(1), e4], [tck(2), d4], 'LineWidth', sir, 'Color', boja);
% Plot secondary branches connecting midpoints for added detail
s5 = plot([a2, ugb3], [c2, uga2], 'LineWidth', sir, 'Color', boja);
s6 = plot([c3, ugda1], [b3, ugc2], 'LineWidth', sir, 'Color', boja);
Lines 48-56: Plots the main branches and secondary branches for added detail. Each plot command connects points with a specified thickness and color, creating the branching effect.
Here presented code, plots the main branches and additional “leaf” segments, giving form to the fractal pattern. Each plot command specifies a line segment by connecting two points, with attributes like line width (sir) and color (boja) enhancing the realism and aesthetic detail. Lines from p1to s4 represent a branch extending outward from the current point tck to its calculated endpoint. The branch segments p1, s2, s3, and s4 form the primary structure of the fractal by branching off at angles ug1, ug2, ug3, and ug4 respectively, calculated in earlier presented and explained steps. The plot command takes a pair of [x, y] coordinates that define the line’s start and end points. For instance, p1 = plot([tck(1), b1], [tck(2), a1], 'LineWidth', sir, 'Color', boja); draws a line from tck(the current position) to (b1, a1), one of the endpoints.
The arguments 'LineWidth', sir and 'Color', boja ensure that each line segment has a thickness and color appropriate to its recursion level, making higher-level branches thicker and more prominent while creating a natural gradient. The command hold on is crucial here, it allows MATLAB to draw multiple line segments within the same figure window without erasing the previous segments. This is necessary for the recursive nature of the fractal, as each call to crtaadds branches to the existing structure, layering them to form a complex, interconnected pattern. Lines s5 and s6 represent additional “leaf”segments, plotted between midpoints calculated in Section 8. These smaller branches diverge from the main branches, adding further intricacy and detail to the fractal. By connecting midpoints (such as a2 to ugb3 and c3 to ugda1), the code generates extra “leafy” offshoots that break up the regularity of the main branches.
These segments make the fractal look more organic, akin to the smaller branches and leaves one might see on real plants or seaweed. Similar to the main branches, the secondary branches use sir and boja for line width and color, ensuring consistent visual depth and blending them seamlessly into the overall pattern. This layering allows the fractal to resemble natural structures like foliage or underwater vegetation. The combination of primary and secondary branches contributes to both symmetry and asymmetry in the fractal. While the primary branches provide a balanced, four-way split, the secondary branches introduce slight irregularities, which lend an organic feel to the pattern. Finally, by plotting each segment separately, the code achieves a highly customizable structure. Line thickness, color, and endpoint coordinates can be easily adjusted for each recursion level, allowing flexibility in the appearance and feel of the fractal.
11. Setting Transparency and Recursion
% Set transparency for each plot segment
s1.Color(4) = 0.95;
s2.Color(4) = 0.95;
s3.Color(4) = 0.95;
s4.Color(4) = 0.95;
s5.Color(4) = 0.95;
s6.Color(4) = 0.95;
% Continue recursive drawing if there are levels left ( prstiter > 0)
if prstiter - 1 > 0
% Recursive calls for each of the main branches with
% updated angles and decreased recursion depth
crta([b1, a1], ug1, prstiter - 1, r);
crta([ugb3, uga2], uga1, prstiter - 1, r);
crta([ugda1, ugc2], ugb2, prstiter - 1, r);
crta([e4, d4], ug4, prstiter - 1, r);
end
end
end
Lines 58-63: Sets the transparency of each branch segment to 0.95, creating a slightly translucent effect.
Lines 65-71: Checks if recursion should continue (i.e., if prstiter > 0). If so, the crta function recursively calls itself with updated angles and positions, generating the next level of branching until prstiter reaches the value of 0.
This code applies transparency to each branch segment to enhance the visual layering effect and initiates further recursion for drawing deeper levels of the fractal. Lines s1.Color(4) = 0.95; through s6.Color(4) = 0.95; apply transparency to each of the plot segments, allowing branches to be slightly see-through. In MATLAB, the fourth element of the Color property, Color(4), represents the alpha (transparency) value. That is, setting it to 0.95 makes each branch segment 95% opaque, meaning it is just translucent enough to create a layered effect where overlapping branches blend slightly. This subtle transparency creates depth, giving the impression that some branches are behind others, which enhances the natural, three-dimensional appearance of the fractal structure. The transparency effect also softens the overall image, making the fractal appear less rigid and more fluid in water.
Line: if prstiter - 1 > 0, checks if further recursion should occur by verifying that prstiter (the current recursion depth) is greater than 1. If prstiter is greater than 1, the function proceeds to recursively call crta, reducing prstiter by 1 with each call. This gradual reduction in prstiter ensures that recursion continues until the maximum depth, defined by r, is reached. As the recursion depth decreases with each call, the branch segments become progressively shorter and thinner, creating a tapered effect that adds to the realistic, fractal-like branching.
Recursive Calls of the function crta, calls itself four times, once for each main branch direction (ug1, ug2, ug3, ug4), using updated coordinates and angles:
- crta([b1, a1], ug1, prstiter - 1, r); initiates a recursive call for the branch at angle ug1.
- crta([ugb3, uga2], uga1, prstiter - 1, r); starts recursion from the midpoint branch at angle uga1.
- crta([ugda1, ugc2], ugb2, prstiter - 1, r); continues recursion from the midpoint branch at angle ugb2.
- crta([e4, d4], ug4, prstiter - 1, r); initiates recursion from the branch at angle ug4.
Each recursive call passes a new starting point (calculated in previous steps) and an adjusted angle. These recursive calls add the next level of branching, gradually building out the entire fractal structure. The recursive calls are fundamental to constructing the fractal pattern. By creating multiple levels of branching, each progressively smaller and more complex, the fractal develops a rich, layered structure that mimics natural growth patterns. The recursive structure also allows for variations in each level, as each branch is influenced by slightly different angles and positions, resulting in an organic, non-uniform look. This natural irregularity is key to creating a visually appealing fractal. Additionally, since each recursive call has transparency applied to its branches, the resulting fractal has a soft, blended appearance. Overlapping branches appear to merge gently, creating a cohesive, three-dimensional visual effect.
End of Code
end
This line closes the entire drawframe function, completing the recursive fractal drawing of the seaweed structure.
Sometimes, neglecting to include the necessary closure for a function can lead to unexpected surprises in the code. Always be vigilant about ensuring that functions, loops, and other structures are properly closed.

Summary: This whole code uses recursion and geometry to create natural-looking, fractal-inspired patterns that mimic the movement and appearance of seaweed, achieving complexity and organic flow through simple recursive structure and dynamic angle variations.





