Hauptinhalt
Ergebnisse für

Attaching the Photoshop file if you want to modify the caption.
Toolbox 全部入りの MATLAB ライセンス
67%
まだ持っていない Toolbox (下記にコメントください)
0%
MATLAB T シャツ
17%
MATLAB ルービックキューブ
0%
MATLAB 靴下
6%
MathWorks オフィス訪問チケット
11%
18 Stimmen
この場は MATLAB や Simulink を使っている皆さんが、気軽に質問や情報交換ができる場所として作られました。日本語でも気軽に投稿ができるように今回日本語チャネルを解説します。
ユーザーの皆様とのやり取りを通じて、みんなで知識や経験を共有し、一緒にスキルアップしていきましょう。 どうぞお気軽にご参加ください。
そして日本語チャネル開設にあたってコメントくださった皆様、ありがとうございます!

What better way to add a little holiday magic than the L-shaped membrane atop your evergreen? My colleagues output the shape and then added some thickness and an interior cylinder in Blender. Then, the shape was exported to STL and 3D printed (in several pieces). Then glued, sanded, primed, sanded again and painted. If you like, the STL file is attached. Thank you to https://blogs.mathworks.com/community/2013/06/20/paul-prints-the-l-shaped-membrane/ and a tip of the hat to MATLAB Ornament. Happy Holidays!


If you have a folder with an enormous number of files and want to use the uigetfile function to select specific files, you may have noticed a significant delay in displaying the file list.
Thanks to the assistance from MathWorks support, an interesting behavior was observed.
For example, if a folder such as Z:\Folder1\Folder2\data contains approximately 2 million files, and you attempt to use uigetfile to access files with a specific extension (e.g., *.ext), the following behavior occurs:
Method 1: This takes minutes to show me the list of all files
[FileName, PathName] = uigetfile('Z:\Folder1\Folder2\data\*.ext', 'File selection');
Method 2: This takes less than a second to display all files.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data');
Method 3: This method also takes minutes to display the file list. What is intertesting is that this method is the same as Method 2, except that a file seperator "\" is added at the end of the folder string.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data\');
I was informed that the Mathworks development team has been informed of this strange behaviour.
I am using 2023a, but think this should be the same for newer versions.
This post is more of a "tips and tricks" guide than a question.
If you have a folder with an enormous number of files and want to use the uigetfile function to select specific files, you may have noticed a significant delay in displaying the file list.
Thanks to the assistance from MathWorks support, an interesting behavior was observed.
For example, if a folder such as Z:\Folder1\Folder2\data contains approximately 2 million files, and you attempt to use uigetfile to access files with a specific extension (e.g., *.ext), the following behavior occurs:
Method 1: This takes minutes to show me the list of all files
[FileName, PathName] = uigetfile('Z:\Folder1\Folder2\data\*.ext', 'File selection');
Method 2: This takes less than a second to display all files.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data');
Method 3: This method also takes minutes to display the file list. What is intertesting is that this method is the same as Method 2, except that a file seperator "\" is added at the end of the folder string.
[FileName, PathName] = uigetfile('*.ext', 'File selection','Z:\Folder1\Folder2\data\');
I was informed that the Mathworks development team has been informed of this strange behaviour.
I am using 2023a, but think this should be the same for newer versions.


Christmas is coming, here are two dynamic Christmas tree drawing codes:
Crystal XMas Tree
function XmasTree2024_1
fig = figure('Units','normalized', 'Position',[.1,.1,.5,.8],...
'Color',[0,9,33]/255, 'UserData',40 + [60,65,75,72,0,59,64,57,74,0,63,59,57,0,1,6,45,75,61,74,28,57,76,57,1,1]);
axes('Parent',fig, 'Position',[0,-1/6,1,1+1/3], 'UserData',97 + [18,11,0,13,3,0,17,4,17],...
'XLim',[-1.5,1.5], 'YLim',[-1.5,1.5], 'ZLim',[-.2,3.8], 'DataAspectRatio', [1,1,1], 'NextPlot','add',...
'Projection','perspective', 'Color',[0,9,33]/255, 'XColor','none', 'YColor','none', 'ZColor','none')
%% Draw Christmas tree
F = [1,3,4;1,4,5;1,5,6;1,6,3;...
2,3,4;2,4,5;2,5,6;2,6,3];
dP = @(V) patch('Faces',F, 'Vertices',V, 'FaceColor',[0 71 177]./255,...
'FaceAlpha',rand(1).*0.2+0.1, 'EdgeColor',[0 71 177]./255.*0.8,...
'EdgeAlpha',0.6, 'LineWidth',0.5, 'EdgeLighting','gouraud', 'SpecularStrength',0.3);
r = .1; h = .8;
V0 = [0,0,0; 0,0,1; 0,r,h; r,0,h; 0,-r,h; -r,0,h];
% Rotation matrix
Rx = @(V, theta) V*[1 0 0; 0 cos(theta) sin(theta); 0 -sin(theta) cos(theta)];
Rz = @(V, theta) V*[cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0; 0 0 1];
N = 180; Vn = zeros(N, 3); eval(char(fig.UserData))
for i = 1:N
tV = Rz(Rx(V0.*(1.2 - .8.*i./N + rand(1).*.1./i^(1/5)), pi/3.*(1 - .6.*i./N)), i.*pi/8.1 + .001.*i.^2) + [0,0,.016.*i];
dP(tV); Vn(i,:) = tV(2,:);
end
scatter3(Vn(:,1).*1.02,Vn(:,2).*1.02,Vn(:,3).*1.01, 30, 'w', 'Marker','*', 'MarkerEdgeAlpha',.5)
%% Draw Star of Bethlehem
w = .3; R = .62; r = .4; T = (1/8:1/8:(2 - 1/8)).'.*pi;
V8 = [ 0, 0, w; 0, 0,-w;
1, 0, 0; 0, 1, 0; -1, 0, 0; 0,-1,0;
R, R, 0; -R, R, 0; -R,-R, 0; R,-R,0;
cos(T).*r, sin(T).*r, T.*0];
F8 = [1,3,25; 1,3,11; 2,3,25; 2,3,11; 1,7,11; 1,7,13; 2,7,11; 2,7,13;
1,4,13; 1,4,15; 2,4,13; 2,4,15; 1,8,15; 1,8,17; 2,8,15; 2,8,17;
1,5,17; 1,5,19; 2,5,17; 2,5,19; 1,9,19; 1,9,21; 2,9,19; 2,9,21;
1,6,21; 1,6,23; 2,6,21; 2,6,23; 1,10,23; 1,10,25; 2,10,23; 2,10,25];
V8 = Rx(V8.*.3, pi/2) + [0,0,3.5];
patch('Faces',F8, 'Vertices',V8, 'FaceColor',[255,223,153]./255,...
'EdgeColor',[255,223,153]./255, 'FaceAlpha', .2)
%% Draw snow
sXYZ = rand(200,3).*[4,4,5] - [2,2,0];
sHdl1 = plot3(sXYZ(1:90,1),sXYZ(1:90,2),sXYZ(1:90,3), '*', 'Color',[.8,.8,.8]);
sHdl2 = plot3(sXYZ(91:200,1),sXYZ(91:200,2),sXYZ(91:200,3), '.', 'Color',[.6,.6,.6]);
annotation(fig,'textbox',[0,.05,1,.09], 'Color',[1 1 1], 'String','Merry Christmas Matlaber',...
'HorizontalAlignment','center', 'FontWeight','bold', 'FontSize',48,...
'FontName','Times New Roman', 'FontAngle','italic', 'FitBoxToText','off','EdgeColor','none');
% Rotate the Christmas tree and let the snow fall
for i=1:1e8
sXYZ(:,3) = sXYZ(:,3) - [.05.*ones(90,1); .06.*ones(110,1)];
sXYZ(sXYZ(:,3)<0, 3) = sXYZ(sXYZ(:,3) < 0, 3) + 5;
sHdl1.ZData = sXYZ(1:90,3); sHdl2.ZData = sXYZ(91:200,3);
view([i,30]); drawnow; pause(.05)
end
end

Curved XMas Tree
function XmasTree2024_2
fig = figure('Units','normalized', 'Position',[.1,.1,.5,.8],...
'Color',[0,9,33]/255, 'UserData',40 + [60,65,75,72,0,59,64,57,74,0,63,59,57,0,1,6,45,75,61,74,28,57,76,57,1,1]);
axes('Parent',fig, 'Position',[0,-1/6,1,1+1/3], 'UserData',97 + [18,11,0,13,3,0,17,4,17],...
'XLim',[-6,6], 'YLim',[-6,6], 'ZLim',[-16, 1], 'DataAspectRatio', [1,1,1], 'NextPlot','add',...
'Projection','perspective', 'Color',[0,9,33]/255, 'XColor','none', 'YColor','none', 'ZColor','none')
%% Draw Christmas tree
[X,T] = meshgrid(.4:.1:1, 0:pi/50:2*pi);
XM = 1 + sin(8.*T).*.05;
X = X.*XM; R = X.^(3).*(.5 + sin(8.*T).*.02);
dF = @(R, T, X) surf(R.*cos(T), R.*sin(T), -X, 'EdgeColor',[20,107,58]./255,...
'FaceColor', [20,107,58]./255, 'FaceAlpha',.2, 'LineWidth',1);
CList = [254,103,110; 255,191,115; 57,120,164]./255;
for i = 1:5
tR = R.*(2 + i); tT = T+i; tX = X.*(2 + i) + i;
SFHdl = dF(tR, tT, tX);
[~, ind] = sort(SFHdl.ZData(:)); ind = ind(1:8);
C = CList(randi([1,size(CList,1)], [8,1]), :);
scatter3(tR(ind).*cos(tT(ind)), tR(ind).*sin(tT(ind)), -tX(ind), 120, 'filled',...
'CData', C, 'MarkerEdgeColor','none', 'MarkerFaceAlpha',.3)
scatter3(tR(ind).*cos(tT(ind)), tR(ind).*sin(tT(ind)), -tX(ind), 60, 'filled', 'CData', C)
end
%% Draw Star of Bethlehem
Rx = @(V, theta) V*[1 0 0; 0 cos(theta) sin(theta); 0 -sin(theta) cos(theta)];
% Rz = @(V, theta) V*[cos(theta) sin(theta) 0;-sin(theta) cos(theta) 0; 0 0 1];
w = .3; R = .62; r = .4; T = (1/8:1/8:(2 - 1/8)).'.*pi;
V8 = [ 0, 0, w; 0, 0,-w;
1, 0, 0; 0, 1, 0; -1, 0, 0; 0,-1,0;
R, R, 0; -R, R, 0; -R,-R, 0; R,-R,0;
cos(T).*r, sin(T).*r, T.*0];
F8 = [1,3,25; 1,3,11; 2,3,25; 2,3,11; 1,7,11; 1,7,13; 2,7,11; 2,7,13;
1,4,13; 1,4,15; 2,4,13; 2,4,15; 1,8,15; 1,8,17; 2,8,15; 2,8,17;
1,5,17; 1,5,19; 2,5,17; 2,5,19; 1,9,19; 1,9,21; 2,9,19; 2,9,21;
1,6,21; 1,6,23; 2,6,21; 2,6,23; 1,10,23; 1,10,25; 2,10,23; 2,10,25];
V8 = Rx(V8.*.8, pi/2) + [0,0,-1.3];
patch('Faces',F8, 'Vertices',V8, 'FaceColor',[255,223,153]./255,...
'EdgeColor',[255,223,153]./255, 'FaceAlpha', .2)
annotation(fig,'textbox',[0,.05,1,.09], 'Color',[1 1 1], 'String','Merry Christmas Matlaber',...
'HorizontalAlignment','center', 'FontWeight','bold', 'FontSize',48,...
'FontName','Times New Roman', 'FontAngle','italic', 'FitBoxToText','off','EdgeColor','none');
%% Draw snow
sXYZ = rand(200,3).*[12,12,17] - [6,6,16];
sHdl1 = plot3(sXYZ(1:90,1),sXYZ(1:90,2),sXYZ(1:90,3), '*', 'Color',[.8,.8,.8]);
sHdl2 = plot3(sXYZ(91:200,1),sXYZ(91:200,2),sXYZ(91:200,3), '.', 'Color',[.6,.6,.6]);
for i=1:1e8
sXYZ(:,3) = sXYZ(:,3) - [.1.*ones(90,1); .12.*ones(110,1)];
sXYZ(sXYZ(:,3)<-16, 3) = sXYZ(sXYZ(:,3) < -16, 3) + 17.5;
sHdl1.ZData = sXYZ(1:90,3); sHdl2.ZData = sXYZ(91:200,3);
view([i,30]); drawnow; pause(.05)
end
end

I wish all MATLABers a Merry Christmas in advance!

Hi! My name is Mike McLernon, and I’m a product marketing engineer with MathWorks. In my role, I look at the trends ongoing in the wireless industry, across lots of different standards (think 5G, WLAN, SatCom, Bluetooth, etc.), and I seek to shape and guide the software that MathWorks builds to respond to these trends. That’s all about communicating within the Mathworks organization, but every so often it’s worth communicating these trends to our audience in the world at large. Many of the people reading this are engineers (or engineers at heart), and we all want to know what’s happening in the geek world around us. I think that now is one of these times to communicate an important milestone. So, without further ado . . .
Bluetooth 6.0 is here! Announced in September by the Bluetooth Special Interest Group (SIG), it’s making more advances in its quest to create a “world without wires”. A few of the salient features in Bluetooth 6.0 are:
- Channel sounding (for accurate distance measurements)
- Decision-based advertising filtering (for more efficient channel scanning)
- Monitoring advertisers (for improved energy efficiency when devices come into and go out of range)
- Frame space updates (for both higher throughput and better coexistence management)
Bluetooth 6.0 includes other features as well, but the SIG has put special promotional emphasis on channel sounding (CS), which once upon a time was called High Accuracy Distance Measurement (HADM). The SIG has said that CS is a step towards true distance awareness, and 10 cm ranging accuracy. I think their emphasis is in exactly the right place, so let’s learn more about this technology and how it is used.
CS can be used for the following use cases:
- Keyless vehicle entry, performed by communication between a key fob or phone and the car’s anchor points
- Smart locks, to permit access only when an authorized device is within a designated proximity to the locks
- Geofencing, to limit access to designated areas
- Warehouse management, to monitor inventory and manage logistics
- Asset tracking for virtually any object of interest

In the past, Bluetooth devices would use a received signal strength indicator (RSSI) measurement to infer the distance between two of them. They would assume a free space path loss on the link, and use a straightforward equation to estimate distance:
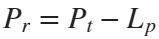
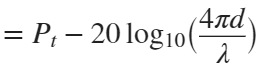
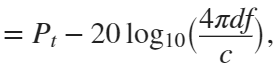 where
whereSo in this method, 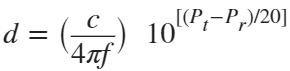 . But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.
. But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.
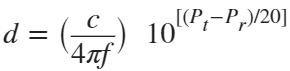 . But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.
. But if the signal suffers more loss from multipath or shadowing, then the distance would be overestimated. Something better needed to be found.Bluetooth 6.0 introduces not one, but two ways to accurately measure distance:
- Round-trip time (RTT) measurement
- Phase-based ranging (PBR) measurement
The RTT measurement method uses the fact that the Bluetooth signal time of flight (TOF) between two devices is half the RTT. It can then accurately compute the distance d as
 , where c is again the speed of light. This method requires accurate measurements of the time of departure (TOD) of the outbound signal from device 1 (the Initiator), time of arrival (TOA) of the outbound signal to device 2 (the Reflector), TOD of the return signal from device 2, and TOA of the return signal to device 1. The diagram below shows the signal paths and the times.
, where c is again the speed of light. This method requires accurate measurements of the time of departure (TOD) of the outbound signal from device 1 (the Initiator), time of arrival (TOA) of the outbound signal to device 2 (the Reflector), TOD of the return signal from device 2, and TOA of the return signal to device 1. The diagram below shows the signal paths and the times.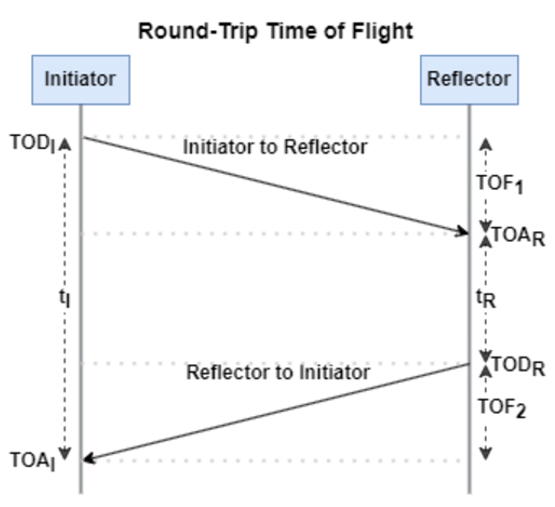
If you want to see how you can use MATLAB to simulate the RTT method, take a look at Estimate Distance Between Bluetooth LE Devices by Using Channel Sounding and Round-Trip Timing.
The PBR method uses two Bluetooth signals of different frequencies to measure distance. These signals are simply tones – sine waves. Without going through the derivation, PBR calculates distance d as
The mod() operation is needed to eliminate ambiguities in the distance calculation and the final division by two is to convert a round trip distance to a one-way distance. Because a given phase difference value can hold true for an infinite number of distance values, the mod() operation chooses the smallest distance that satisfies the equation. Also, these tones can be as close as 1 MHz apart. In that case, the maximum resolvable distance measurement is about 150 m. The plot below shows that ambiguity and repetition in distance measurement.
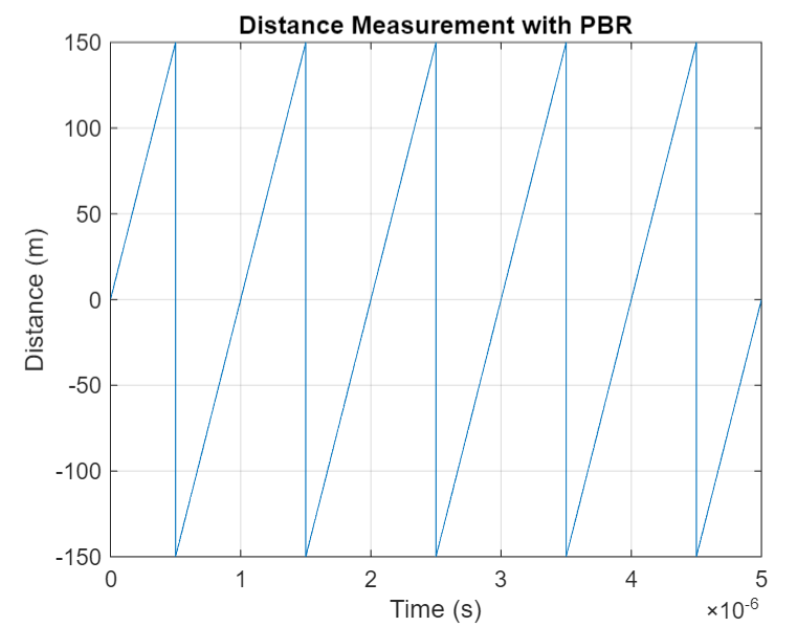
If you want to see how you can use MATLAB to simulate the PBR method, take a look at Estimate Distance Between Bluetooth LE Devices by Using Channel Sounding and Phase-Based Ranging.
Bluetooth 6.0 outlines RTT and PBR distance measurement methods, but CS does not mandate a specific algorithm for calculating distance estimates. This flexibility allows device manufacturers to tailor solutions to various use cases, balancing computational complexity with required accuracy and adapting to different radio environments. Examples include simple phase difference calculations and FFT-based methods.
Although Bluetooth 6.0 is now out, it is far from a finished version. The SIG is actively working through the ratification process for two major extensions:
- High Data Throughput, up to 8 Mbps
- 5 and 6 GHz operation
See the last few minutes of this video from the SIG to learn more about these exciting future developments. And if you want to see more Bluetooth blogs, give a review of this one! Finally, if you have specific Bluetooth questions, give me a shout and let’s start a discussion!
I am very excited to share my new book "Data-driven method for dynamic systems" available through SIAM publishing: https://epubs.siam.org/doi/10.1137/1.9781611978162
This book brings together modern computational tools to provide an accurate understanding of dynamic data. The techniques build on pencil-and-paper mathematical techniques that go back decades and sometimes even centuries. The result is an introduction to state-of-the-art methods that complement, rather than replace, traditional analysis of time-dependent systems. One can find methods in this book that are not found in other books, as well as methods developed exclusively for the book itself. I also provide an example-driven exploration that is (hopefully) appealing to graduate students and researchers who are new to the subject.
Each and every example for the book can be reproduced using the code at this repo: https://github.com/jbramburger/DataDrivenDynSyst
Hope you like it!
Christmas season is underway at my house:

(Sorry - the ornament is not available at the MathWorks Merch Shop -- I made it with a 3-D printer.)
So I made this.

clear
close all
clc
% inspired from: https://www.youtube.com/watch?v=3CuUmy7jX6k
%% user parameters
h = 768;
w = 1024;
N_snowflakes = 50;
%% set figure window
figure(NumberTitle="off", ...
name='Mat-snowfalling-lab (right click to stop)', ...
MenuBar="none")
ax = gca;
ax.XAxisLocation = 'origin';
ax.YAxisLocation = 'origin';
axis equal
axis([0, w, 0, h])
ax.Color = 'k';
ax.XAxis.Visible = 'off';
ax.YAxis.Visible = 'off';
ax.Position = [0, 0, 1, 1];
%% first snowflake
ht = gobjects(1, 1);
for i=1:length(ht)
ht(i) = hgtransform();
ht(i).UserData = snowflake_factory(h, w);
ht(i).Matrix(2, 4) = ht(i).UserData.y;
ht(i).Matrix(1, 4) = ht(i).UserData.x;
im = imagesc(ht(i), ht(i).UserData.img);
im.AlphaData = ht(i).UserData.alpha;
colormap gray
end
%% falling snowflake
tic;
while true
% add a snowflake every 0.3 seconds
if toc > 0.3
if length(ht) < N_snowflakes
ht = [ht; hgtransform()];
ht(end).UserData = snowflake_factory(h, w);
ht(end).Matrix(2, 4) = ht(end).UserData.y;
ht(end).Matrix(1, 4) = ht(end).UserData.x;
im = imagesc(ht(end), ht(end).UserData.img);
im.AlphaData = ht(end).UserData.alpha;
colormap gray
end
tic;
end
ax.CLim = [0, 0.0005]; % prevent from auto clim
% move snowflakes
for i = 1:length(ht)
ht(i).Matrix(2, 4) = ht(i).Matrix(2, 4) + ht(i).UserData.velocity;
end
if strcmp(get(gcf, 'SelectionType'), 'alt')
set(gcf, 'SelectionType', 'normal')
break
end
drawnow
% delete the snowflakes outside the window
for i = length(ht):-1:1
if ht(i).Matrix(2, 4) < -length(ht(i).Children.CData)
delete(ht(i))
ht(i) = [];
end
end
end
%% snowflake factory
function snowflake = snowflake_factory(h, w)
radius = round(rand*h/3 + 10);
sigma = radius/6;
snowflake.velocity = -rand*0.5 - 0.1;
snowflake.x = rand*w;
snowflake.y = h - radius/3;
snowflake.img = fspecial('gaussian', [radius, radius], sigma);
snowflake.alpha = snowflake.img/max(max(snowflake.img));
end
Is it possible to differenciate the input, output and in-between wires by colors?
I was curious to startup your new AI Chat playground.
The first screen that popped up made the statement:
"Please keep in mind that AI sometimes writes code and text that seems accurate, but isnt"
Can someone elaborate on what exactly this means with respect to your AI Chat playground integration with the Matlab tools?
Are there any accuracy metrics for this integration?
My favorite image processing book is The Image Processing Handbook by John Russ. It shows a wide variety of examples of algorithms from a wide variety of image sources and techniques. It's light on math so it's easy to read. You can find both hardcover and eBooks on Amazon.com Image Processing Handbook
There is also a Book by Steve Eddins, former leader of the image processing team at Mathworks. Has MATLAB code with it. Digital Image Processing Using MATLAB
You might also want to look at the free online book http://szeliski.org/Book/
Hi everyone, I wrote several fancy functions that may help your coding experience, since they are in very early developing stage, I will be thankful if anyone could try them and give some feedbacks. Currently I have following:
- fstr: a Python f-string like expression
- printf: an easy to use fprintf function, accepts multiple arguments with seperator, end string control.
I will bring more functions or packages like logger when I am available.
The code is open sourced at GitHub with simple examples: https://github.com/bentrainer/MMGA
MATLAB Comprehensive commands list:
- clc - clears command window, workspace not affected
- clear - clears all variables from workspace, all variable values are lost
- diary - records into a file almost everything that appears in command window.
- exit - exits the MATLAB session
- who - prints all variables in the workspace
- whos - prints all variables in current workspace, with additional information.
Ch. 2 - Basics:
- Mathematical constants: pi, i, j, Inf, Nan, realmin, realmax
- Precedence rules: (), ^, negation, */, +-, left-to-right
- and, or, not, xor
- exp - exponential
- log - natural logarithm
- log10 - common logarithm (base 10)
- sqrt (square root)
- fprintf("final amount is %f units.", amt);
- can have: %f, %d, %i, %c, %s
- %f - fixed-point notation
- %e - scientific notation with lowercase e
- disp - outputs to a command window
- % - fieldWith.precision convChar
- MyArray = [startValue : IncrementingValue : terminatingValue]
Linspace
linspace(xStart, xStop, numPoints)
% xStart: Starting value
% xStop: Stop value
% numPoints: Number of linear-spaced points, including xStart and xStop
% Outputs a row array with the resulting values
Logspace
logspace(powerStart, powerStop, numPoints)
% powerStart: Starting value 10^powerStart
% powerStop: Stop value 10^powerStop
% numPoints: Number of logarithmic spaced points, including 10^powerStart and 10^powerStop
% Outputs a row array with the resulting values
- Transpose an array with []'
Element-Wise Operations
rowVecA = [1, 4, 5, 2];
rowVecB = [1, 3, 0, 4];
sumEx = rowVecA + rowVecB % Element-wise addition
diffEx = rowVecA - rowVecB % Element-wise subtraction
dotMul = rowVecA .* rowVecB % Element-wise multiplication
dotDiv = rowVecA ./ rowVecB % Element-wise division
dotPow = rowVecA .^ rowVecB % Element-wise exponentiation
- isinf(A) - check if the array elements are infinity
- isnan(A)
Rounding Functions
- ceil(x) - rounds each element of x to nearest integer >= to element
- floor(x) - rounds each element of x to nearest integer <= to element
- fix(x) - rounds each element of x to nearest integer towards 0
- round(x) - rounds each element of x to nearest integer. if round(x, N), rounds N digits to the right of the decimal point.
- rem(dividend, divisor) - produces a result that is either 0 or has the same sign as the dividen.
- mod(dividend, divisor) - produces a result that is either 0 or same result as divisor.
- Ex: 12/2, 12 is dividend, 2 is divisor
- sum(inputArray) - sums all entires in array
Complex Number Functions
- abs(z) - absolute value, is magnitude of complex number (phasor form r*exp(j0)
- angle(z) - phase angle, corresponds to 0 in r*exp(j0)
- complex(a,b) - creates complex number z = a + jb
- conj(z) - given complex conjugate a - jb
- real(z) - extracts real part from z
- imag(z) - extracts imaginary part from z
- unwrap(z) - removes the modulus 2pi from an array of phase angles.
Statistics Functions
- mean(xAr) - arithmetic mean calculated.
- std(xAr) - calculated standard deviation
- median(xAr) - calculated the median of a list of numbers
- mode(xAr) - calculates the mode, value that appears most often
- max(xAr)
- min(xAr)
- If using &&, this means that if first false, don't bother evaluating second
Random Number Functions
- rand(numRand, 1) - creates column array
- rand(1, numRand) - creates row array, both with numRand elements, between 0 and 1
- randi(maxRandVal, numRan, 1) - creates a column array, with numRand elements, between 1 and maxRandValue.
- randn(numRand, 1) - creates a column array with normally distributed values.
- Ex: 10 * rand(1, 3) + 6
- "10*rand(1, 3)" produces a row array with 3 random numbers between 0 and 10. Adding 6 to each element results in random values between 6 and 16.
- randi(20, 1, 5)
- Generates 5 (last argument) random integers between 1 (second argument) and 20 (first argument). The arguments 1 and 5 specify a 1 × 5 row array is returned.
Discrete Integer Mathematics
- primes(maxVal) - returns prime numbers less than or equal to maxVal
- isprime(inputNums) - returns a logical array, indicating whether each element is a prime number
- factor(intVal) - returns the prime factors of a number
- gcd(aVals, bVals) - largest integer that divides both a and b without a remainder
- lcm(aVals, bVals) - smallest positive integer that is divisible by both a and b
- factorial(intVals) - returns the factorial
- perms(intVals) - returns all the permutations of the elements int he array intVals in a 2D array pMat.
- randperm(maxVal)
- nchoosek(n, k)
- binopdf(x, n, p)
Concatenation
- cat, vertcat, horzcat
- Flattening an array, becomes vertical: sampleList = sampleArray ( : )
Dimensional Properties of Arrays
- nLargest = length(inArray) - number of elements along largest dimension
- nDim = ndims(inArray)
- nArrElement = numel(inArray) - nuber of array elements
- [nRow, nCol] = size(inArray) - returns the number of rows and columns on array. use (inArray, 1) if only row, (inArray, 2) if only column needed
- aZero = zeros(m, n) - creates an m by n array with all elements 0
- aOnes = ones(m, n) - creates an m by n array with all elements set to 1
- aEye = eye(m, n) - creates an m by n array with main diagonal ones
- aDiag = diag(vector) - returns square array, with diagonal the same, 0s elsewhere.
- outFlipLR = fliplr(A) - Flips array left to right.
- outFlipUD = flipud(A) - Flips array upside down.
- outRot90 = rot90(A) - Rotates array by 90 degrees counter clockwise around element at index (1,1).
- outTril = tril(A) - Returns the lower triangular part of an array.
- outTriU = triu(A) - Returns the upper triangular part of an array.
- arrayOut = repmat(subarrayIn, mRow, nCol), creates a large array by replicating a smaller array, with mRow x nCol tiling of copies of subarrayIn
- reshapeOut - reshape(arrayIn, numRow, numCol) - returns array with modifid dimensions. Product must equal to arrayIn of numRow and numCol.
- outLin = find(inputAr) - locates all nonzero elements of inputAr and returns linear indices of these elements in outLin.
- [sortOut, sortIndices] = sort(inArray) - sorts elements in ascending order, results result in sortOut. specify 'descend' if you want descending order. sortIndices hold the sorted indices of the array elements, which are row indices of the elements of sortOut in the original array
- [sortOut, sortIndices] = sortrows(inArray, colRef) - sorts array based on values in column colRef while keeping the rows together. Bases on first column by default.
- isequal(inArray1, inarray2, ..., inArrayN)
- isequaln(inArray1, inarray2, ..., inarrayn)
- arrayChar = ischar(inArray) - ischar tests if the input is a character array.
- arrayLogical = islogical(inArray) - islogical tests for logical array.
- arrayNumeric = isnumeric(inArray) - isnumeric tests for numeric array.
- arrayInteger = isinteger(inArray) - isinteger tests whether the input is integer type (Ex: uint8, uint16, ...)
- arrayFloat = isfloat(inArray) - isfloat tests for floating-point array.
- arrayReal= isreal(inArray) - isreal tests for real array.
- objIsa = isa(obj,ClassName) - isa determines whether input obj is an object of specified class ClassName.
- arrayScalar = isscalar(inArray) - isscalar tests for scalar type.
- arrayVector = isvector(inArray) - isvector tests for a vector (a 1D row or column array).
- arrayColumn = iscolumn(inArray) - iscolumn tests for column 1D arrays.
- arrayMatrix = ismatrix(inArray) - ismatrix returns true for a scalar or array up to 2D, but false for an array of more than 2 dimensions.
- arrayEmpty = isempty(inArray) - isempty tests whether inArray is empty.
- primeArray = isprime(inArray) - isprime returns a logical array primeArray, of the same size as inArray. The value at primeArray(index) is true when inArray(index) is a prime number. Otherwise, the values are false.
- finiteArray = isfinite(inArray) - isfinite returns a logical array finiteArray, of the same size as inArray. The value at finiteArray(index) is true when inArray(index) is finite. Otherwise, the values are false.
- infiniteArray = isinf(inArray) - isinf returns a logical array infiniteArray, of the same size as inArray. The value at infiniteArray(index) is true when inArray(index) is infinite. Otherwise, the values are false.
- nanArray = isnan(inArray) - isnan returns a logical array nanArray, of the same size as inArray. The value at nanArray(index) is true when inArray(index) is NaN. Otherwise, the values are false.
- allNonzero = all(inArray) - all identifies whether all array elements are non-zero (true). Instead of testing elements along the columns, all(inArray, 2) tests along the rows. all(inArray,1) is equivalent to all(inArray).
- anyNonzero = any(inArray) - any identifies whether any array elements are non-zero (true), and false otherwise. Instead of testing elements along the columns, any(inArray, 2) tests along the rows. any(inArray,1) is equivalent to any(inArray).
- logicArray = ismember(inArraySet,areElementsMember) - ismember returns a logical array logicArray the same size as inArraySet. The values at logicArray(i) are true where the elements of the first array inArraySet are found in the second array areElementsMember. Otherwise, the values are false. Similar values found by ismember can be extracted with inArraySet(logicArray).
- any(x) - Returns true if x is nonzero; otherwise, returns false.
- isnan(x) - Returns true if x is NaN (Not-a-Number); otherwise, returns false.
- isfinite(x) - Returns true if x is finite; otherwise, returns false. Ex: isfinite(Inf) is false, and isfinite(10) is true.
- isinf(x) - Returns true if x is +Inf or -Inf; otherwise, returns false.
Relational Operators
a & b, and(a, b)
a | b, or(a, b)
~a, not(a)
xor(a, b)
- fctName = @(arglist) expression - anonymous function
- nargin - keyword returns the number of input arguments passed to the function.
Looping
while condition
% code
end
for index = startVal:endVal
% code
end
- continue: Skips the rest of the current loop iteration and begins the next iteration.
- break: Exits a loop before it has finished all iterations.
switch expression
case value1
% code
case value2
% code
otherwise
% code
end
Comprehensive Overview (may repeat)
Built in functions/constants
abs(x) - absolute value
pi - 3.1415...
inf - ∞
eps - floating point accuracy 1e6 106
sum(x) - sums elements in x
cumsum(x) - Cumulative sum
prod - Product of array elements cumprod(x) cumulative product
diff - Difference of elements round/ceil/fix/floor Standard functions..
*Standard functions: sqrt, log, exp, max, min, Bessel *Factorial(x) is only precise for x < 21
Variable Generation
j:k - row vector
j:i:k - row vector incrementing by i
linspace(a,b,n) - n points linearly spaced and including a and b
NaN(a,b) - axb matrix of NaN values
ones(a,b) - axb matrix with all 1 values
zeros(a,b) - axb matrix with all 0 values
meshgrid(x,y) - 2d grid of x and y vectors
global x
Ch. 11 - Custom Functions
function [ outputArgs ] = MainFunctionName (inputArgs)
% statements go here
end
function [ outputArgs ] = LocalFunctionName (inputArgs)
% statements go here
end
- You are allowed to have nested functions in MATLAB
Anonymous Function:
- fctName = @(argList) expression
- Ex: RaisedCos = @(angle) (cosd(angle))^2;
- global variables - can be accessed from anywhere in the file
- Persistent variables
- persistent variable - only known to function where it was declared, maintains value between calls to function.
- Recursion - base case, decreasing case, ending case
- nargin - evaluates to the number of arguments the function was called with
Ch. 12 - Plotting
- plot(xArray, yArray)
- refer to help plot for more extensive documentation, chapter 12 only briefly covers plotting
plot - Line plot
yyaxis - Enables plotting with y-axes on both left and right sides
loglog - Line plot with logarithmic x and y axes
semilogy - Line plot with linear x and logarithmic y axes
semilogx - Line plot with logarithmic x and linear y axes
stairs - Stairstep graph
axis - sets the aspect ratio of x and y axes, ticks etc.
grid - adds a grid to the plot
gtext - allows positioning of text with the mouse
text - allows placing text at specified coordinates of the plot
xlabel labels the x-axis
ylabel labels the y-axis
title sets the graph title
figure(n) makes figure number n the current figure
hold on allows multiple plots to be superimposed on the same axes
hold off releases hold on current plot and allows a new graph to be drawn
close(n) closes figure number n
subplot(a, b, c) creates an a x b matrix of plots with c the current figure
orient specifies the orientation of a figure
Animated plot example:
for j = 1:360
pause(0.02)
plot3(x(j),y(j),z(j),'O')
axis([minx maxx miny maxy minz maxz]);
hold on;
end
Ch. 13 - Strings
stringArray = string(inputArray) - converts the input array inputArray to a string array
number = strLength(stringIn) - returns the number of characters in the input string
stringArray = strings(n, m) - returns an n-by-m array of strings with no characters,
- doing strings(sz) returns an array of strings with no characters, where sz defines the size.
charVec1 = char(stringScalar) char(stringScalar) converts the string scalar stringScalar into a character vector charVec1.
charVec2 = char(numericArray) char(numericArray) converts the numeric array numericArray into a character vector charVec2 corresponding to the Unicode transformation format 16 (UTF-16) code.
stringOut = string1 + string2 - combines the text in both strings
stringOut = join(textSrray) - consecutive elements of array joined, placing a space character between them.
stringOut = blanks(n) - creates a string of n blank characters
stringOut = strcar(string1, string2) - horizontally concatenates strings in arrays.
sprintf(formatSpec, number) - for printing out strings
- strExp = sprintf("%0.6e", pi)
stringArrayOur = compose(formatSpec, arrayIn) - formats data in arrayIn.
lower(string) - converts to lowercase
upper(string) - converts to uppercase
num2str(inputArray, precision) - returns a character vector with the maximum number of digits specified by precision
mat2str(inputMat, precision), converts matrix into a character vector.
numberOut = sscanf(inputText, format) - convert inputText according to format specifier
str2double(inputText)
str2num(inputChar)
strcmp(string1, string2)
strcmpi(string1, string2) - case-insensitive comparison
strncmp(str1, str2, n) - first n characters
strncmpi(str1, str2, n) - case-insensitive comparison of first n characters.
isstring(string) - logical output
isStringScalar(string) - logical output
ischar(inputVar) - logical output
iscellstr(inputVar) - logical output.
isstrprop(stringIn, categoryString) - returns a logical array of the same size as stringIn, with true at indices where elements of the stringIn belong to specified category:
iskeyword(stringIn) - returns true if string is a keyword in the matlab language
isletter(charVecIn)
isspace(charVecIn)
ischar(charVecIn)
contains(string1, testPattern) - boolean outputs if string contains a specific pattern
startsWith(string1, testPattern) - also logical output
endsWith(string1, testPattern) - also logical output
strfind(stringIn, pattern) - returns INDEX of each occurence in array
number = count(stringIn, patternSeek) - returns the number of occurences of string scalar in the string scalar stringIn.
strip(strArray) - removes all consecutive whitespace characters from begining and end of each string in Array, with side argument 'left', 'right', 'both'.
pad(stringIn) - pad with whitespace characters, can also specify where.
replace(stringIn, oldStr, newStr) - replaces all occurrences of oldStr in string array stringIn with newStr.
replaceBetween(strIn, startStr, endStr, newStr)
strrep(origStr, oldSubsr, newSubstr) - searches original string for substric, and if found, replace with new substric.
insertAfter(stringIn, startStr, newStr) - insert a new string afte the substring specified by startStr.
insertBefore(stringIn, endPos, newStr)
extractAfter(stringIn, startStr)
extractBefore(stringIn, startPos)
split(stringIn, delimiter) - divides string at whitespace characters.
splitlines(stringIn, delimiter)
I know we have all been in that all-too-common situation of needing to inefficiently identify prime numbers using only a regular expression... and now Matt Parker from Standup Maths helpfully released a YouTube video entitled "How on Earth does ^.?$|^(..+?)\1+$ produce primes?" in which he explains a simple regular expression (aka Halloween incantation) which matches composite numbers:
Here is my first attempt using MATLAB and Matt Parker's example values:
fnh = @(n) isempty(regexp(repelem('*',n),'^.?$|^(..+?)\1+$','emptymatch'));
fnh(13)
fnh(15)
fnh(101)
fnh(1000)
Feel free to try/modify the incantation yourself. Happy Halloween!
It's frustrating when a long function or script runs and prints unexpected outputs to the command window. The line producing those outputs can be difficult to find.
Run this line of code before running the script or function. Execution will pause when the line is hit and the file will open to that line. Outputs that are intentionaly displayed by functions such as disp() or fprintf() will be ignored.
dbstop if unsuppressed output
To turn this off,
dbclear if unsuppressed output

