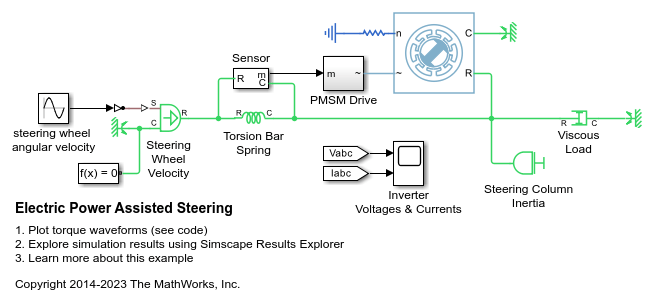
PMSM
Permanent magnet synchronous motor with sinusoidal flux distribution
Libraries:
Simscape /
Electrical /
Electromechanical /
Permanent Magnet
Description
The PMSM block models a permanent magnet synchronous motor with a three-phase wye-wound stator. The figure shows the equivalent electrical circuit for the stator windings.

You can also model the permanent magnet synchronous motor either in a delta-wound or
in an open-end configuration by setting Winding type to
Delta-wound or Open-end,
respectively.
You can choose different built-in parameterizations for this block. For more information, see the Predefined Parameterization section.
Motor Construction
This figure shows the motor construction with a single pole-pair on the rotor.

Permanent magnets generate a rotor magnetic field that creates a sinusoidal rate of change of flux based on the rotor angle.
For the axes convention, when you set the Rotor angle
definition parameter to Angle between the a-phase
magnetic axis and the d-axis, the a-phase and
permanent magnet fluxes align when the rotor mechanical angle,
θr, is zero. When you set the
Rotor angle definition parameter to Angle
between the a-phase magnetic axis and the q-axis, the rotor
mechanical angle is the angle between the a-phase magnetic axis
and the rotor q-axis.
Equations
Voltages across the stator windings are
where:
va, vb, and vc are the individual phase voltages across the stator windings.
Rs is the equivalent resistance of each stator winding.
ia, ib, and ic are the currents flowing in the stator windings.
and are the rates of change for the magnetic flux in each stator winding.
The permanent magnet and the three windings contribute to the total flux linking each winding. The total flux is
where:
ψa, ψb, and ψc are the total fluxes linking each stator winding.
Laa, Lbb, and Lcc are the self-inductances of the stator windings.
Lab, Lac, Lba, and so on, are the mutual inductances of the stator windings.
ψam, ψbm, and ψcm are the permanent magnet fluxes linking the stator windings.
The inductances in the stator windings are functions of the rotor electrical angle and defined by
where:
θr is the rotor mechanical angle.
θe is the rotor electrical angle.
rotor offset is
0if you define the rotor electrical angle with respect to the d-axis, or-pi/2if you define the rotor electrical angle with respect to the q-axis.Ls is the stator self-inductance per phase. This value is the average self-inductance of each of the stator windings.
Lm is the stator inductance fluctuation. This value is the amount the self-inductance and mutual inductance fluctuate with the changing of the rotor angle.
Ms is the stator mutual inductance. This value is the average mutual inductance between the stator windings.
The permanent magnet flux linking winding a is a maximum when θe = 0° and zero when θe = 90°. Therefore, the linked motor flux is defined by:
where ψm is the permanent magnet flux linkage.
Simplified Electrical Equations
Applying Park’s transformation to the block electrical equations produces an expression for torque that is independent of the rotor angle.
Park’s transformation is defined by:
where θe is the electrical angle defined as Nθr. N is the number of pole pairs.
Using Park's transformation on the stator winding voltages and currents transforms them to the dq0 frame, which is independent of the rotor angle:
Applying Park’s transformation to the first two electrical equations produces these equations that define the block behavior:
where:
Ld = Ls + Ms + 3/2 Lm. Ld is the stator d-axis inductance.
Lq = Ls + Ms − 3/2 Lm. Lq is the stator q-axis inductance.
L0 = Ls – 2Ms. L0 is the stator zero-sequence inductance.
ω is the rotor mechanical rotational speed.
N is the number of rotor permanent magnet pole pairs.
T is the rotor torque. Torque flows from the motor case (block physical port C) to the motor rotor (block physical port R).
The PMSM block uses the original, non-orthogonal implementation of the Park transform. If you try to apply the alternative implementation, you get different results for the dq0 voltage and currents.
Alternative Flux Linkage Parameterization
You can parameterize the motor using the back EMF or torque constants which are more commonly given on motor datasheets by using the Permanent magnet flux linkage parameter.
The back EMF constant is the peak voltage induced by the permanent magnet in the per-unit rotational speed of each of the phases. The relationship between the peak permanent magnet flux linkage and the back EMF is:
The back EMF, eph, for one phase is:
The torque constant is the peak torque induced by the per-unit current of each of the phases. It is numerically identical in value to the back EMF constant when both are expressed in SI units:
When Ld=Lq and the currents in all three phases are balanced, the combined torque T is:
where Ipk is the peak current in any of the three windings.
The factor 3/2 follows from this being the steady-state sum of the torques from all phases. Therefore, the torque constant kt can also be:
where T is the measured total torque when testing with a balanced three-phase current with peak line voltage Ipk. The RMS line current is:
Calculating Iron Losses
Iron losses are divided into two terms, one representing the main magnetizing path, and the other representing the cross-tooth tip path that becomes active during field weakened operation. The iron losses model, which is based on the work of Mellor [3].
The term representing the main magnetizing path depends on the induced RMS line-to-neutral stator voltage, :
This is the dominant term during no-load operation. k is the back emf constant relating RMS volts per Hz. It is defined as , where f is the electrical frequency. The first term on the right-hand side is the magnetic hysteresis loss, the second is the eddy current loss and the third is the excess loss. The three coefficients appearing on the numerators are derived from the values that you provide for the open-circuit hysteresis, eddy, and excess losses.
The term representing the cross-tooth tip path becomes important when a demagnetizing field is set up and can be determined from a finite element analysis short-circuit test. It depends on the RMS emf associated with the cross-tooth tip flux, :
The three numerator terms are derived from the values you provide for the short-circuit hysteresis, eddy, and excess losses.
Predefined Parameterization
There are multiple available built-in parameterizations for the PMSM block.
This pre-parameterization data allows you to set up the block to represent components by specific suppliers. The parameterizations of these permanent magnet synchronous motors match the manufacturer data sheets. To load a predefined parameterization, double-click the PMSM block, click the <click to select> hyperlink of the Selected part parameter and, in the Block Parameterization Manager window, select the part you want to use from the list of available components.
Note
The predefined parameterizations of Simscape™ components use available data sources for the parameter values. Engineering judgement and simplifying assumptions are used to fill in for missing data. As a result, expect deviations between simulated and actual physical behavior. To ensure accuracy, validate the simulated behavior against experimental data and refine component models as necessary.
For more information about pre-parameterization and for a list of the available components, see List of Pre-Parameterized Components.
Model Thermal Effects
You can expose thermal ports to model the effects of losses that convert power to heat. To expose the thermal ports, set the Modeling option parameter to either:
No thermal port— The block contains expanded electrical conserving ports associated with the stator windings, but does not contain thermal ports.Show thermal port— The block contains expanded electrical conserving ports associated with the stator windings and thermal conserving ports for each of the windings and for the rotor.
For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. You can specify nominal values using different sources, including the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
Examples
Ports
Conserving
Parameters
References
[1] Kundur, P. Power System Stability and Control. New York, NY: McGraw Hill, 1993.
[2] Anderson, P. M. Analysis of Faulted Power Systems. Hoboken, NJ: Wiley-IEEE Press, 1995.
[3] Mellor, P.H., R. Wrobel, and D. Holliday. “A computationally efficient iron loss model for brushless AC machines that caters for rated flux and field weakened operation.” IEEE Electric Machines and Drives Conference. May 2009.