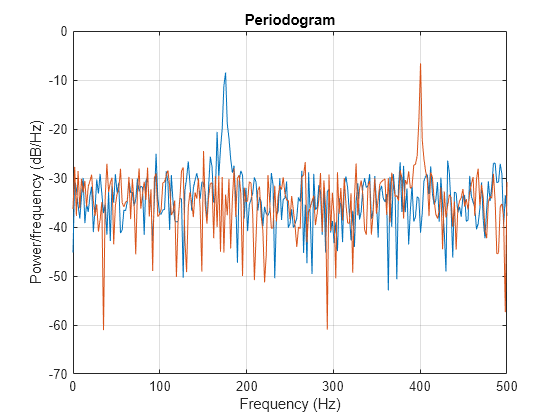
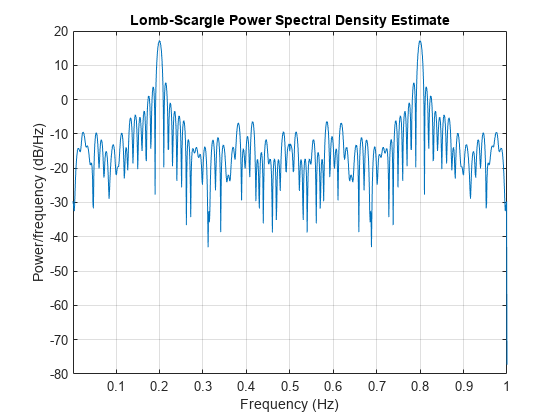
plomb
Lomb-Scargle periodogram
Syntax
Description
[
returns the Lomb-Scargle power spectral density (PSD) estimate,
pxx,f]
= plomb(x,t)pxx, of a signal, x, that is
sampled at the instants specified in t.
t must increase monotonically but need not be uniformly
spaced. All elements of t must be nonnegative.
pxx is evaluated at the frequencies returned in
f.
If
xis a vector, it is treated as a single channel.If
xis a matrix, thenplombcomputes the PSD independently for each column and returns it in the corresponding column ofpxx.
x or t can contain
NaNs or NaTs. These values are treated
as missing data and excluded from the spectrum computation.
[
estimates the PSD up to a maximum frequency, pxx,f]
= plomb(___,fmax)fmax, using
any of the input arguments from previous syntaxes. If the signal is sampled at
N non-NaN instants, and Δt is the time difference between the first and the last of them,
then pxx is returned at
round(fmax / fmin)
points, where fmin = 1/(4 × N × ts) is the smallest frequency at which pxx is
computed and the average sample time is ts = Δt/(N – 1). fmax defaults to 1/(2 × ts), which for uniformly sampled signals corresponds to the
Nyquist frequency.
[
specifies an integer oversampling factor, pxx,f]
= plomb(___,fmax,ofac)ofac. The use of
ofac to interpolate or smooth a spectrum resembles the
zero-padding technique for FFT-based methods. pxx is again
returned at
round(fmax/fmin)
frequency points, but the minimum frequency considered in this case is
1/(ofac × N × ts).
ofac defaults to 4.
[___,
returns the power-level threshold, pth] = plomb(___,'Pd',pdvec)pth, such that a peak
with a value larger than pth has a probability
pdvec of being a true signal peak and not the result of
random fluctuations. pdvec can be a vector. Every element
of pdvec must be greater than 0 and smaller than 1. Each
row of pth corresponds to an element of
pdvec. pth has the same number of
channels as x. This option is not available if you specify
the output frequencies in fvec.
[
returns the PSD estimate of pxx,w]
= plomb(x)x evaluated at a set of evenly
spaced normalized frequencies, w, spanning the Nyquist
interval. Use NaNs to specify missing samples. All of the
above options are available for normalized frequencies. To access them, specify
an empty array as the second input.
plomb(___) with no output arguments plots the
Lomb-Scargle periodogram PSD estimate in the current figure window.
Examples
Input Arguments
Output Arguments
More About
References
[1] Horne, James H., and Sallie L. Baliunas. "A Prescription for Period Analysis of Unevenly Sampled Time Series." Astrophysical Journal. Vol. 302, 1986, pp. 757–763.
[2] Lomb, Nicholas R. "Least-Squares Frequency Analysis of Unequally Spaced Data." Astrophysics and Space Science. Vol. 39, 1976, pp. 447–462.
[3] Press, William H., and George B. Rybicki. "Fast Algorithm for Spectral Analysis of Unevenly Sampled Data." Astrophysical Journal. Vol. 338, 1989, pp. 277–280.
[4] Scargle, Jeffrey D. "Studies in Astronomical Time Series Analysis. II. Statistical Aspects of Spectral Analysis of Unevenly Spaced Data." Astrophysical Journal. Vol. 263, 1982, pp. 835–853.
Extended Capabilities
Version History
Introduced in R2014b