periodogram
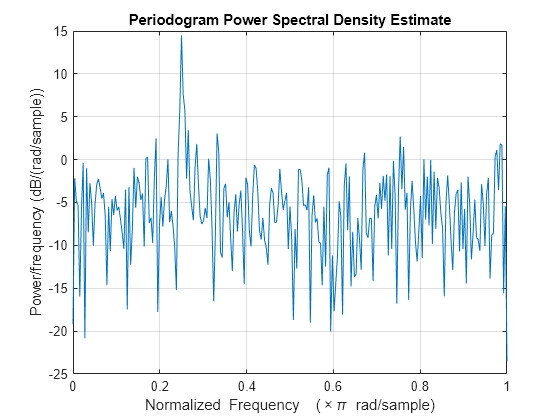
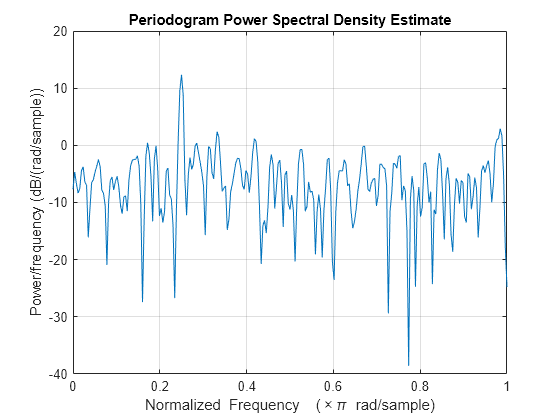
Periodogram power spectral density estimate
Syntax
Description
pxx = periodogram(x)pxx, of the input signal, x, found
using a rectangular window. When x is a vector, it is
treated as a single channel. When x is a matrix, the PSD is
computed independently for each column and stored in the corresponding column of
pxx. If x is real-valued,
pxx is a one-sided PSD estimate. If
x is complex-valued, pxx is a
two-sided PSD estimate. The number of points, nfft, in the
discrete Fourier transform (DFT) is the maximum of 256 or the next power of two
greater than the signal length.
pxx = periodogram(x,window,nfft)nfft points in the discrete Fourier transform (DFT).
If nfft is greater than the signal length,
x is zero-padded to length nfft.
If nfft is less than the signal length, the signal is
wrapped modulo nfft and summed using
datawrap. For example, the input signal [1 2 3
4 5 6 7 8] with nfft equal to 4 results in
the periodogram of sum([1 5; 2 6; 3 7; 4 8],2).
[
returns a frequency vector, pxx,f] = periodogram(___,fs)f, in cycles per unit time. The
sample rate, fs, is the number of samples per unit time. If
the unit of time is seconds, then f is in cycles/second
(Hz). For real-valued signals, f spans the interval
[0,fs/2] when nfft is even and
[0,fs/2) when nfft is odd. For
complex-valued signals, f spans the interval
[0,fs). fs must be the fourth
input to periodogram. To input a sample rate and still use
the default values of the preceding optional arguments, specify these arguments
as empty, [].
[
returns the two-sided periodogram estimates at the frequencies specified in the
vector. The vector pxx,f] = periodogram(x,window,f,fs)f must contain at least two elements,
because otherwise the function interprets it as nfft. The
frequencies in f are in cycles per unit time. The sample
rate, fs, is the number of samples per unit time. If the
unit of time is seconds, then f is in cycles/second
(Hz).
[___,
returns the pxxc] = periodogram(___,'ConfidenceLevel',probability)probability × 100% confidence
intervals for the PSD estimate in pxxc.
[___] = periodogram(___,
returns the PSD estimate if spectrumtype)spectrumtype is specified as
'psd' and returns the power spectrum if
spectrumtype is specified as
'power'.
periodogram(___) with no output arguments
plots the periodogram PSD estimate or power spectrum in the current figure
window.
Examples
Input Arguments
Output Arguments
More About
References
[1] Auger, François, and Patrick Flandrin. "Improving the Readability of Time-Frequency and Time-Scale Representations by the Reassignment Method." IEEE® Transactions on Signal Processing. Vol. 43, May 1995, pp. 1068–1089.
[2] Fulop, Sean A., and Kelly Fitz. "Algorithms for computing the time-corrected instantaneous frequency (reassigned) spectrogram, with applications." Journal of the Acoustical Society of America. Vol. 119, January 2006, pp. 360–371.