Reconstruct Phase Space
Reconstruct phase space of a uniformly sampled signal in the Live Editor
Description
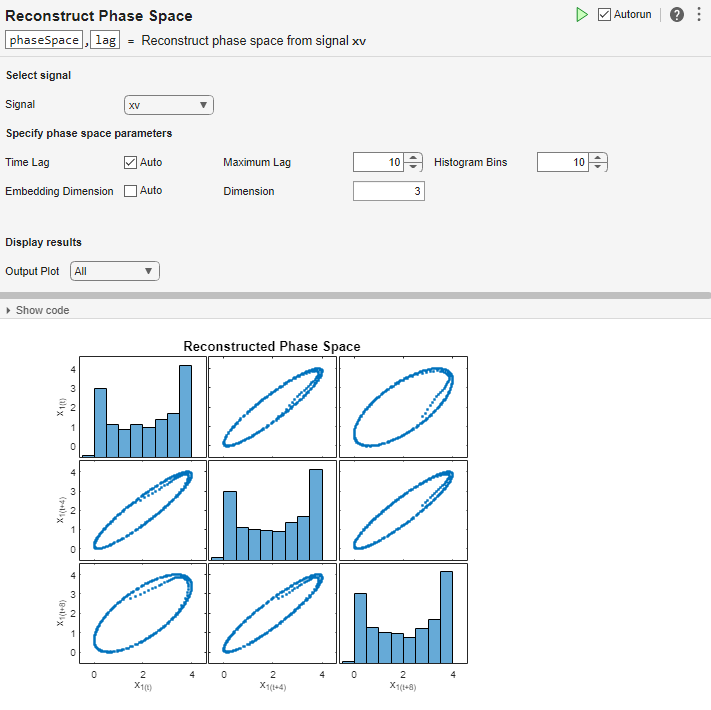
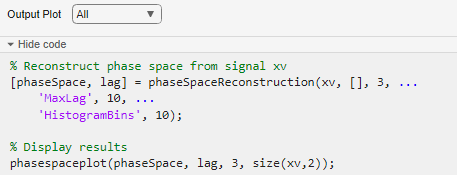
The Reconstruct Phase Space task lets you interactively reconstruct phase space of a uniformly sampled signal. The task automatically generates MATLAB® code for your live script. For more information about Live Editor tasks generally, see Add Interactive Tasks to a Live Script.
Phase space reconstruction is useful to verify the system order and reconstruct all
dynamic system variables, while preserving system properties. Reconstructing the phase space
is performed when limited data is available, or when the phase space dimension and lag values
are unknown. Also, the nonlinear features approximateEntropy, correlationDimension, and lyapunovExponent use phase space reconstruction as the first step of the
computation. For more information about phase space reconstruction, see phaseSpaceReconstruction.
Open the Task
To add the Reconstruct Phase Space task to a live script in the MATLAB Editor:
On the Live Editor tab, select Task > Reconstruct Phase Space.
In a code block in your script, type a relevant keyword, such as
phaseorphase space. SelectReconstruct Phase Spacefrom the suggested command completions.
Examples
Related Examples
Parameters
Version History
Introduced in R2019b