correlationDimension
Measure of chaotic signal complexity
Syntax
Description
corDim = correlationDimension(X)X. Correlation dimension is the measure of
dimensionality of the space occupied by a set of random points.
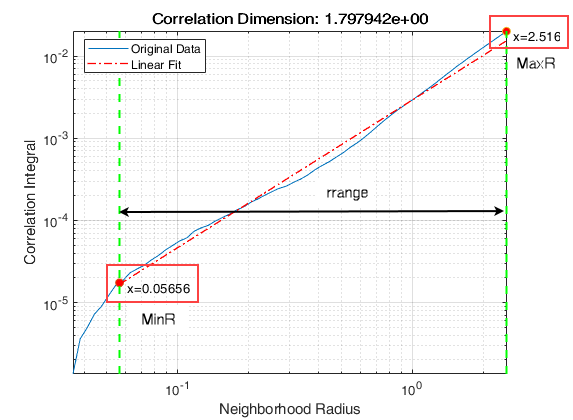
corDim is estimated as the slope of the correlation
integral versus the range of radius of similarity. Use
correlationDimension as a characteristic measure to
distinguish between deterministic chaos and random noise, to detect potential
faults.[1]
[
additionally estimates the range of radius of similarity and correlation
integral of the uniformly sampled time-domain signal corDim,rRange,corInt] = correlationDimension(___)X.
Correlation integral is the mean probability that the states of a system are
close at two different time intervals, which reflects self-similarity.
___ = correlationDimension(___,
estimates the correlation dimension with additional options specified by one or
more Name,Value)Name,Value pair arguments.
correlationDimension(___) with no output
arguments creates a correlation integral versus neighborhood radius plot.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
Correlation dimension is computed in the following way,
The
correlationDimensionfunction first generates a delayed reconstruction Y1:N with embedding dimension m, and lag τ.The software then calculates the number of with-in range points, at point i, given by,
where 1 is the indicator function, and R is the radius of similarity, given by, R = exp(linspace(log(rmin), log(rmax), N)). Here, rmin is
MinRadius, rmax isMaxRadius, and N isNumPoints.The correlation dimension
corDimis the slope of C(R) vs. R where, the correlation integral C(R) is defined as,
References
[1] Caesarendra, Wahyu & Kosasih, P & Tieu, Kiet & Moodie, Craig. "An application of nonlinear feature extraction-A case study for low speed slewing bearing condition monitoring and prognosis." IEEE/ASME International Conference on Advanced Intelligent Mechatronics: Mechatronics for Human Wellbeing, AIM 2013.1713-1718. 10.1109/AIM.2013.6584344.
[2] Theiler, James. "Efficient algorithm for estimating the correlation dimension from a set of discrete points". American Physical Society. Physical Review A 1987/11/1. Volume 36. Issue 9. Pages 44-56.
Extended Capabilities
Version History
Introduced in R2018a