tetramesh
Tetrahedron mesh plot
Description
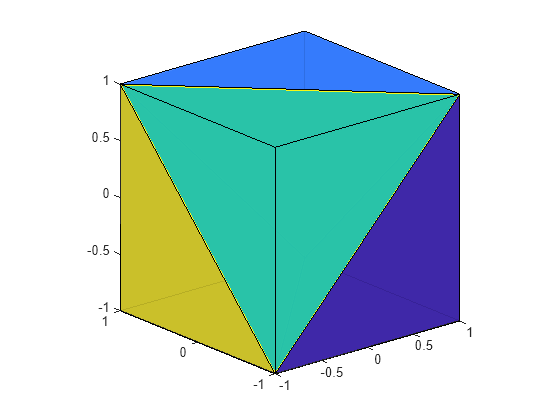
tetramesh( plots the
3-D tetrahedron mesh defined by the tetrahedron connectivity matrix T,X)T and
the points X.
T is an m-by-4 matrix that
specifies the vertices of m tetrahedra. X is an
n-by-3 matrix that specifies the Cartesian
coordinates of n points. Each row of T contains
indices into X that specify the 4 vertices of a tetrahedron.
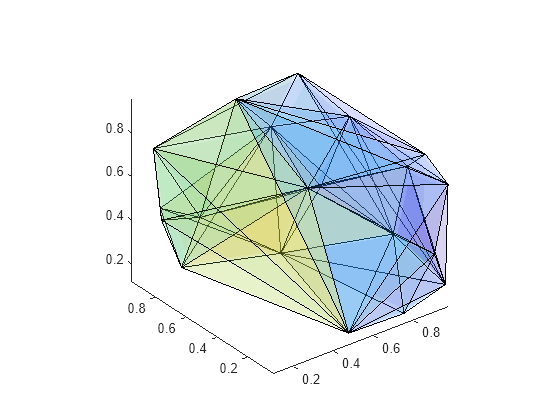
tetramesh( plots the tetrahedron mesh
defined by a 3-D TR)triangulation or
delaunayTriangulation object.
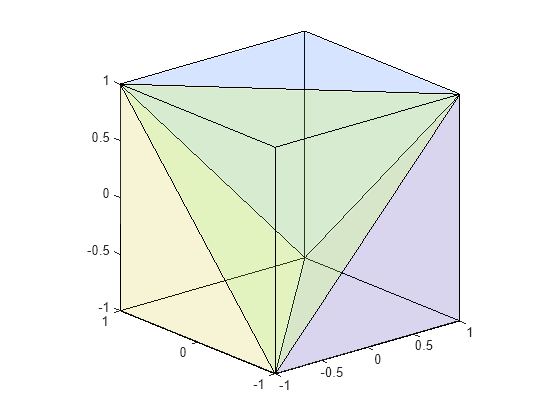
tetramesh(___, also specifies
the face color of each tetrahedron using a vector of colormap indices.c)
tetramesh(___,
specifies one or more properties of the mesh plot using name-value arguments. For example,
Name,Value)'LineWidth',2 sets the edge width to 2
points.
h = tetramesh(___) returns a vector of tetrahedron
handles. Each handle of h is a patch object used to create the mesh plot of each tetrahedron. Use
h(i) to query and modify properties of the plot of each tetrahedron.
For more information, see Patch Properties.
Examples
Input Arguments
Name-Value Arguments
Version History
Introduced before R2006a
See Also
trimesh | trisurf | patch | delaunayn | triangulation | delaunayTriangulation | freeBoundary