Matrix Representation of Geometric Transformations
You can represent a linear geometric transformation as a numeric matrix. Each type of transformation, such as translation, scaling, rotation, and reflection, is defined using a matrix whose elements follow a specific pattern. You can combine multiple transformations by taking a composite of the matrices representing the transformations. For more information, see Create Composite 2-D Affine Transformations.
2-D Affine Transformations
The table lists 2-D affine transformations with the transformation matrix used to define
them. For 2-D affine transformations, the last row must be [0 0
1].
Use combinations of 2-D translation matrices to create a
transltform2dobject representing a translation transformation.Use combinations of 2-D translation and rotation matrices to create a
rigidtform2dobject representing a nonreflective rigid transformation.Use combinations of 2-D translation, rotation, and scaling matrices to create a
simtform2dobject representing a nonreflective similarity transformation.Use any combination of 2-D transformation matrices to create an
affinetform2dobject representing a general affine transformation.
| 2-D Affine Transformation | Example (Original and Transformed Image) | Transformation Matrix | |
|---|---|---|---|
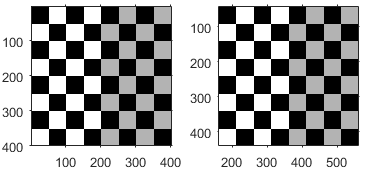
| Translation |
| tx specifies the displacement along the x axis ty specifies the displacement along the y axis. For more information about pixel coordinates, see Image Coordinate Systems. | |
| Scale |
| sx specifies the scale factor along the x axis sy specifies the scale factor along the y axis. | |
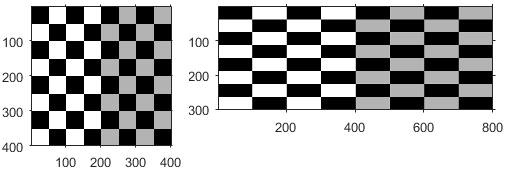
| Shear |
| shx specifies the shear factor along the x axis. shy specifies the shear factor along the y axis. | |
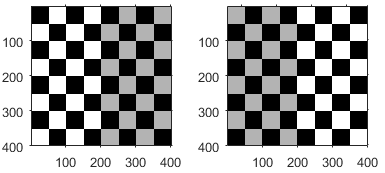
| Reflection |
| φ specifies the angle of the axis of reflection, in degrees. Two common reflections are vertical and horizontal reflection. Vertical reflection is reflection about the x-axis, so φ is 0 and the reflection matrix simplifies to:
Horizontal reflection is reflection about the y-axis, so φ is 90 and the reflection matrix simplifies to:
| |
| Rotation |
| θ specifies the angle of rotation about the origin, in degrees. | |
2-D Projective Transformations
Projective transformation enables the plane of the image to tilt. Parallel lines can converge towards a vanishing point, creating the appearance of depth.
The transformation is a 3-by-3 matrix. Unlike affine transformations, there are no
restrictions on the last row of the transformation matrix. Use any composition of 2-D affine
and projective transformation matrices to create a projtform2d
object representing a general projective transformation.
| 2-D Projective Transformation | Example | Transformation Matrix | |
|---|---|---|---|
| Tilt |
|
| E and F influence the vanishing point. When E and F are large, the vanishing point comes closer to the origin and thus parallel lines appear to converge more quickly. |
3-D Affine Transformations
The table lists the 3-D affine transformations with the transformation matrix used to
define them. Note that in the 3-D case, there are multiple matrices, depending on how you
want to rotate or shear the image. For 3-D affine transformations, the last row must be
[0 0 0 1].
Use combinations of 3-D translation matrices to create a
transltform3dobject representing a translation transformation.Use combinations of 3-D translation and rotation matrices to create a
rigidtform3dobject representing a nonreflective rigid transformation.Use combinations of 3-D translation, rotation, and scaling matrices to create a
simtform3dobject representing a nonreflective similarity transformation.Use any combination of 3-D transformation matrices to create an
affinetform3dobject representing a general affine transformation.
| 3-D Affine Transformation | Transformation Matrix | ||
|---|---|---|---|
| Translation | Translation by amount tx, ty, and tz in the x, y, and z directions, respectively:
| ||
| Scale | Scale by scale factor sx, sy, and sz in the x, y, and z dimensions, respectively:
| ||
| Shear | Shear within the y-z plane:
such that
| Shear within the x-z plane:
such that
| Shear within the x-y plane:
such that
|
| Reflection | Reflection across the y-z plane, negating the x coordinate:
| Reflection across the x-z plane, negating the y coordinate:
| Reflection across the x-y plane, negating the z coordinate:
|
| Rotation | Rotation within the y-z plane, by angle θx about the x axis, in degrees:
| Rotation within the x-z plane, by angle θy about the y axis, in degrees:
| Rotation within the x-y plane, by angle θz about the z axis, in degrees:
|
3-D Projective and N-D Transformations
The imwarp function does not support 3-D
projective transformations or N-D affine and projective transformations. Instead, you can
create a spatial transformation structure from a geometric transformation matrix using the
maketform function. Then, apply the
transformation to an image using the tformarray function. For more information, see N-Dimensional Spatial Transformations.
The dimensions of the transformation matrix must be (N+1)-by-(N+1). The
maketform and tformarray functions use the
postmultiply matrix convention. Geometric transformation matrices in the postmultiply
convention are the transpose of matrices in the premultiply convention. Therefore, for N-D
affine transformation matrices, the last column must contain [zeros(N,1);
1] and there are no restrictions on the values of the last row.
See Also
imwarp | fitgeotform2d | affinetform2d | affinetform3d | projtform2d