Overview of Filter Banks

A digital filter bank is an array of digital bandpass filters with either a common input or a common output. A filter bank can be an analysis filter bank with a series of analysis filters, or a synthesis filter bank with a series of synthesis filters. The analysis filter bank separates the input broadband signal x[n] into multiple components, each carrying a subband of the original signal. The synthesis filter bank merges these subbands into a single broadband signal, a reconstructed version of the original input signal.

Schematic of analysis filter bank on left followed by synthesis filter bank on right.

Analysis Filter Bank (Channelizer)

The generic analysis filter bank, also known as the channelizer, consists of a series of parallel bandpass filters that split an input broadband signal, x[n], into a series of narrow subbands. Each bandpass filter retains a different portion of the input signal. After the bandwidth is reduced by one of the bandpass filters, the signal is downsampled to a lower sample rate commensurate with the new bandwidth.

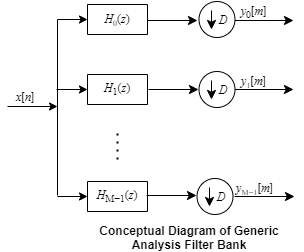
Conceptual diagram of generic analysis filter bank. The structure contains M branches. Each branch contains a filter followed by a downsampler.

The first branch in the filter bank contains a lowpass filter, H₀(z), which acts as a prototype filter. The remaining filters H₁(z) through H_M−1(z) are modulated versions of this filter. These modulated versions can be rearranged in terms of a complex exponential (modulation factor) followed by the prototype lowpass filter H₀(z).

Each branch contains a complex exponential followed by a prototype lowpass filter followed by a downsampler.

y₁[m], y₂[m], …, y_M-1[m] are narrow subband signals translated into baseband.

For more details on this structure, see Analysis Filter Bank.

This filter bank can be implemented efficiently using a polyphase structure. For more details on the polyphase structure and how it is implemented in the dsp.Channelizer object and the Channelizer block, see Channelizer Algorithm. The chief advantage of this polyphase implementation is that you can downsample the signal prior to filtering, thereby allowing you to filter the signal at a lower sample rate.

Synthesis Filter Bank (Channel synthesizer)

The synthesis filter bank, also known as the channel synthesizer, consists of a set of parallel bandpass filters that merge multiple input narrowband signals, y₀[m], y₁[m], y₂[m], … , y_M-1[m] into a single broadband signal, v[n]. The input narrowband signals are in the baseband. Each narrowband signal is interpolated to a higher sample rate by using the upsampler, and then filtered by the lowpass filter. A complex exponential that follows the lowpass filter centers the baseband signal around w_k, where $w_{k} = 2 π k / M$ and $k = 0, 1, 2, ..., M - 1$ .

Conceptual diagram of synthesis filter bank. Contains M branches. Each branch contains an upsampler, followed by a lowpass filter followed by a complex exponential. The output from each branch is added to form the reconstructed signal v[n].

This filter bank is implemented efficiently using the polyphase structure described in Channel Synthesizer Algorithm. The dsp.ChannelSynthesizer object and the Channel Synthesizer block in DSP System Toolbox™ use this implementation.

Two-Channel (Halfband) Filter Bank

Two-channel filter bank is a special case of the generic M-channel filter bank, where the number of filter branches is two.

The DFT matrix of the analysis portion looks like the following matrix.

$[\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}]$

The first row adds the two polyphase branches to give the lowpass subband output. The second row subtracts the two polyphase branches to give the highpass subband output. The halfband decimator objects and blocks in DSP System Toolbox implement their algorithm as shown in this diagram. A₀(z) and A₁(z) are the allpass polyphase components. This structure is the analysis portion of the two-channel halfband filter bank. Due to the halfband nature of the filters, one of the branches in this polyphase structure becomes a pure delay component.

Analysis portion of the two-channel filter bank. Switch at the input operates at a sample rate of fs. First branch contains A0(z) and second branch contains A1(z). Outputs from both filters are added to form the lowpass output on the first branch. Outputs from both filters are subtracted to from the highpass output on the second branch. Output sample rate is fs/2.

For more details on this structure and its derivation, see Polyphase Implementation under Algorithms on these reference pages.

Two-Channel Filter Bank	MATLAB^®	Simulink^®
Analysis portion using FIR halfband filter	`dsp.FIRHalfbandDecimator`	FIR Halfband Decimator
Analysis portion using IIR halfband filter	`dsp.IIRHalfbandDecimator`	IIR Halfband Decimator

Similarly, the halfband interpolator objects and blocks in DSP System Toolbox implement their algorithm as shown in this diagram. This structure is the synthesis portion of the two-channel halfband filter bank. Due to the halfband nature of the filters, one of the branches in this polyphase structure becomes a pure delay component.

Synthesis portion of the two-channel filter bank. Receives the lowpass and highpass subbands. First branch subtracts these two inputs and passes to A0(z). Second branch adds these two inputs and passes to A1(z). Outputs of A0(z) and A1(z) are sampled at a rate of fs using an output switch.

For more details on this structure and its derivation, see Polyphase Implementation under Algorithms on these reference pages.

Two-Channel Filter Bank	MATLAB	Simulink
Synthesis portion using FIR halfband filter	`dsp.FIRHalfbandInterpolator`	FIR Halfband Interpolator
Synthesis portion using IIR halfband filter	`dsp.IIRHalfbandInterpolator`	IIR Halfband Interpolator

The other two-channel filter bank features that DSP System Toolbox offers let you specify the lowpass and highpass filter coefficients. These features can customize the partitioning of the broadband signal. For an example, see Reconstruction Through Two-Channel Filter Banks.

Two-Channel Filter Bank	MATLAB	Simulink
Analysis filter bank	`dsp.SubbandAnalysisFilter`	Two-Channel Analysis Subband Filter
Synthesis filter bank	`dsp.SubbandSynthesisFilter`	Two-Channel Synthesis Subband Filter

You can use the subband analysis and synthesis filter banks as basic units and create multilevel filter banks. For more details, see Multilevel Filter Banks.

External Websites

Filter Bank Method: A Better Approach to Spectral Analysis