Levinson-Durbin

Solve linear system of equations using Levinson-Durbin recursion

• 

Libraries:
DSP System Toolbox / Estimation / Linear Prediction / Linear System Solvers
DSP System Toolbox / Math Functions / Matrices and Linear Algebra / Linear System Solvers

Description

The Levinson-Durbin block solves the nth-order system of linear equations

Ra = b

in the cases where:

• R is a Hermitian, positive-definite, Toeplitz matrix.

• b is identical to the first column of R shifted by one element and with the opposite sign.

$$\left[\begin{array}{cccc}r(1)& r^{*}(2)& \cdots & r^{*}(n)\\ r(2)& r(1)& \cdots & r^{*}(n-1)\\ ⋮& ⋮& \ddots & ⋮\\ r(n)& r(n-1)& \cdots & r(1)\end{array}\right]\left[\begin{array}{c}a(2)\\ a(3)\\ ⋮\\ a(n+1)\end{array}\right]=\left[\begin{array}{c}-r(2)\\ -r(3)\\ ⋮\\ -r(n+1)\end{array}\right]$$

Examples

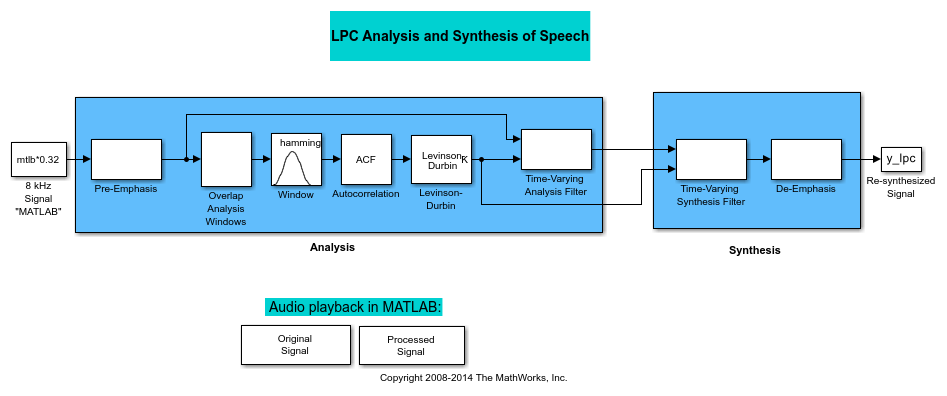
Analysis and Synthesis of Speech

A speech signal is usually represented in digital format, which is a sequence of binary bits. For storage and transmission applications, it is desirable to compress a signal by representing it with as few bits as possible, while maintaining its perceptual quality. Quantization is the process of representing a signal with a reduced level of precision. If you decrease the number of bits allocated for the quantization of your speech signal, the signal is distorted and the speech quality degrades.

• Open Model

Ports

Input

Input — Input

vector | matrix

Specify the input to the block, r = [r(1) r(2) ... r(n+1)] as a vector or a matrix. If the input is a matrix, the block treats each column as an independent channel and solves it separately. Each channel of the input contains lags 0 through n of an autocorrelation sequence, which appear in the matrix R.

If the input is fixed point, it must be a signed integer or a signed fixed point value with a power-of-two slope and zero bias.

Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes

Output

A — Model coefficients

vector | matrix

Model coefficients A, returned as a vector or a matrix. A has the same dimension as the input.

For each channel, port A outputs A = [1 a(2) a(3) ... a(n+1)], the solution to the Levinson-Durbin equation. You can also view the elements of each output channel as the coefficients of an nth-order autoregressive (AR) process.

Dependencies

To enable this port, set Output(s) to A and K or A.

Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes

K — Reflection coefficients

vector | matrix

Reflection coefficients K, returned as a vector or a matrix. K has the same dimension as the input, less one element.

For each channel, port K outputs K = [k(1) k(2) ... k(n)], which contains n reflection coefficients.

A scalar input channel causes an error when you select K. You can use reflection coefficients to realize a lattice representation of the AR process. For more details, see Applications.

Dependencies

To enable this port, set Output(s) to A and K or K.

Data Types: single | double | int8 | int16 | int32 | fixed point
Complex Number Support: Yes

P — Output prediction error power

vector

Output prediction error power P, returned as vector of length equal to the number of input channels. Each element in the vector is the prediction error power for each channel.

For each channel, P represents the power of the output of an FIR filter with taps A and input autocorrelation described by r, where A represents a prediction error filter and r is the input to the block. In this case, A is a whitening filter. P has one element per input channel.

Dependencies

To enable this port, select the Output prediction error power (P) check box.

Data Types: single | double | int8 | int16 | int32 | fixed point

Parameters

Main Tab

Output(s) — Output(s)

K (default) | A and K | A

Specify the solution representation of Ra = b to output:

• Polynomial coefficients (A) –– For each channel, port A outputs A = [1 a(2) a(3) ... a(n+1)], the solution to the Levinson-Durbin equation. A has the same dimension as the input. You can also view the elements of each output channel as the coefficients of an nth-order autoregressive (AR) process.

• Reflection coefficients (K) –– For each channel, port K outputs K = [k(1) k(2) ... k(n)], which contains n reflection coefficients and has the same dimension as the input, less one element. A scalar input channel causes an error when you select K. You can use reflection coefficients to realize a lattice representation of the AR process described later in this page.

• Both model coefficients and reflection coefficients (A and K) –– The block outputs both representations at their respective ports. A scalar input channel causes an error when you select A and K.

When the input is a scalar or row vector, you must set this parameter to A.

Output prediction error power (P) — Output prediction error power

off (default) | on

Select this parameter to output the prediction error power for each channel at port P.

If the value of lag 0 is zero, A=[1 zeros], K=[zeros], P=0 — If the value of lag 0 is zero, A=[1 zeros], K=[zeros], P=0

on (default) | off

When you select this check box and the first element of the input, r(1), is zero, the block outputs the following vectors, as appropriate:

• A = [1 zeros(1,n)]

• K = [zeros(1,n)]

• P = 0

When you clear this check box, the block outputs a vector of NaNs for each channel whose r(1) element is zero. In general, an input with r(1) = 0 is invalid because it does not construct a positive-definite matrix R. Often, however, blocks receive zero-valued inputs at the start of a simulation. The check box allows you to avoid propagating NaNs during this period.

Data Types Tab

Note

Floating-point inheritance takes precedence over the data type settings defined on this pane. When inputs are floating point, the block ignores these settings, and all internal data types are floating point.

Rounding mode — Rounding mode

Floor (default) | Ceiling | Convergent | Nearest | Round | Simplest | Zero

Specify the rounding mode for fixed-point operations as one of the following:

• Floor

• Ceiling

• Convergent

• Nearest

• Round

• Simplest

• Zero

For more details, see rounding mode.

Saturate on integer overflow — Saturate on integer overflow

off (default) | on

When you select this parameter, the block saturates the result of its fixed-point operation. When you clear this parameter, the block wraps the result of its fixed-point operation. For details on saturate and wrap, see overflow mode for fixed-point operations.

Product output — Product output

Inherit: Same as input (default) | numeric type

Specify the product output data type as Inherit: Same as input or a numeric type. See Fixed-Point Data Types and Multiplication Data Types for illustrations depicting the use of the product output data type in this block. You can set it to:

• A rule that inherits a data type, for example, Inherit: Same as input

• An expression that evaluates to a valid data type, for example, fixdt(1,16,0)

Click the Show data type assistant button to display the Data Type Assistant, which helps you set the Product output parameter.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

Accumulator — Accumulator

Inherit: Same as input (default) | Inherit: Same as product output | numeric type

Specify the accumulator data type as Inherit: Same as input, Inherit: Same as product output, or a numeric type. See Fixed-Point Data Types for illustrations depicting the use of the accumulator data type in this block. You can set it to:

• A rule that inherits a data type, for example, Inherit: Same as input

• A rule that inherits a data type, for example, Inherit: Same as product output

• An expression that evaluates to a valid data type, for example, fixdt(1,16,0)

Click the Show data type assistant button to display the Data Type Assistant, which helps you set the Accumulator parameter.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

Polynomial coefficients (A) — Polynomial coefficients data type

fixdt(1,16,0) (default) | numeric type

Specify the polynomial coefficients (A) data type as a numeric type. See Fixed-Point Data Types for illustrations depicting the use of the A data type in this block. You can set it to an expression that evaluates to a valid data type, for example, fixdt(1,16,10).

Click the Show data type assistant button to display the Data Type Assistant, which helps you set the A parameter.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

Reflection coefficients (K) — Reflection coefficients data type

fixdt(1,16,0) (default) | numeric type

Specify the reflection coefficients (K) data type as a numeric type. See Fixed-Point Data Types for illustrations depicting the use of the K data type in this block. You can set it to an expression that evaluates to a valid data type, for example, fixdt(1,16,10).

Click the Show data type assistant button to display the Data Type Assistant, which helps you set the K parameter.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

Prediction error power (P) — Prediction error power data type

Inherit: Same as input (default) | numeric type

Specify the prediction error power (P) data type as Inherit: Same as input or a numeric type. See Fixed-Point Data Types for illustrations depicting the use of the P data type in this block. You can set it to:

• A rule that inherits a data type, for example, Inherit: Same as input

• An expression that evaluates to a valid data type, for example, fixdt(1,16,0)

Click the Show data type assistant button to display the Data Type Assistant, which helps you set the P parameter.

See Specify Data Types Using Data Type Assistant (Simulink) for more information.

Minimum — Minimum values of polynomial coefficients, reflection coefficients, or prediction error power

[] (default) | scalar

Specify the minimum values that the polynomial coefficients, reflection coefficients, or prediction error power should have. The default value is [] (unspecified). Simulink^® uses this value to perform:

• Parameter range checking (see Specify Minimum and Maximum Values for Block Parameters (Simulink))

• Automatic scaling of fixed-point data types

Maximum — Maximum values of polynomial coefficients, reflection coefficients, or prediction error power

[] (default) | scalar

Specify the maximum values that the polynomial coefficients, reflection coefficients, or prediction error power should have. The default value is [] (unspecified). Simulink uses this value to perform:

• Parameter range checking (see Specify Minimum and Maximum Values for Block Parameters (Simulink))

• Automatic scaling of fixed-point data types

Lock data type settings against changes by the fixed-point tools — Prevent fixed-point tools from overriding data types

off (default) | on

Select this parameter to prevent the fixed-point tools from overriding the data types you specify in the block dialog box.

Block Characteristics

Data Types	double | fixed point | integer | single
Direct Feedthrough	no
Multidimensional Signals	no
Variable-Size Signals	no
Zero-Crossing Detection	no

More About

Fixed-Point Data Types

The diagrams in this section show the data types used within the Levinson-Durbin block for fixed-point signals.

After initialization the block performs n updates. At the (j+1) update,

$$\text{value in accumulator }=r(j+1)+{\displaystyle \sum a_j(i)\times r\left(j-i+1\right)}$$

The following diagram displays the fixed-point data types used in this calculation:

The block then updates the reflection coefficients K according to

$$K_{j+1}=\text{ value in accumulator}/P_j$$

The block then updates the prediction error power P according to

$$P_{j+1}=P_j-P_j\times K_{j+1}\times \text{conj}\left(K_{j+1}\right)$$

The next diagram displays the fixed-point data types used in this calculation:

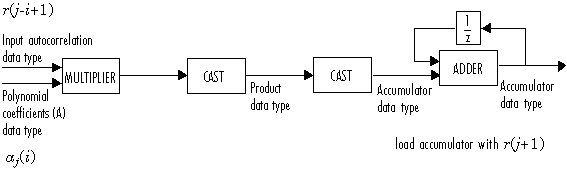
The polynomial coefficients A are then updated according to

$$a_{j+1}(i)=a_j(i)+K_{j+1}\times \text{conj}\left({\text{a}}_{\text{j}}(j-1+i)\right)$$

This diagram displays the fixed-point data types used in this calculation:

Applications

One application of the Levinson-Durbin formulation implemented by this block is in the Yule-Walker AR problem, which concerns modeling an unknown system as an autoregressive process. You would model such a process as the output of an all-pole IIR filter with white Gaussian noise input. In the Yule-Walker problem, the use of the signal's autocorrelation sequence to obtain an optimal estimate leads to an Ra = b equation of the type shown above, which is most efficiently solved by Levinson-Durbin recursion. In this case, the input to the block represents the autocorrelation sequence, with r(1) being the zero-lag value. The output at the block's A port then contains the coefficients of the autoregressive process that optimally models the system. The coefficients are ordered in descending powers of z, and the AR process is minimum phase. The prediction error, G, defines the gain for the unknown system, where $$G=\sqrt{P}$$:

$$H\left(z\right)=\frac{G}{A(z)}=\frac{G}{1+a(2)z^{-1}+\mathrm{...}+a(n+1)z^{-n}}$$

The output at the block's K port contains the corresponding reflection coefficients, [k(1) k(2) ... k(n)], for the lattice realization of this IIR filter. The Yule-Walker AR Estimator block implements this autocorrelation-based method for AR model estimation, while the Yule-Walker Method block extends the method to spectral estimation.

Another common application of the Levinson-Durbin algorithm is in linear predictive coding, which is concerned with finding the coefficients of a moving average (MA) process (or FIR filter) that predicts the next value of a signal from the current signal sample and a finite number of past samples. In this case, the input to the block represents the signal's autocorrelation sequence, with r(1) being the zero-lag value, and the output at the block's A port contains the coefficients of the predictive MA process (in descending powers of z).

$$H\left(z\right)=A\left(z\right)=1+a(2)z^{-1}+\mathrm{...}a(n+1)z^{-n}$$

These coefficients solve the following optimization problem:

$$\stackrel{\min }{\left\{a_i\right\}}$$

$$E\left[{\left|x_n-{\displaystyle \sum _{i=1}^N{a}_i{x}_{n-i}}\right|}^2\right]$$

Again, the output at the block's K port contains the corresponding reflection coefficients, [k(1) k(2) ... k(n)], for the lattice realization of this FIR filter. The Autocorrelation LPC block in the Linear Prediction library implements this autocorrelation-based prediction method.

Algorithms

The algorithm requires O(n²) operations for each input channel. This implementation is therefore much more efficient for large n than standard Gaussian elimination, which requires O(n³) operations per channel.

References

[1] Golub, G. H. and C. F. Van Loan. Sect. 4.7 in Matrix Computations. 3rd ed. Baltimore, MD: Johns Hopkins University Press, 1996.

[2] Ljung, L. System Identification: Theory for the User. Englewood Cliffs, NJ: Prentice Hall, 1987. Pgs. 278–280.

[3] Kay, Steven M. Modern Spectral Estimation: Theory and Application. Englewood Cliffs, NJ: Prentice Hall, 1988.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

Generated code relies on the memcpy or memset function (string.h) under certain conditions.

Version History

Introduced before R2006a