iirlp2mbc
Transform IIR lowpass filter to IIR complex multiband filter
Description
[
transform an IIR lowpass filter to an IIR complex multiband filter.num,den,allpassNum,allpassDen] =
iirlp2mbc(b,a,wo,wt)
The iirlp2mbc returns the numerator and denominator
coefficients of the transformed complex IIR multiband filter. The function also
returns the numerator, allpassNum, and the denominator,
allpassDen, of the
Mth order allpass mapping filter.
The prototype lowpass filter is specified with the numerator b
and the denominator a.
The function transforms a real lowpass prototype filter to a multiband filter by applying an Mth-order real lowpass to complex multiple bandpass frequency mapping. Parameter M is the number of times an original feature is replicated in the transformed filter. For more details, see IIR Lowpass Filter to IIR Complex Multiband Filter Transformation.
Examples
Transform a real lowpass IIR filter to a complex multiband IIR filter using the iirlp2mbc function.
Input Lowpass IIR Filter
Design a prototype real IIR lowpass elliptic filter with a gain of about –3 dB at 0.5π rad/sample.
[b,a] = ellip(3,0.1,30,0.409); filterAnalyzer(b,a)

Transform Filter Using iirlp2mbc
Transform the real prototype lowpass filter into a complex multiband filter with two passbands.
Specify the prototype filter as a vector of numerator and denominator coefficients, b and a respectively.
[num,den] = iirlp2mbc(b,a,0.5,[-7 -5 6 8]/10);
Compare the magnitude response of the filters. iirlp2mbc replicates the desired feature at 0.5 in the lowpass filter at four locations in the multiband filter.
filterAnalyzer(b,a,num,den,FrequencyRange="centered",... FilterNames=["PrototypeFilter_TFForm",... "TransformedMultibandFilter"])

Alternatively, you can also specify the input lowpass IIR filter as a matrix of coefficients. Pass the second-order section matrices as inputs. The transformed filter is a fourth-order section filter given by the numerator and the denominator coefficients num2 and den2.
ss = tf2sos(b,a); [num2,den2] = iirlp2mbc(ss(:,1:3),ss(:,4:6),0.5,[-7 -5 6 8]/10);
To visualize the magnitude response of the fourth-order section filter, first pass the filter coefficients to the dsp.FourthOrderSectionFilter object. Then, use this object as an input to the filter analyzer.
fos = dsp.FourthOrderSectionFilter(Numerator=num2,...
Denominator=den2);Use the sos2ctf function to convert the second-order section matrices to the cascaded transfer function form.
[b_ctf,a_ctf] = sos2ctf(ss);
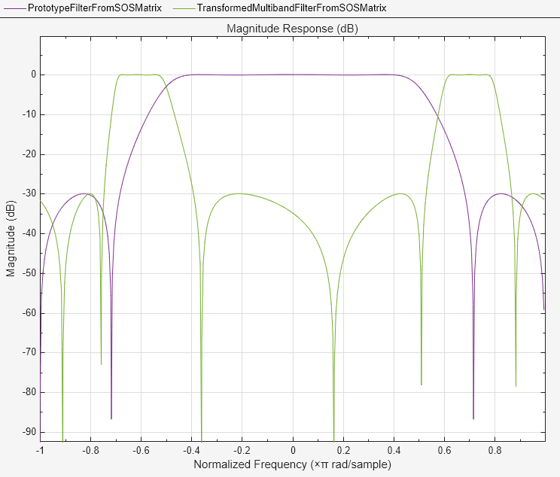
Compare the magnitude response of the filters.
filterAnalyzer(b_ctf,a_ctf,fos,FrequencyRange="centered",... FilterNames=["PrototypeFilterFromSOSMatrix",... "TransformedMultibandFilterFromSOSMatrix"]);
Copyright 2012–2024 The MathWorks, Inc.
Input Arguments
Numerator coefficients of the prototype lowpass IIR filter, specified as either:
Row vector –– Specifies the values of [b0, b1, …, bn], given this transfer function form:
where n is the order of the filter.
Matrix –– Specifies the numerator coefficients in the form of an P-by-(Q+1) matrix, where P is the number of filter sections and Q is the order of each filter section. If Q = 2, the filter is a second-order section filter. For higher-order sections, make Q > 2.
In the transfer function form, the numerator coefficient matrix bik of the IIR filter can be represented using the following equation:
where,
a –– Denominator coefficients matrix. For more information on how to specify this matrix, see
a.k –– Row index.
i –– Column index.
When specified in the matrix form, b and a matrices must have the same number of rows (filter sections) Q.
Data Types: single | double
Complex Number Support: Yes
Denominator coefficients for a prototype lowpass IIR filter, specified as one of these options:
Row vector –– Specifies the values of [a0, a1, …, an], given this transfer function form:
where n is the order of the filter.
Matrix –– Specifies the denominator coefficients in the form of an P-by-(Q+1) matrix, where P is the number of filter sections and Q is the order of each filter section. If Q = 2, the filter is a second-order section filter. For higher-order sections, make Q > 2.
In the transfer function form, the denominator coefficient matrix aik of the IIR filter can be represented using the following equation:
where,
b –– Numerator coefficients matrix. For more information on how to specify this matrix, see
b.k –– Row index.
i –– Column index.
When specified in the matrix form, a and b matrices must have the same number of rows (filter sections) P.
Data Types: single | double
Complex Number Support: Yes
Frequency value to transform from the prototype filter, specified as a
positive scalar. Frequency wo should be normalized to be
between 0 and 1, with
1 corresponding to half the sample rate.
Data Types: single | double
Desired frequency locations in the transformed target filter, specified as
a row vector. Frequencies in wt should be normalized to
be between -1 and 1, with
1 corresponding to half the sample rate. The value of
M which is equal to the number of times an original
feature is replicated in the transformed filter equals the length of the
wt vector.
Data Types: single | double
Output Arguments
Numerator coefficients of the transformed multiband filter, returned as one of the following:
Row vector of length Mn/2+1, where M is the number of times an original feature is replicated in the transformed filter and n is the order of the input filter. The value of M equals the length of the
wtvector.The
numoutput is a row vector when the input coefficientsbandaare row vectors.P-by-(QM/2+1) matrix, where P is the number of filter sections, Q is the order of each section of the transformed filter, and M is the number of times an original feature is replicated in the transformed filter.
The
numoutput is a matrix when the input coefficientsbandaare matrices.
Data Types: single | double
Complex Number Support: Yes
Denominator coefficients of the transformed multiband filter, returned as one of the following:
Row vector of length Mn/2+1, where M is the number of times an original feature is replicated in the transformed filter and n is the order of the input filter. The value of M equals the length of the
wtvector.The
denoutput is a row vector when the input coefficientsbandaare row vectors.P-by-(QM/2+1) matrix, where P is the number of filter sections, Q is the order of each section of the transformed filter, and M is the number of times an original feature is replicated in the transformed filter.
The
denoutput is a matrix when the input coefficientsbandaare matrices.
Data Types: single | double
Complex Number Support: Yes
Numerator coefficients of the mapping filter, returned as a row vector.
Data Types: single | double
Complex Number Support: Yes
Denominator coefficients of the mapping filter, returned as a row vector.
Data Types: single | double
Complex Number Support: Yes
More About
IIR lowpass filter to IIR complex multiband filter transformation
effectively places one feature of the original filter, located at frequency
wo, at the required target
frequency locations, wt1, …
,wtM.
Relative positions of other features of the original filter do not change in the target filter. This means that it is possible to select two features of an original filter, F1 and F2, with F1 preceding F2. Feature F1 will still precede F2 after the transformation. However, the distance between F1 and F2 will not be the same before and after the transformation.
Choice of the feature subject to this transformation is not restricted to the cutoff frequency of an original lowpass filter. You can choose to transform any feature of the original filter like stopband edge, DC, deep minimum in the stopband, or others.
The IIR lowpass filter to IIR complex multiband filter transformation can also be used for transforming other types of filters, for example, notch filters or resonators can be easily replicated at a number of required frequency locations. A good application would be an adaptive tone cancellation circuit reacting to the changing number and location of tones.
References
[1] Krukowski, A., and I. Kale. “High-Order Complex Frequency Transformations,” Internal report No. 27/2001. Applied DSP and VLSI Research Group, University of Westminster.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Version History
Introduced in R2011a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Website auswählen
Wählen Sie eine Website aus, um übersetzte Inhalte (sofern verfügbar) sowie lokale Veranstaltungen und Angebote anzuzeigen. Auf der Grundlage Ihres Standorts empfehlen wir Ihnen die folgende Auswahl: .
Sie können auch eine Website aus der folgenden Liste auswählen:
So erhalten Sie die bestmögliche Leistung auf der Website
Wählen Sie für die bestmögliche Website-Leistung die Website für China (auf Chinesisch oder Englisch). Andere landesspezifische Websites von MathWorks sind für Besuche von Ihrem Standort aus nicht optimiert.
Amerika
- América Latina (Español)
- Canada (English)
- United States (English)
Europa
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)