dsp.SampleRateConverter

Multistage sample rate converter

Description

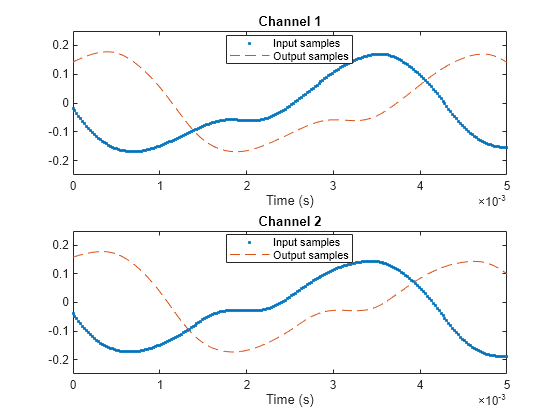
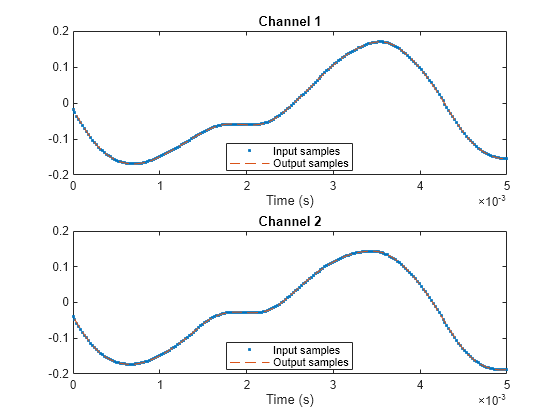
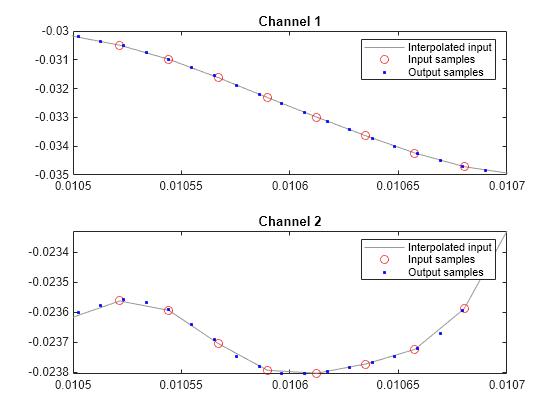
The SampleRateConverter System object™ converts the sample rate of an incoming signal.

To convert the sample rate of a signal:

1. Create the dsp.SampleRateConverter object and set its properties.

2. Call the object with arguments, as if it were a function.

To learn more about how System objects work, see What Are System Objects?

This object supports C/C++ code generation and SIMD code generation under certain conditions. For more information, see Code Generation.

Creation

Syntax

src = dsp.SampleRateConverter

src = dsp.SampleRateConverter(Name=Value)

Description

src = dsp.SampleRateConverter creates a multistage FIR sample rate converter System object, src, that converts the sample rate of each channel of an input signal.

src = dsp.SampleRateConverter(Name=Value) returns a multistage FIR sample rate converter System object, src, with properties and options specified by one or more Name-Value pair arguments.

Properties

Unless otherwise indicated, properties are nontunable, which means you cannot change their values after calling the object. Objects lock when you call them, and the release function unlocks them.

If a property is tunable, you can change its value at any time.

For more information on changing property values, see System Design in MATLAB Using System Objects.

Bandwidth — Two-sided bandwidth of interest

40000 (default) | positive scalar

Specify the two-sided bandwidth of interest (after rate conversion) as a positive scalar expressed in Hz. This property sets the two-sided bandwidth of the information-carrying portion of the signal that you wish to retain.

InputSampleRate — Sample rate of input signal

192000 (default) | positive scalar

Specify the sample rate of the input signal as a positive scalar expressed in Hz. The input sample rate must be greater than the bandwidth of interest.

OutputRateTolerance — Maximum allowed tolerance for output sample rate

0 (default) | positive scalar

Specify the maximum allowed tolerance for the sample rate of the output signal as a positive scalar between 0 and 1.

The output rate tolerance allows for a simpler design in many cases. The actual output sample rate varies but is within the specified range. For example, if OutputRateTolerance is specified as 0.01, then the actual output sample rate is in the range given by OutputSampleRate ± 1%.

OutputSampleRate — Sample rate of output signal

44100 (default) | positive scalar

Specify the sample rate of the output signal as a positive scalar expressed in Hz. The output sample rate must be greater than the bandwidth of interest.

StopbandAttenuation — Minimum dB attenuation for aliased components

80 (default) | positive scalar

Specify the stopband attenuation as a positive scalar expressed in dB. This property is the minimum amount by which any aliasing involved in the process is attenuated.

Usage

Syntax

y = src(x)

Description

y = src(x) designs one or more multirate FIR filters and then uses the filters to convert the rate of each channel (column) of the real or complex input signal x to the output sampling rate.

Input Arguments

x — Input signal

vector | matrix

Input signal, specified as a vector or a matrix of size P-by-Q. The number of input rows P can be arbitrary and does not have to be a multiple of the overall decimation factor. You can determine the decimation factor using the getRateChangeFactors function. The object treats each column of x as a separate channel.

This object supports variable-size input signals, that is, the frame length (number of rows) of the signal can change even when the object is locked. However, the number of channels (columns) must remain constant.

Data Types: single | double
Complex Number Support: Yes

Output Arguments

y — Resampled signal

vector | matrix

Resampled signal, returned as a vector or a matrix. The output frame size depends on the input frame size P and the rate conversion factors of the individual filter stages. For more information on these filter stages, use the getFilters function.

The number of output channels (columns) is the same as the number of input channels.

Data Types: single | double
Complex Number Support: Yes

Object Functions

To use an object function, specify the System object as the first input argument. For example, to release system resources of a System object named obj, use this syntax:

release(obj)

Specific to dsp.SampleRateConverter

getActualOutputRate	Get actual output rate
getFilters	Obtain single-stage filters
getRateChangeFactors	Get overall interpolation and decimation factors
visualize	Visualize filter stages

Filter Analysis

cost	Implementation cost of the sample rate converter
freqz	Frequency response of the multirate multistage filter
info	Display information about sample rate converter

Common to All System Objects

step	Run System object algorithm
release	Release resources and allow changes to System object property values and input characteristics
reset	Reset internal states of System object

Examples

Convert Sample Rate of Audio Signal

Convert the sample rate of an audio signal from 44.1 kHz (CD quality) to 96 kHz (DVD quality).

Note: The dsp.AudioFileWriter System object™ is not supported in MATLAB Online.

FsIn = 44.1e3;
FsOut = 96e3;

SRC = dsp.SampleRateConverter(Bandwidth=40e3,...
    InputSampleRate=FsIn,OutputSampleRate=FsOut);

[L,M] = getRateChangeFactors(SRC);
FrameSize = 10*M;

AR = dsp.AudioFileReader('guitar10min.ogg', ...
    SamplesPerFrame=FrameSize);
AW = dsp.AudioFileWriter('guitar10min_96k.wav', ...
    SampleRate=FsOut);

Convert 100 frames of audio signal. Release all objects.

for n = 1:100
    x = AR();
    y = SRC(x);
    AW(y);
end

release(AR);
release(AW);
release(SRC);

Plot the input and output signals. The latency of the sample rate converter introduces a delay in the output signal.

tx = (0:length(x)-1)./FsIn;
ty = (0:length(y)-1)./FsOut;
figure
subplot(2,1,1)
plot(tx,x(:,1),'.')
hold on
plot(ty,y(:,1),'--')
ylim([-0.25 0.25]);
xlim([0 0.005])
xlabel('Time (s)')
legend('Input samples','Output samples','Location','best')
title('Channel 1')
subplot(2,1,2)
plot(tx,x(:,2),'.')
hold on
plot(ty,y(:,2),'--')
ylim([-0.25 0.25]);
xlim([0 0.005])
xlabel('Time (s)')
legend('Input samples','Output samples','Location','best')
title('Channel 2')

Use the outputDelay function to determine this delay value. To account for this delay, shift the output by this delay value.

[delay,~,~] = outputDelay(SRC,Fc=0)

delay = 
0.0012

tx = (0:length(x)-1)./FsIn;
ty = (0:length(y)-1)./FsOut;
figure
subplot(2,1,1)
plot(tx,x(:,1),'.')
hold on
plot(ty-delay,y(:,1),'--')
xlim([0 0.005])
xlabel('Time (s)')
legend('Input samples','Output samples','Location','best')
title('Channel 1')
subplot(2,1,2)
plot(tx,x(:,2),'.')
hold on
plot(ty-delay,y(:,2),'--')
xlim([0 0.005])
xlabel('Time (s)')
legend('Input samples','Output samples','Location','best')
title('Channel 2')

Zoom in to see the difference in sample rates.

figure
subplot(2,1,1)
plot(tx,x(:,1),Color=[0.6 0.6 0.6])
hold on
plot(tx,x(:,1),'ro')
plot(ty-delay,y(:,1),'b.')
xlim([0.0105 0.0107])
legend('Interpolated input','Input samples','Output samples')
title('Channel 1')
subplot(2,1,2)
plot(tx,x(:,2),Color=[0.6 0.6 0.6])
hold on
plot(tx,x(:,2),'ro')
plot(ty-delay,y(:,2),'b.')
xlim([0.0105 0.0107])
legend('Interpolated input','Input samples','Output samples')
title('Channel 2')

Convert Sample Rate of Sinusoid

Create a multistage sample rate converter with default properties. The converter converts from 192 kHz to 44.1 kHz in three stages.

src = dsp.SampleRateConverter

src = 
  dsp.SampleRateConverter with properties:

        InputSampleRate: 192000
       OutputSampleRate: 44100
    OutputRateTolerance: 0
              Bandwidth: 40000
    StopbandAttenuation: 80

Use src to convert the sample rate of a noisy sinusoid. The sinusoid has a frequency of 20 kHz and is sampled for 0.1 s.

f = 20e3;

FsIn = src.InputSampleRate;
FsOut = src.OutputSampleRate;

t1 = (0:1/FsIn:0.1-1/FsIn)';

sIn = sin(2*pi*f*t1) + randn(size(t1));

Estimate the power spectral density of the input.

hsa = spectrumAnalyzer(SampleRate=FsIn,...
    Method='welch',YLimits=[-40 40]);
hsa(sIn)
release(hsa)

Convert the sample rate of the signal. Estimate the power spectral density of the output.

sOut = src(sIn);

hsb = spectrumAnalyzer(SampleRate=FsOut,...
    Method='welch',YLimits=[-40 40]);
hsb(sOut)
release(hsb)

Tolerance Cost in Sample Rate Conversion

A signal output from an A/D converter is sampled at 98.304 MHz. The signal has a bandwidth of 20 MHz. Reduce the sample rate of the signal to 22 MHz, which is the bandwidth of 802.11 channels. Make the conversion exactly and then redo it with an output rate tolerance of 1%.

SRC1 = dsp.SampleRateConverter(Bandwidth=20e6, ...
    InputSampleRate=98.304e6,OutputSampleRate=22e6, ...
    OutputRateTolerance=0);
SRC2 = dsp.SampleRateConverter(Bandwidth=20e6,...
    InputSampleRate=98.304e6,OutputSampleRate=22e6, ...
    OutputRateTolerance=0.01);

Use the cost method to determine the cost of each sample rate conversion. The zero-tolerance process requires more than 500 times as many coefficients as the 1% process.

c1 = cost(SRC1)

c1 = struct with fields:
                  NumCoefficients: 84779
                        NumStates: 133
    MultiplicationsPerInputSample: 27.0422
          AdditionsPerInputSample: 26.0684

c2 = cost(SRC2)

c2 = struct with fields:
                  NumCoefficients: 150
                        NumStates: 127
    MultiplicationsPerInputSample: 22.6667
          AdditionsPerInputSample: 22.1111

Find the integer upsampling and downsampling factors used in each conversion.

[L1,M1] = getRateChangeFactors(SRC1)

L1 = 
1375

M1 = 
6144

[L2,M2] = getRateChangeFactors(SRC2)

L2 = 
2

M2 = 
9

Compute the actual sample rate of the output signal when the sample rate conversion has a tolerance of 1%.

getActualOutputRate(SRC2)

ans = 
2.1845e+07

Reset a Sample Rate Converter

Create a multistage sample rate converter with default properties, corresponding to the combined three filter stages used to convert from 192 kHz to 44.1 kHz. Determine its overall decimation and interpolation factors.

src = dsp.SampleRateConverter;

[L,M] = getRateChangeFactors(src);

Create a two-channel random signal. Specify a number of samples equal to the decimation factor. Call the object twice on the signal.

x = randn(M,2);

y1 = src(x);
y2 = src(x);

no = all(y2==y1)

no = 1x2 logical array

   0   0

The output is different because the internal states of src have changed. Use reset to reset the converter and call the converter again. Verify that the output is unchanged.

reset(src)

y3 = src(x);

yes = all(y3==y1)

yes = 1x2 logical array

   1   1

Frequency Response of Default Converter

Create a multistage sample rate converter with default properties, corresponding to the combined three filter stages used to convert from 192 kHz to 44.1 kHz. Compute and display the frequency response.

src = dsp.SampleRateConverter;
[H,f] = freqz(src);
plot(f,20*log10(abs(H)))

Compute and display the frequency response over the range between 20 Hz and 44.1 kHz.

f = 20:10:44.1e3;
[H,f] = freqz(src,f);
plot(f,20*log10(abs(H)))

Single-Stage Filters

Create src, a multistage sample rate converter with default properties. src converts between 192 kHz and 44.1 kHz. Find the individual filters that are cascaded together to perform the conversion.

src = dsp.SampleRateConverter;
c = getFilters(src);

Visualize the frequency response of the decimator used in the first stage of the process.

m = c.Stage1;

[h,w] = freqz(m);
plot(w/pi,20*log10(abs(h)))
xlabel('\omega / \pi')
ylabel('Magnitude (dB)')

Default Multistage Sample Rate Converter

Create a multistage sample rate converter with default properties, corresponding to the combined three filter stages used to convert from 192 kHz to 44.1 kHz.

src = dsp.SampleRateConverter

src = 
  dsp.SampleRateConverter with properties:

        InputSampleRate: 192000
       OutputSampleRate: 44100
    OutputRateTolerance: 0
              Bandwidth: 40000
    StopbandAttenuation: 80

Display information about the design.

info(src)

ans = 
    'Overall Interpolation Factor    : 147
     Overall Decimation Factor       : 640
     Number of Filters               : 3
     Multiplications per Input Sample: 27.667188
     Number of Coefficients          : 8631
     Filters:                         
        Filter 1:
        dsp.FIRDecimator     - Decimation Factor   : 2 
        Filter 2:
        dsp.FIRDecimator     - Decimation Factor   : 2 
        Filter 3:
        dsp.FIRRateConverter - Interpolation Factor: 147
                             - Decimation Factor   : 160 
     '

Output Sample Rate with Given Tolerance

Get the actual output sample rate for conversion between 192 kHz and 44.1 kHz when given a tolerance of 1%.

src = dsp.SampleRateConverter;
src.OutputRateTolerance = 0.01;
FsOut = getActualOutputRate(src)

FsOut = 
4.4308e+04

Default Resampling Factors

Create src, a multistage sample rate converter with default properties. src combines three filter stages to convert from 192 kHz to 44.1 kHz. Determine its overall interpolation and decimation factors.

src = dsp.SampleRateConverter;
[L,M] = getRateChangeFactors(src)

L = 
147

M = 
640

Sample Rate Converter Stages

Create a multistage sample rate converter with default properties, corresponding to the combined three filter stages used to convert from 192 kHz to 44.1 kHz. Visualize the stages.

src = dsp.SampleRateConverter;
visualize(src)

Algorithms

• The general multistage sample rate converter performs a multistage decimation, a single-stage sample rate conversion, and a multistage interpolation. Actual designs include at most two of these steps.

• The procedure automatically determines the optimal number of decimation or interpolation stages. In special cases, the algorithm can perform a decimation or interpolation in a single stage.

• The algorithm always attempts to start by reducing the sample rate. This decreases the amount of computation required. The decimation step ensures that the intermediate sample rate does not go below the bandwidth of interest and that the block does not filter out any information.

• Each individual stage uses halfband or Nyquist filters to minimize the number of nonzero coefficients.

• The algorithm allows transition-band aliasing because it decreases the implementation cost. It keeps the signal within the bandwidth of interest alias free up to the value specified by the StopbandAttenuation property.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using MATLAB® Coder™.

Usage notes and limitations:

• See System Objects in MATLAB Code Generation (MATLAB Coder).

• The getRateChangeFactors function supports C and C++ code generation.

• This object supports SIMD code generation using Intel^® AVX2 code replacement library under these conditions:

  • For upsampling, the ratio of output sample rate to input sample rate must be an integer.

  • For downsampling, the ratio of input sample rate to output sample rate must be an integer.

  • Input signal has a data type of single or double.

  The SIMD technology significantly improves the performance of the generated code. For more information, see SIMD Code Generation. To generate SIMD code from this object, see Use Intel AVX2 Code Replacement Library to Generate SIMD Code from MATLAB Algorithms.

• In the code you generate from this object, the resampled signal output is a fixed-size signal if the input signal is fixed size and is a multiple of the decimation factor. If the input is not a multiple of the decimation factor or if the input is a variable-size signal, then the resampled signal output is of variable-size.

Version History

Introduced in R2014b

R2024b: visualizeFilterStages has been renamed to visualize

The visualizeFilterStages function has been renamed to visualize. Existing instances of this function continue to run. For new instances, use visualize.

R2024b: visualize launches MATLAB figure

The visualize function now launches a MATLAB^® figure to visualize the filter stages of the sample rate converter.

R2023a: Support for arbitrary input frame length

This object supports an input signal with an arbitrary frame length, so the input frame length does not have to be a multiple of the decimation factor.