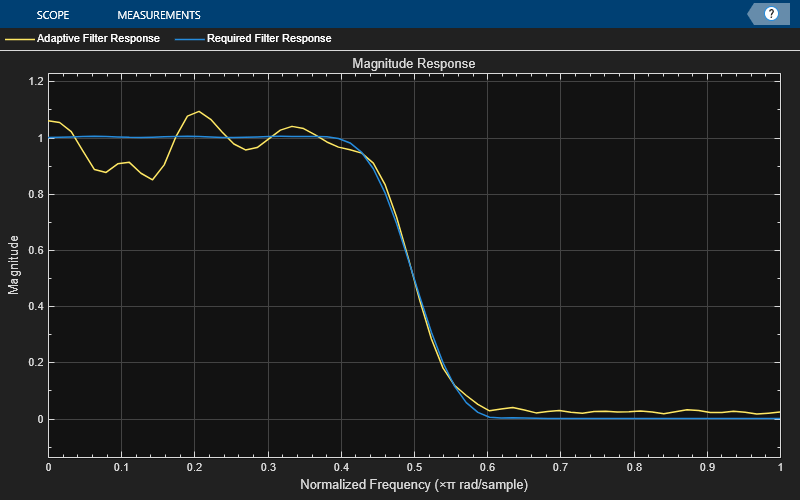
Adaptive Filter
DSP System Toolbox™ umfasst mehrere Varianten der adaptiven LMS- und RLS-FIR-Filteralgorithmen (FIR: Finite Impulse Response). Diese Algorithmen unterscheiden sich im Detail, weisen jedoch einen gemeinsamen operativen Ansatz auf, bei dem die Fehlerdifferenz zwischen der adaptiven Filterausgabe und dem gewünschten Signal minimiert wird. Die MSE-Methode (mittleres Fehlerquadrat) ist die gebräuchlichste Metrik zur Quantifizierung dieses Fehlers. Adaptive Filter werden in zahlreichen Anwendungen eingesetzt, darunter akustische Rauschunterdrückung, Echo-Unterdrückung, Strahlformen, Systemidentifikation, biomedizinische Signalverstärkung, Entzerrung von Kommunikationskanälen usw. Beispiele zu einigen dieser Anwendungen finden Sie unter System Identification of FIR Filter Using LMS Algorithm, Noise Cancellation Using Sign-Data LMS Algorithm und Inverse System Identification Using RLS Algorithm.
Bei farbigen Eingaben bieten die adaptiven Affine-Projection-Filteralgorithmen des dsp.AffineProjectionFilter-Objekts eine erheblich bessere Konvergenzgeschwindigkeit als die LMS-Filtervarianten. Für höheren Rechenaufwand bieten die adaptiven Lattice-Filteralgorithmen des dsp.AdaptiveLatticeFilter-Objekts eine bessere Konvergenz als die LMS- und RLS-Filter. Mithilfe des dsp.FrequencyDomainAdaptiveFilter-Objekts können Sie zudem einen adaptiven FIR-Filter in der Frequenzdomäne implementieren.
Die Konvergenzleistung wird durch die Trajektorie des Ist-MSE festgelegt, ermittelt durch msesim, und die Konvergenz mit dem prognostizierten MSE, ermittelt durch msepred.
Objekte
dsp.BlockLMSFilter | Compute output, error, and weights using block least mean squares (LMS) adaptive algorithm |
dsp.LMSFilter | Compute output, error, and weights of least mean squares (LMS) adaptive filter |
dsp.RLSFilter | Compute output, error and coefficients using recursive least squares (RLS) algorithm |
dsp.AffineProjectionFilter | Compute output, error and coefficients using affine projection (AP) Algorithm |
dsp.AdaptiveLatticeFilter | Adaptive lattice filter |
dsp.FastTransversalFilter | Fast transversal least-squares FIR adaptive filter |
dsp.FilteredXLMSFilter | Filtered XLMS filter |
dsp.FrequencyDomainAdaptiveFilter | Compute output, error, and coefficients using frequency-domain FIR adaptive filter |
Blöcke
| Block LMS Filter | Compute output, error, and weights using LMS adaptive algorithm |
| Fast Block LMS Filter | Compute output, error, and weights using least mean squares (LMS) adaptive algorithm |
| Frequency-Domain Adaptive Filter | Compute output, error, and coefficients using frequency domain FIR adaptive filter |
| Kalman Filter | Predict or estimate states of dynamic systems |
| LMS Filter | Compute output, error, and weights using least mean squares (LMS) adaptive algorithm |
| LMS Update | Estimate weights of least mean squares (LMS) adaptive filter |
| RLS Filter | Compute filtered output, filter error, and filter weights for given input and desired signal using RLS adaptive filter algorithm |
Themen
- Overview of Adaptive Filters and Applications
General discussion on how adaptive filters work, list of adaptive filter algorithms in DSP System Toolbox, convergence performance, and details on few common applications.
- System Identification of FIR Filter Using LMS Algorithm
Identify an unknown system using LMS algorithm.
- System Identification of FIR Filter Using Normalized LMS Algorithm
Identify an unknown system using normalized LMS algorithm.
- Compare Convergence Performance Between LMS Algorithm and Normalized LMS Algorithm
Compare the speed with which the adaptive filter algorithms converge.
- Signal Enhancement Using LMS and NLMS Algorithms
Introduces adaptive filters through a signal enhancement application.
- Noise Cancellation Using Sign-Data LMS Algorithm
Perform noise cancellation using sign-data LMS algorithm.
- System Identification Using RLS Adaptive Filtering
This example shows how to use a recursive least-squares (RLS) filter to identify an unknown system modeled with a lowpass FIR filter.
- Inverse System Identification Using RLS Algorithm
Perform inverse system identification using dsp.RLSFilter.
- Compare RLS and LMS Adaptive Filter Algorithms
Comparison of RLS and LMS adaptive filter algorithms.
- Adapt Multiple Filters Using LMS Update Block
Adapt multiple filters independently using the same LMS Update block. Use the Adapt port of the LMS Update block to selectively enable or disable the filters from being adapted.
- Model Adaptive Linear Combiner using LMS Update Block
Use LMS Update block as an adaptive linear combiner.
- Niederfrequentes Rauschen in Simulink mit einem adaptiven „Normalized LMS“-Filter entfernen
Entwerfen Sie einen adaptiven „Normalized LMS“-Filter und verwenden Sie ihn, um niederfrequentes Rauschen in Simulink® zu entfernen.
- Noise Cancellation in Simulink Using Normalized LMS Adaptive Filter
Remove colored noise generated from an acoustic environment, using a normalized LMS adaptive filter.
- Variable-Size Signal Support DSP System Objects
List of System objects that support variable-sized signals in DSP System Toolbox.
Verwandte Informationen
Enthaltene Beispiele
Adaptive Line Enhancer (ALE)
Apply adaptive filters to signal separation using a structure called an adaptive line enhancer (ALE). In adaptive line enhancement, a measured signal x(n) contains two signals, an unknown signal of interest v(n), and a nearly-periodic noise signal eta(n).
Adaptive Noise Cancellation Using RLS Adaptive Filtering
Use an RLS filter to extract useful information from a noisy signal. The information bearing signal is a sine wave that is corrupted by additive white Gaussian noise.
Acoustic Noise Cancellation (LMS)
Use the least mean square (LMS) algorithm to subtract noise from an input signal. The example uses a preconfigured Simulink® model. The LMS Filter block in the dspanc model models an adaptive filter that uses the reference signal at its Input port and the desired signal at the Desired port to automatically match the filter response. The LMS Filter block subtracts the filtered noise from the original signal. As the filter converges, the resultant error signal contains only the original signal.
Active Noise Control with Simulink Real-Time
Design a real-time active noise control system using a Speedgoat® Simulink® Real-Time™ target.
Adaptive Filter Convergence
Compares the rate of convergence for adaptive filters using different LMS algorithms.
Noise Canceler (RLS)
Subtract noise from an input signal using the Recursive Least Squares (RLS) algorithm. The RLS adaptive filter uses the reference signal on the Input port and the desired signal on the Desired port to automatically match the filter response in the Noise Filter block. As it converges to the correct filter, the filtered noise should be completely subtracted from the "Signal+Noise" signal, and the "Error Signal" should contain only the original signal.
Time-Delay Channel Estimation Through Adaptive Filtering
Adaptively estimate the time delay for a noisy input signal using the LMS adaptive FIR algorithm.
