Niederfrequentes Rauschen in Simulink mit einem adaptiven „Normalized LMS"-Filter entfernen - MATLAB & Simulink

Die Übersetzung dieser Seite ist veraltet. Klicken Sie hier, um die neueste Version auf Englisch zu sehen.

Niederfrequentes Rauschen in Simulink mit einem adaptiven „Normalized LMS“-Filter entfernen

Adaptive Filter verfolgen das dynamische Verhalten eines Systems und ermöglichen Ihnen, zeitvariable Signale zu beseitigen. Die Bibliotheken der DSP System Toolbox™ enthalten Blöcke, mit denen die Algorithmen Least-Mean-Square (LMS), Block-LMS, Fast-Block-LMS und Recursive-Least-Squares (RLS) für adaptive Filter implementiert werden können. Diese Filter minimieren die Differenz zwischen dem Ausgangssignal und dem gewünschten Signal, indem deren Filterkoeffizienten verändert werden. Das Ausgangssignal des adaptiven Filters nähert sich mit der Zeit immer mehr an das Signal, das Sie reproduzieren möchten, an.

Einen adaptiven Filter in Simulink entwerfen

In diesem Beispiel verwendet:

Live Script öffnen

In diesem Beispiel entwerfen Sie einen adaptiven LMS-Filter, um das niederfrequente Rauschen in Ihrem Signal zu entfernen:

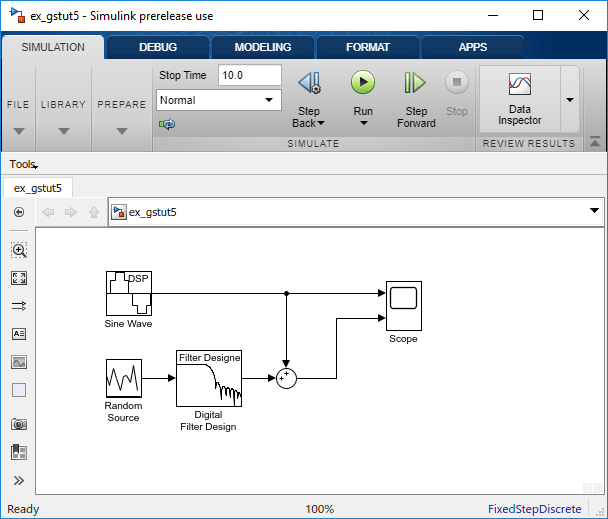
Wenn das Modell, das Sie in Einen digitalen Filter zu Ihrem Modell hinzufügen erstellt haben, auf Ihrem Desktop nicht geöffnet ist, öffnen Sie ex_gstut5, bei dem es sich um ein äquivalentes Modell handelt.

Öffnen Sie die Bibliothek der DSP System Toolbox™, indem Sie dsplib an der MATLAB®-Eingabeaufforderung eingeben.

Entfernen Sie das niederfrequente Rauschen in Ihrem Signal, indem Sie Ihrem System einen LMS Filter-Block hinzufügen. Im Szenario mit dem Flugzeug entspricht dies dem Subtrahieren des Windrauschens im Inneren des Cockpits vom Eingangssignal des Mikrofons. Doppelklicken Sie auf die Bibliothek „Filtering“ und dann auf die Bibliothek „Adaptive Filters“. Fügen Sie Ihrem Modell den Block „LMS Filter“ hinzu.

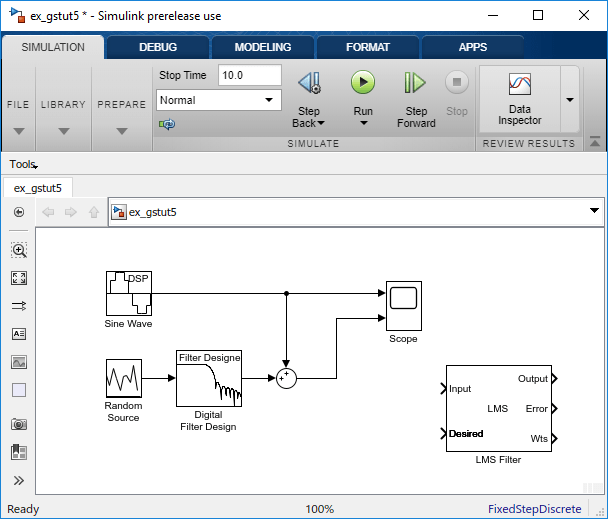
Legen Sie die Parameter für den Block „LMS Filter“ fest, um die Ausgabe des Blocks „Digital Filter Design“ zu modellieren. Öffnen Sie das Dialogfeld „LMS Filter“, indem Sie auf den Block doppelklicken. Legen Sie die Blockparameter wie folgt fest:

Algorithm = Normalized LMS
Filter length = 32
Specify step size via = Dialog
Step size (mu) = 0.1
Leakage factor (0 to 1) = 1.0
Initial value of filter weights = 0
Deaktivieren Sie das Kontrollkästchen Adapt port (Port anpassen).
Reset port = None
Aktivieren Sie das Kontrollkästchen Output filter weights (Filtergewichtungen ausgeben).

Basierend auf diesen Parametern berechnet der Block „LMS Filter“ die Filtergewichtungen mithilfe der normalisierten LMS-Gleichungen. Die Filterreihenfolge ist mit der des Blocks „Digital Filter Design“ identisch. Der Parameter Step size (mu) (Schrittgröße (mu)) definiert die Granularität der Filteraktualisierungsschritte. Da Sie den Parameter Leakage factor (0 to 1) (Leckfaktor (0 bis 1) auf „1.0“ festgelegt haben, hängen die aktuellen Werte der Filterkoeffizienten von den Anfangsbedingungen des Filters und von allen vorherigen Eingabewerten ab. Der Anfangswert der Filtergewichtungen (Koeffizienten) ist Null. Da Sie das Kontrollkästchen Output filter weights aktiviert haben, wird der Port Wts im Block angezeigt. An diesem Port gibt der Block die Filtergewichtungen aus.

Nachdem Sie die Blockparameter des Blocks „LMS Filter“ festgelegt haben, können Sie diesen Block in Ihr Blockdiagramm integrieren.

Einen adaptiven Filter zu Ihrem Modell hinzufügen

In diesem Beispiel verwendet:

Live Script öffnen

In diesem Beispiel stellen Sie Ihr ursprüngliches sinusförmiges Signal wieder her, indem Sie Ihrem System den adaptiven Filter hinzufügen, den Sie in Einen adaptiven Filter in Simulink entwerfen entworfen haben. Im Szenario mit dem Flugzeug modelliert der adaptive Filter das niederfrequente Rauschen, das im Inneren des Cockpits zu hören ist. Dadurch können Sie das Rauschen entfernen, sodass die Stimme des Piloten das einzige Eingangssignal des Mikrofons ist:

Wenn das Modell, das Sie in Einen adaptiven Filter in Simulink entwerfen erstellt haben, auf Ihrem Desktop nicht geöffnet ist, öffnen Sie ex_gstut6, bei dem es sich um ein äquivalentes Modell handelt.

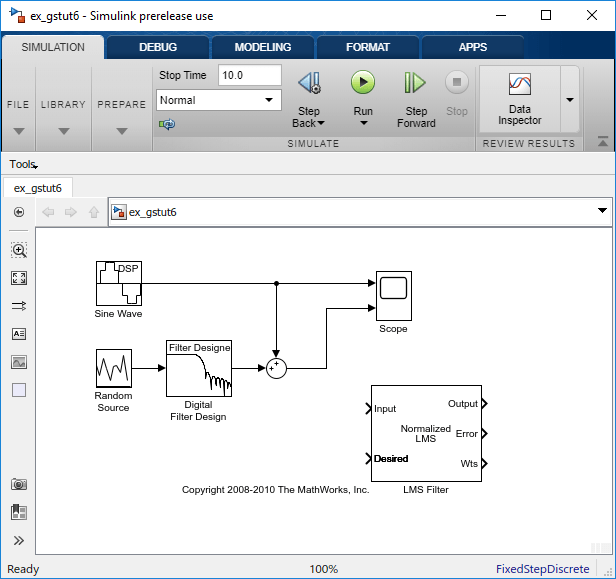
Fügen Sie in Ihrem Modell einen Summenblock hinzu, um das Ausgangssignal des adaptiven Filters vom sinusförmigen Signal mit niederfrequentem Rauschen zu subtrahieren. Ziehen Sie aus der Simulink™-Bibliothek „Math Operations“ einen Summenblock in Ihr Modell. Öffnen Sie das Dialogfeld „Sum“, indem Sie auf diesen Block doppelklicken. Legen Sie den Parameter List of signs auf |+- fest und klicken Sie dann auf OK.

Integrieren Sie den Block „LMS Filter“ in Ihr System.

Verbinden Sie den Ausgang des Blocks „Random Source“ mit dem Eingabeport des Blocks „LMS Filter“. Im Szenario mit dem Flugzeug ist das Zufallsrauschen das weiße Rauschen, das durch den Sensor an der Außenseite des Flugzeugs gemessen wird. Der Block „LMS Filter“ modelliert den Effekt des Flugzeugrumpfes auf das Rauschen.
Verbinden Sie den Ausgang des Blocks „Digital Filter Design“ mit dem Port „Desired“ am Block „LMS Filter“. Dies ist das Signal, das der LMS-Block reproduzieren soll.
Verbinden Sie den Ausgang des Blocks „LMS Filter“ mit dem negativen Port des Summenblocks, den Sie in Schritt 2 hinzugefügt haben.
Verbinden Sie den Ausgang des ersten Summenblocks mit dem positiven Port des zweiten Summenblocks. Ihr Modell sollte nun wie in der folgenden Abbildung aussehen.

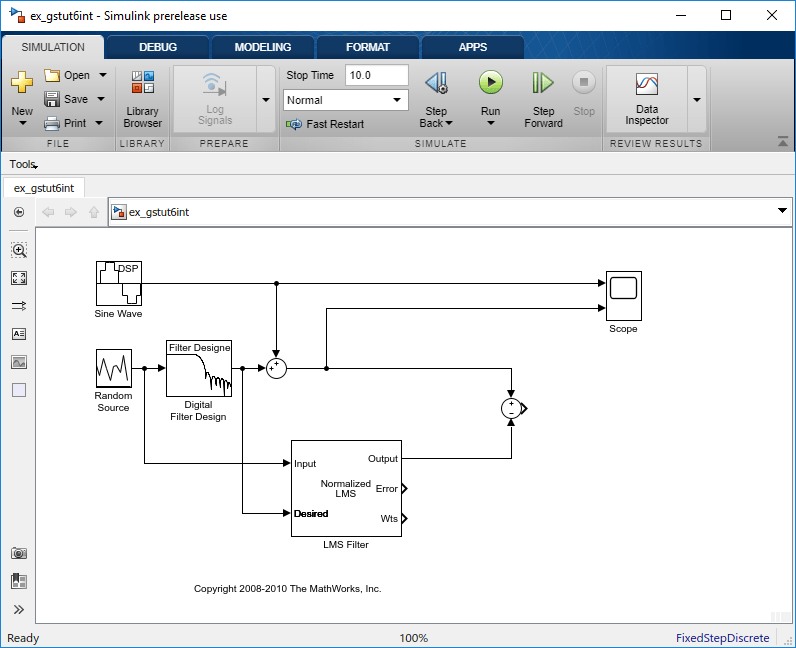
Der positive Eingang des zweiten Summenblocks ist die Summe aus dem Eingangssignal und dem niederfrequenten Rauschen, s(n) + y. Der negative Eingang des zweiten Summenblocks ist die beste Schätzung des Blocks „LMS Filter“ für das niederfrequente Rauschen, y'. Wenn Sie diese zwei Signale subtrahieren, haben Sie eine Näherung des Eingangssignals.

${s (n)}_{approx} = s (n) + y - y^{'}$

In dieser Gleichung gilt:

$s (n)$ ist das Eingangssignal.
${s (n)}_{approx}$ ist die Approximation des Eingangssignals.
$y$ ist das Rauschen, das durch den Block „Random Source“ und den Block „Digital Filter Design“ erzeugt wird.
$y^{'}$ ist die Approximation des Blocks „LMS Filter“ für das Rauschen.

Da der Block „LMS Filter“ nur eine Näherung des Rauschens modellieren kann, gibt es noch eine Differenz zwischen dem Eingangssignal und der Approximation des Eingangssignals. Richten Sie in den nachfolgenden Schritten den Block „Scope“ so ein, dass Sie das ursprüngliche sinusförmige Signal mit seiner Approximation vergleichen können.

Fügen Sie dem Block „Scope“ zwei zusätzliche Eingänge und Achsen hinzu. Öffnen Sie das Dialogfeld „Scope“, indem Sie auf den Block „Scope“ doppelklicken. Klicken Sie auf die Schaltfläche Parameters. Geben Sie für den Parameter Number of axes den Wert „4“ ein. Schließen Sie das Dialogfeld, indem Sie auf OK klicken.

Beschriften Sie die neuen Scope-Achsen. Klicken Sie im Fenster „Scope“ mit der rechten Maustaste auf die dritte Achse und wählen Sie Axes properties aus. Das Dialogfeld „Scope properties: axis 3“ wird geöffnet. Geben Sie in das Feld Title den Text Approximation of Input Signal ein. Schließen Sie das Dialogfeld, indem Sie auf OK klicken. Wiederholen Sie diese Prozedur für die vierte Achse und beschriften Sie sie mit Error.

Verbinden Sie den Ausgang des zweiten Summenblocks mit dem dritten Port des Blocks „Scope“.

Verbinden Sie den Ausgang des Ports Error am Block „LMS Filter“ mit dem vierten Port des Blocks „Scope“. Ihr Modell sollte nun wie in der folgenden Abbildung aussehen.

In diesem Beispiel ist das Ausgangssignal des Ports Error die Differenz zwischen dem gewünschten Signal des LMS-Filters und seinem Ausgangssignal. Da der Fehler niemals Null ist, modifiziert der Filter kontinuierlich die Filterkoeffizienten, um eine bessere Näherung des niederfrequenten Rauschens zu erreichen. Je besser die Näherung ist, desto mehr niederfrequentes Rauschen kann aus dem sinusförmigen Signal entfernt werden. Im nächsten Abschnitt, Die Koeffizienten Ihres adaptiven Filters anzeigen, erfahren Sie, wie Sie die Koeffizienten Ihres adaptiven Filters anzeigen können, da sie sich mit der Zeit ändern.

Die Koeffizienten Ihres adaptiven Filters anzeigen

In diesem Beispiel verwendet:

Live Script öffnen

Mit der Zeit ändern sich die Koeffizienten eines adaptiven Filters entsprechend einem ausgewählten Algorithmus. Sobald der Algorithmus die Leistung des Filters optimiert hat, erreichen diese Filterkoeffizienten ihren stabilen Zustand mit konstanten Werten. Während die Simulation ausgeführt wird, können Sie die Abweichung Ihrer Koeffizienten anzeigen, um festzustellen, ob sie ihren stabilen Zustand mit konstanten Werten erreicht haben. Danach können Sie bestimmen, ob Sie diese Werte in Ihrem tatsächlichen System implementieren können:

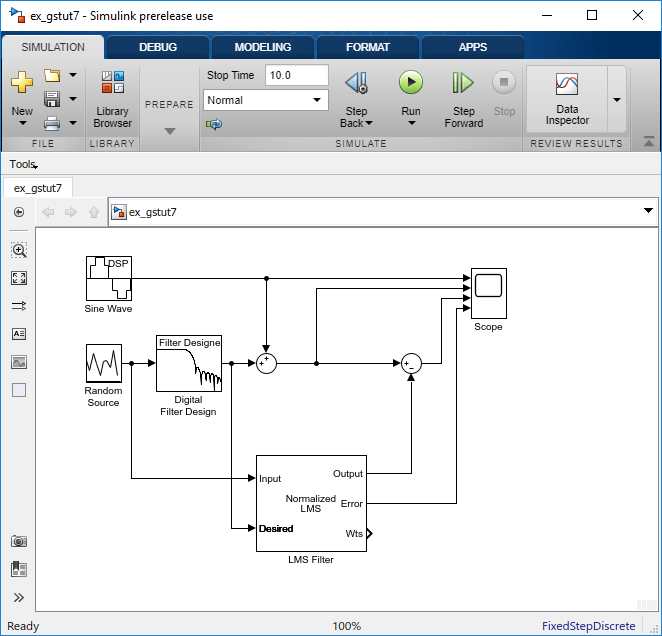
Wenn das Modell, das Sie in Einen adaptiven Filter zu Ihrem Modell hinzufügen erstellt haben, auf Ihrem Desktop nicht geöffnet ist, öffnen Sie ex_gstut7, bei dem es sich um ein äquivalentes Modell handelt.

Beachten Sie, dass der Port Wts des adaptiven Filters, an dem die Filtergewichtungen ausgegeben werden, noch verbunden werden muss.

Öffnen Sie die Bibliothek der DSP System Toolbox™, indem Sie dsplib an der MATLAB®-Eingabeaufforderung eingeben.

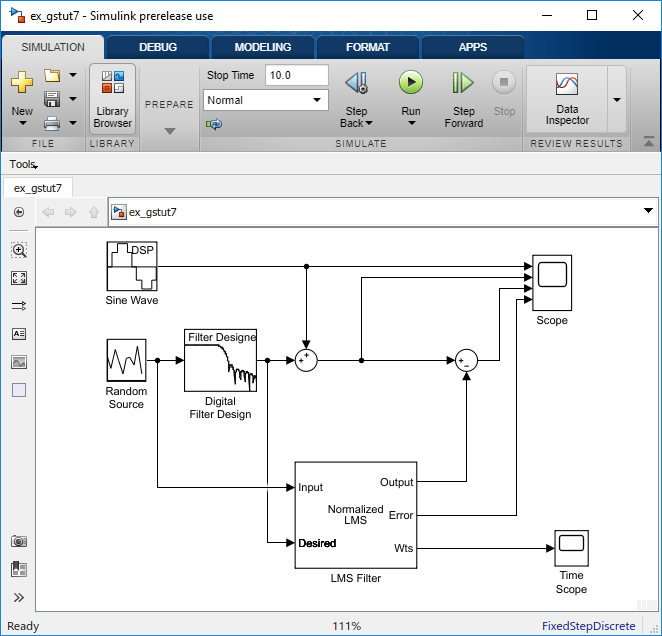
Zeigen Sie die Filterkoeffizienten an, indem Sie einen Time Scope-Block mit dem Port Wts des Blocks „LMS Filter“ verbinden.

Ändern Sie im Block „Time Scope“ die folgenden Konfigurationseigenschaften:

Time span = 0.05
Y-limits (Minimum) = -0.15
Y-limits (Maximum) = 0.5

Öffnen Sie die Modelleinstellungen. Klicken Sie dazu auf der Registerkarte Modeling auf Model Settings. Legen Sie im Fensterbereich Solver die folgenden Konfigurationsparameter fest:

Stop time = inf
Type = Fixed-step
Solver = discrete (no continuous states)

Diese Konfigurationsparameter empfehlen wir für Modelle, die „DSP System Toolbox“-Blöcke enthalten. Da diese Blöcke die Werte direkt berechnen, anstatt Differenzialgleichungen zu lösen, müssen Sie den Simulink®-Solver so konfigurieren, dass er sich wie ein Scheduler verhält. Im Scheduler-Modus verwendet der Solver die Abtastzeit eines Blocks, um zu bestimmen, wann der Code hinter dem Block ausgeführt wird. Für die Blöcke „Sine Wave“ und „Random Source“ in diesem Modell gilt zum Beispiel eine Abtastzeit von 0,05 Sekunden. Der Solver führt den Code hinter diesen Blöcken und hinter jedem weiteren Block mit dieser Abtastzeit aus, also einmal alle 0,05 Sekunden.

Hinweis: Bei der Arbeit mit Modellen, die „DSP System Toolbox“-Blöcke enthalten, sollten Sie Quell-Blöcke verwenden, die Ihnen die Angabe ihrer Abtastzeit ermöglichen. Wenn Ihr Quell-Block den Parameter Sample time nicht besitzt, müssen Sie Ihrem Modell einen „Zero-Order Hold“-Block hinzufügen und diesen Block zur Angabe der Abtastzeit verwenden. Weitere Informationen finden Sie unter Continuous-Time Source Blocks. Die Ausnahme von dieser Regel ist der „Constant“-Block, der eine konstante Abtastzeit besitzen kann. Wenn dies der Fall ist, führt Simulink diesen Block aus und zeichnet den konstanten Wert beim Start der Simulation einmal auf und danach immer dann, wenn Sie einen Parameter ändern. Dies ermöglicht schnellere Simulationen und einen kompakter generierten Code.

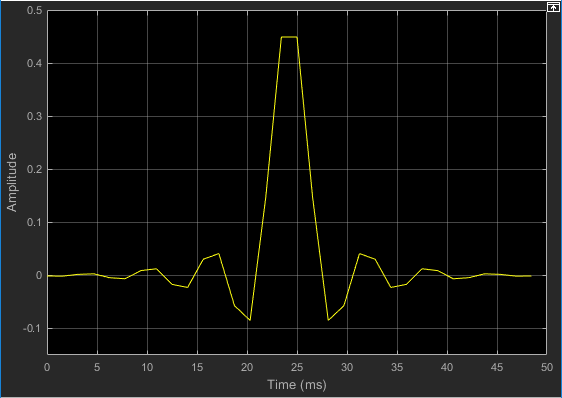
Führen Sie Ihr Modell aus und zeigen Sie das Verhalten Ihrer Filterkoeffizienten in der Komponente „Time Scope“ an, die beim Starten Ihrer Simulation automatisch geöffnet wird. Die Filterkoeffizienten nähern sich mit der Zeit ihrem stabilen Zustand mit konstanten Werten.

Das Verhalten des Systems können Sie auch im Fenster „Scope“ anzeigen. Sie können sehen, wie mit der Zeit der Fehler abnimmt und die Näherung des Eingangssignals immer mehr mit dem ursprünglichen sinusförmigen Signal übereinstimmt.

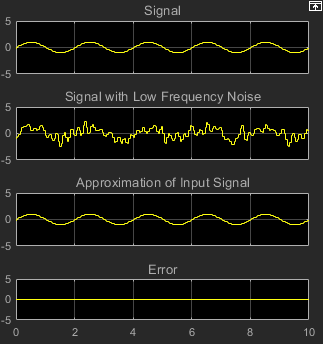
Jetzt haben Sie ein Modell erstellt, das in der Lage ist, das Rauschen adaptiv zu entfernen.

Zusammenfassung

Sie haben erfahren, wie Sie mithilfe des Blocks Digital Filter Design einen Tiefpassfilter entwerfen. Sie haben auch erfahren, wie Sie mithilfe des Blocks LMS Filter einen adaptiven Filter erstellen. Das Produkt DSP System Toolbox enthält weitere Blöcke, mit denen digitale und adaptive Filter entworfen und implementiert werden können. Weitere Informationen zu den Möglichkeiten der Filterung, die dieses Produkt bietet, finden Sie unter Filter Design und Filter Analysis.

Da die Abtastzeit aller Blöcke in diesem Modell identisch ist, ist dies ein Einfrequenz-Modell, das durch Simulink^® im Solver-Modus SingleTasking ausgeführt wird. Wenn sich die Abtastzeiten der Blöcke in Ihrem Modell unterscheiden, ist dies ein Mehrfrequenz-Modell, das durch Simulink im Solver-Modus MultiTasking ausgeführt werden kann. Weitere Informationen zu den Solver-Modi finden Sie unter Recommended Settings for Discrete-Time Simulations.

Wie sie Code aus Ihrem Modell mithilfe des Produkts Simulink Coder™ generieren, erfahren Sie unter Generate C Code from Simulink Model.

Siehe auch

LMS Filter | Digital Filter Design