freqsep
Slow-fast decomposition
Syntax
Description
[
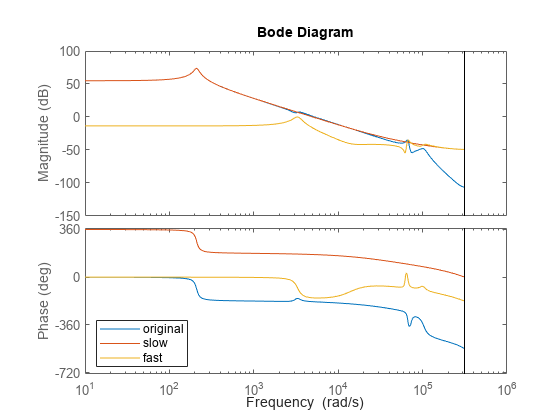
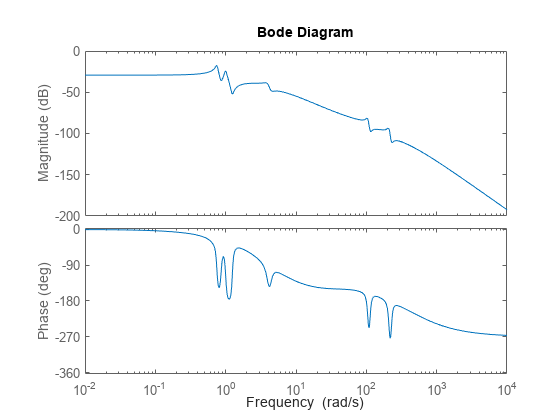
computes the decomposition where G1,G2]
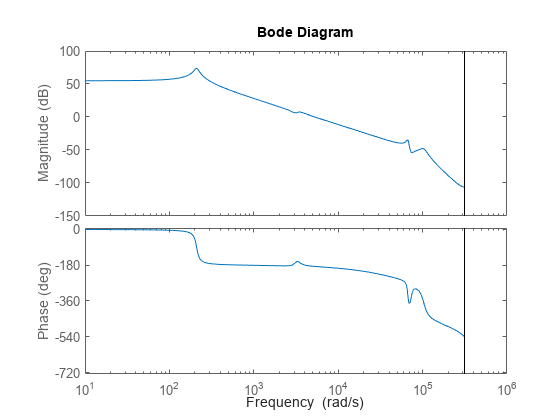
= freqsep(G,[fmin,fmax])G1 contains all modes with
natural frequency fmin ≤
ωn ≤
fmax and G2 contains the remaining modes. (since R2023b)