Train PyTorch Channel Prediction Models

Since R2025a

This example shows how to train a PyTorch™ based channel prediction neural network using data that you generate in MATLAB.

While this example demonstrates the use of PyTorch for training a channel prediction neural network, the Deep Learning Toolbox provides robust tools for implementing similar models directly within MATLAB.

Introduction

Wireless channel prediction is a crucial aspect of modern communication systems, enabling more efficient and reliable data transmission. Recent advancements in machine learning, particularly neural networks, have introduced a data-driven approach to wireless channel prediction. This approach does not rely on predefined models but instead learns directly from historical channel data. As a result, neural networks can adapt to realistic data, making them less sensitive to disturbances and interference.

Channel prediction using neural networks is fundamentally a time series learning problem since it involves forecasting future channel states based on past estimations. This method is particularly advantageous in environments where spatial correlation is minimal or absent, such as crowded urban areas with numerous moving objects. By focusing on temporal correlations and historical data, neural networks provide a computationally efficient and scalable solution across various environments.

Recurrent neural networks, such as long short-term memory (LSTM) and gated recurrent unit (GRU) networks, are strong candidates to predict channel response at a future time [1],[2]. These networks are suitable choices for time series prediction due to their ability to learn from historical data. LSTMs and GRUs are particularly effective for capturing temporal dependencies, with GRUs being more computationally efficient.

In this example, you train a GRU network defined in PyTorch. The nr_channel_predictor.py file contains the neural network definition, training and other functionality for the PyTorch network. The nr_channel_predictor_wrapper.py file contains the interface functions that minimize data transfer between MATLAB and Python processes. The PyTorch Wrapper Template section shows how to create the interface functions using a template.

You generate data in MATLAB as described in the Prepare Data for CSI Processing example. You train the network in PyTorch using the Python interface in MATLAB.

Set Up Python Environment

Before running this example, set up the Python environment as explained in PyTorch Coexecution. Specify the full path of the Python executable to use in the pythonPath field below. The helperSetupPyenv function sets the Python environment in MATLAB according to the selected options and checks that the libraries listed in the requirements_chanest.txt file are installed. This example is tested with Python version 3.10.4.

if ispc
  pythonPath = ".\.venv\Scripts\pythonw.exe";
else
  pythonPath = "./venv_linux/bin/python3";
end
requirementsFile = "requirements_chanpre.txt";
executionMode = "OutOfProcess";
currentPyenv = helperSetupPyenv(pythonPath,executionMode,requirementsFile);

Setting up Python environment
Parsing requirements_chanpre.txt 
Checking required package 'numpy'
Checking required package 'torch'
Required Python libraries are installed.

You can use the following process ID and name to attach a debugger to the Python interface and debug the example code.

fprintf("Process ID for '%s' is %s.\n", ...
  currentPyenv.ProcessName,currentPyenv.ProcessID)

Process ID for 'MATLABPyHost' is 5584.

Preload the Python module for faster start.

module = py.importlib.import_module('nr_channel_predictor_wrapper');

Prepare Data

The GRU network requires the input data to be a 3-D array. The features are channel estimates from transmit antennas, where the real and imaginary parts are interleaved per sample. The sequence is the present and $$N_{seq}-1$$ previous symbols, where $$N_{seq}$$ is the sequence length. The sequence symbols are sampled at every $$T_s$$ seconds. Each feature sequence is a 2-D time sample. A time sample is calculated for each symbol in all subcarriers, receive antennas, and frames. As a result, the network considers only one subcarrier and receive antenna at a time in the input and output of the prediction. For ease of presentation, the following figure shows features as rows, sequences as columns, and time samples as pages. The GRU network requires the time samples to be the first dimension, followed by the sequence dimension and the features dimension.

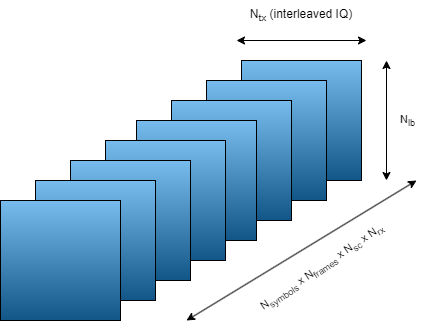
The target data is a 2-D array, where the first dimension is the time samples that correspond to the time samples of the input data and the second dimension is the transmit antenna samples at a given horizon (future time step).

Generate Channel Estimates

Generate training and validation data. The helperChanPreGenerateData function generates perfect channel estimates and saves them into one data file per frame. For details, see the Prepare Data for CSI Processing example. The data generation takes about 15 seconds on an Intel® Xeon® W-2133 CPU with six cores @ 3.60 GHz.

txAntennaSize = 2;
rxAntennaSize = 2;
rmsDelaySpread = 300e-9;     % s
maxDoppler = 37;            % Hz
nSizeGrid = 52;              % Number resource blocks (RB)
subcarrierSpacing = 15;      % 15, 30, 60, 120 kHz
numerology = (subcarrierSpacing/15)-1;

channel = nrTDLChannel;
channel.DelayProfile = 'TDL-A';
channel.DelaySpread = rmsDelaySpread;       % s
channel.MaximumDopplerShift = maxDoppler;   % Hz
channel.RandomStream = "Global stream";
channel.NumTransmitAntennas = txAntennaSize;
channel.NumReceiveAntennas = rxAntennaSize;
channel.ChannelFiltering = false;

% Carrier definition
carrier = nrCarrierConfig;
carrier.NSizeGrid = nSizeGrid;
carrier.SubcarrierSpacing = subcarrierSpacing;

numSamples = 10e6;
numSlotsPerFrame = 100;     % reset channel after each 100 slots

helperChanPreGenerateData(numSamples,numSlotsPerFrame,channel,carrier);

Data exists. Skipping generation.

Load Saved Data

The data is saved in multiple files. Each file contains one frame of data with dimensions [$$N_{sc}$$ -by- $$N_{symbol}$$ -by- $$N_{rx}$$ -by- $$N_{tx}$$]. Use the signalDatastore function to load the data into memory.

channelDataFilePrefix = "nr_channel_est";
baseFolder = ".";
sds = signalDatastore(fullfile(baseFolder,"Data",channelDataFilePrefix+"_*"));
HestCell = readall(sds);

The signalDatastore reads each file into a cell. Concatenate the data into an array with dimensions [$$N_{sc}$$ -by- $$N_{symbol}$$ -by- $$N_{rx}$$ -by- $$N_{tx}$$ -by- $$N_{frame}$$].

dimSubcarrier = 1;
dimSymbol = 2;
dimRxAntenna = 3;
dimTxAntenna = 4;
dimFrame = 5;
dimIQ = 6;
Hest = cat(dimFrame,HestCell{:});
clear HestCell

Since the data is complex and the network requires real-valued data, separate the real and imaginary parts and store them on the sixth dimension.

HestReal = cat(dimIQ,real(Hest),imag(Hest));

Get the dimensions of the data.

[Nsc,Nsymbol,Nrx,Ntx,Nframe,Niq] = size(HestReal,[dimSubcarrier,dimSymbol,dimRxAntenna,dimTxAntenna,dimFrame,dimIQ])

Nsc = 
624

Nsymbol = 
1400

Nrx = 
2

Ntx = 
2

Nframe = 
6

Niq = 
2

Reshape Data

Create an array with transmitter antenna samples with interleaved IQ samples as the first dimension and symbols on the second dimension.

In HestReal, the symbols are time-contiguous only in the symbol dimension, which is the second dimension. Switching subcarriers, receive antennas, and frames creates discontinuities in the symbol dimension. To ensure continuity in the symbol dimension, keep the second dimension separate but combine subcarriers, receive antennas, and frames as the third dimension.

To create this array, first permute the dimensions to obtain an [$$N_{iq}$$-by-$$N_{tx}$$-by-$$N_{sym}$$-by-$$N_{sc}$$-by-$$N_{rx}$$-by-$$N_{frame}$$] array. This case has only one frame in this case.

H = permute(HestReal,[dimIQ dimTxAntenna dimSymbol dimSubcarrier dimRxAntenna dimFrame]);
disp(size(H))

           2           2        1400         624           2           6

Reshape the array to size [$$N_{tx}{N}_{iq}$$-by-$$N_{symbol}$$-by-$$N_{other}$$], where $$N_{other}$$ is $$N_{sc}{N}_{frame}{N}_{rx}$$. Since MATLAB reads arrays starting from the first dimension, this operation creates an array where the first dimension contains the interleaved IQ samples for the transmit antennas, the second dimension is time-contiguous symbols, and the third dimension is subcarriers, receive antennas, and frames.

Hr = reshape(H,Ntx*Niq,Nsymbol,Nsc*Nrx*Nframe);
[Ntxiq,Nsymbol,Nother] = size(Hr)

Ntxiq = 
4

Nsymbol = 
1400

Nother = 
7488

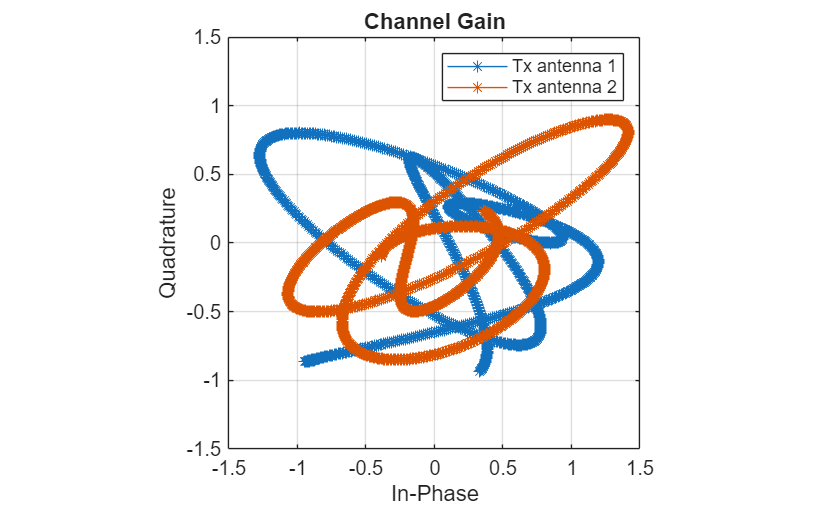
Plot the variation of the channel gain for the two transmit antennas for a random subcarrier, receive antenna, and frame.

figure
Hsample = Hr(:,:,randi(Nsc*Nrx*Nframe));
plot(Hsample(1:2:end,:)',Hsample(2:2:end,:)', '*-')
lim = floor(max(abs(Hsample),[],"all")*11)/10;
ylim([-lim lim])
xlim([-lim lim])
axis square
grid on
xlabel("In-Phase")
ylabel("Quadrature")
legend("Tx antenna 1","Tx antenna 2")
title("Channel Gain")

Add Noise

To simulate noisy channel estimates, add noise to the channel data. Set the value for signal-to-noise ratio (SNR).

SNR = 20;

Calculate the noise variance that you need to simulate the required SNR value.

$$\begin{array}{l}SNR=10lo{g}_{10}(S/N)\\ \frac{S}{N}=10^{(SNR/10)}\\ N=\frac{S}{10^{(SNR/10)}}\end{array}$$

noiseVariance = (var(Hr,[],"all")/10^(SNR/10))/2;

Generate noisy data.

Hnoisy = Hr + randn(size(Hr),"single")*sqrt(noiseVariance);

Normalize Data

When working with Gated Recurrent Units (GRUs), input data normalization is crucial because it helps the network learn patterns more effectively, especially in time series data where values can vary significantly across different magnitudes, by ensuring all features are on a similar scale; this is particularly important for optimal training and performance of a GRU model. First, plot the histogram of the input data samples.

histogram2(Hnoisy(1:2:end,:,:),Hnoisy(2:2:end,:,:),40)
grid on
xlabel("In-phase Data Amplitude")
ylabel("Quadrature Data Amplitude")
zlabel("Number of Occurances")

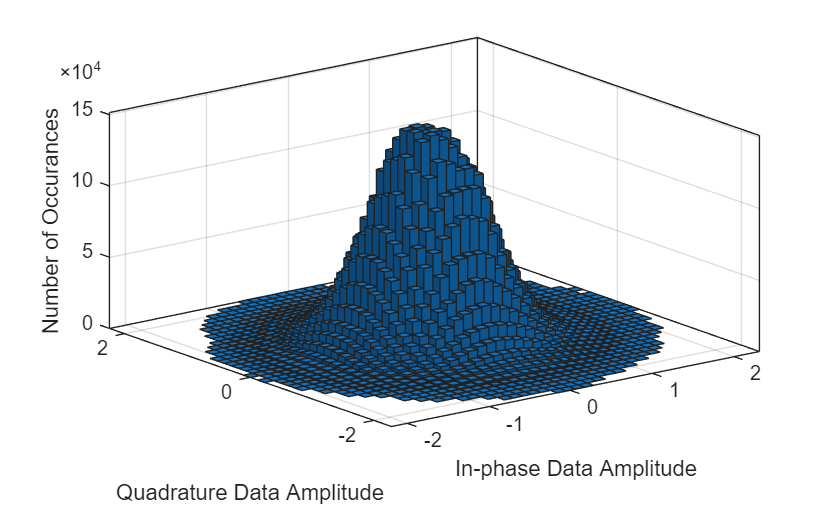
The histogram shows no outliers. Use min-max scaling to scale the data to a range between 0 and 1 by subtracting the minimum value and dividing by the range of the data. Check the minimum and maximum values of features.

featuresMax = max(Hnoisy,[],[2 3])

featuresMax = 4×1 single column vector

    2.0115
    1.9520
    2.3068
    2.2548

featuresMin = min(Hnoisy,[],[2 3])

featuresMin = 4×1 single column vector

   -2.1160
   -2.1696
   -2.1018
   -2.2361

Since all features are within a similar range, apply min-max scaling to the whole data.

dataMax = max(featuresMax);
dataMin = min(featuresMin);
Hnoisys = (Hnoisy - dataMin) / (dataMax - dataMin);
Hrs = (Hr - dataMin) / (dataMax - dataMin);

Format Input Data

The network requires an input where the first dimension is symbols in time. The second dimension is the previous time steps (symbols) that you used in prediction, and the third dimension is the transmit antenna symbols. Decide on the number of time steps on the second dimension based on the coherence time of the channel. The coherence time of the channel is approximately

$$T_c\approx \frac{1}{2\times \text{Doppler}\text{Spread}}$$, which is

Tc = 1/(2*maxDoppler)

Tc = 
0.0135

seconds. Calculate coherence time in slot time.

Tslot = 1e-3 / 2^numerology;
symbolsPerSlot = 14;
symbolTime = Tslot/symbolsPerSlot;
coherenceTimeInSlots = Tc / Tslot

coherenceTimeInSlots = 
13.5135

Use four times the coherence time as the length of the input sequence to predict channel gain in the future.

sequenceLength = ceil(coherenceTimeInSlots*4)

sequenceLength = 
55

This sequenceLength value provides enough variation in the channel for the network to learn channel characteristics.

plot(Hnoisys(:,1:sequenceLength*symbolsPerSlot,randi(size(Hnoisys,3)))')
grid on
xlabel("Symbols")
ylabel("Channel gain")
legend("Tx1-I","Tx1-Q","Tx2-I","Tx2-Q")

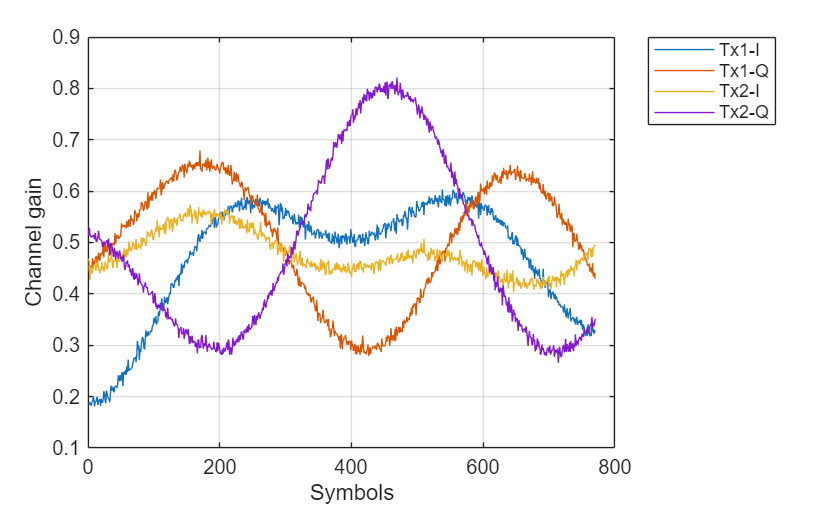
Sample $$N_{seq}$$ symbols from the second dimension of the Hnoisy array at $$N_{ts}$$ period from the second dimension, which contains the time-contiguous symbols. This 2-D array is the $$2N_{tx}$$-by-$$N_{seq}$$ input data sample. Repeat this process for each time step in the second dimension and for each subcarrier, receiver antenna, and frame (third dimension). Since each sample requires $$N_{seq}$$ previous symbols sampled at $$T_s$$, input data can have only $$N_{symbol}-N_{ts}(N_{seq}-1)$$ time-contiguous samples. First preallocate inputData as a $$N_{seq}$$-by-2$$N_{tx}$$-by-$$N_{symbol}-N_{ts}(N_{seq}-1)$$ single precision array.

inputData = zeros(Ntxiq,sequenceLength,floor((Nsymbol-(sequenceLength-1)*symbolsPerSlot)*Nsc*Nrx*Nframe),"single");

Sample the data using a for loop over time-contiguous symbols (s), and subcarriers, receive antennas, and frames (p). While switching subcarriers, receive antennas, and frames, channel samples experience discontinuities. The sequence samples must be continuous.

sample = 1;
for p = 1:Nsc*Nrx*Nframe
  for s = 1:1:(Nsymbol - (sequenceLength-1)*symbolsPerSlot)
    inputData(:,:,sample) = Hnoisys(:,s:symbolsPerSlot:(s+symbolsPerSlot*(sequenceLength-1)+1),p);
    sample = sample + 1;
  end
end

Permute the data to bring time to the first dimension as the PyTorch networks expect time to be the first dimension.

inputData = permute(inputData,[3,2,1]);

Check the size of the input data array.

size(inputData)

ans = 1×3

     4822272          55           4

Check the size of the input data array in the memory.

varInfo = whos("inputData");
fprintf("inputData is %1.0f MB in memory.\n", varInfo.bytes / 2^20)

inputData is 4047 MB in memory.

Format Target Data

Generate target data based on the prediction horizon. Select horizon, in milliseconds. Target data contains interleaved IQ samples for transmit antennas in the first dimension and symbols on the second dimension. The targetData variable holds the channel noisy estimation samples and used as target values during training.

horizon = 2; % ms
targetData = zeros(Ntxiq,(Nsymbol-(sequenceLength-1+horizon)*symbolsPerSlot)*Nsc*Nrx*Nframe,"single");
sample = 1;
for p = 1:Nsc*Nrx*Nframe
  targetData(:,sample:sample+(Nsymbol-(sequenceLength-1+horizon)*symbolsPerSlot)-1) = ...
    Hrs(:,((sequenceLength-1)+horizon)*symbolsPerSlot+1:end,p);
  sample = sample+(Nsymbol-(sequenceLength-1+horizon)*symbolsPerSlot);
end

Permute to bring time to the first dimension as the PyTorch networks expect time to be the first dimension.

targetData = permute(targetData,[2,1]);
size(targetData)

ans = 1×2

     4612608           4

Select Training and Validation Data

Define the number of training and validation samples.

numTraining = 90000;
numValidation = 10000;

Randomly sample the input and target data on the time dimension to select training and validation samples. Since each $$2N_{tx}$$-by-$$N_{lb}$$ sample is independent, this case has no time continuity requirement.

idxRand = randperm(size(targetData,1));

Select training and validation data.

xTraining = inputData(idxRand(1:numTraining),:,:);
xValidation = inputData(idxRand(1+numTraining:numValidation+numTraining),:,:);

yTraining = targetData(idxRand(1:numTraining),:);
yValidation = targetData(idxRand(1+numTraining:numValidation+numTraining),:);

Check the in-memory size of generated data.

varInfo = whos("xTraining","xValidation","yTraining","yValidation");
fprintf("xTraining is %1.1f MB in memory.\n", varInfo(1).bytes / 2^20)

xTraining is 75.5 MB in memory.

fprintf("xValidation is %1.1f MB in memory.\n", varInfo(2).bytes / 2^20)

xValidation is 8.4 MB in memory.

fprintf("yTraining is %1.1f MB in memory.\n", varInfo(3).bytes / 2^20)

yTraining is 1.4 MB in memory.

fprintf("yValidation is %1.0f kB in memory.\n", varInfo(4).bytes / 2^10)

yValidation is 156 kB in memory.

Initiate Neural Network

Initialize the channel predictor neural network. Set GRU hidden size to 64 and number of hidden GRU units to 2. The chanPredictor variable is the PyTorch model for the GRU based channel predictor.

gruHiddenSize = 128;
gruNumLayers  = 2;
chanPredictor = py.nr_channel_predictor_wrapper.construct_model(...
  Ntx, ...
  gruHiddenSize, ...
  gruNumLayers);

py.nr_channel_predictor_wrapper.info(chanPredictor)

Model architecture:
ChannelPredictorGRU(
  (gru): GRU(4, 128, num_layers=2, batch_first=True, dropout=0.5)
  (batch_norm): BatchNorm1d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (fc): Linear(in_features=128, out_features=4, bias=True)
)

Total number of parameters: 151300

Train Neural Network

The nr_channel_predictor_wrapper.py file contains the MATLAB interface functions to train the channel predictor neural network. Set values for hyperparameters number of epochs, batch size, initial learning rate, and validation frequency in epochs. Call the train function with required inputs to train and validate the chanPredictor model. Set the verbose variable to true to print out training progress. Training and testing for 2000 epochs takes about 90 minutes on a PC that has NVIDIA® TITAN V GPU with a compute capability of 7.0 and 12 GB memory. Set trainNow to true by clicking the check box to train the network. If your GPU runs out of memory during training, reduce the batch size.

trainNow = false;
if trainNow
  numEpochs            =2000;
  batchSize            = 128;
  initialLearningRate  = 5e-3;
  validationFrequency  = 5;
  verbose              = true;
  tStart = tic;
  result = py.nr_channel_predictor_wrapper.train( ...
    chanPredictor, ...
    xTraining, ...
    yTraining, ...
    xValidation, ...
    yValidation, ...
    initialLearningRate, ...
    batchSize, ...
    numEpochs, ...
    validationFrequency, ...
    verbose);
  et = toc(tStart); et = seconds(et); et.Format = "hh:mm:ss.SSS";

The output of the train Python function is a cell array with five elements. The output contains the following in order:

• Trained PyTorch model

• Training loss array (per iteration)

• Validation loss array (per epoch)

• Outdated error (with respect to current channel estimate)

• Time spent in Python

Parse the function output and display the results.

  chanPredictor = result{1};
  trainingLoss = single(result{2});
  validationLoss = single(result{3});
  finalValidationLoss = validationLoss(end);
  elapsedTimePy = result{4};
  etInPy = seconds(elapsedTimePy);
  etInPy.Format="hh:mm:ss.SSS";  

Save the network for future use together with the training information.

  modelFileName = sprintf("channel_predictor_gru_horizon%d_epochs%d",horizon,numEpochs);
  fileName = py.nr_channel_predictor_wrapper.save_model_weights( ...
    chanPredictor, ...
    modelFileName);
  infoFileName = modelFileName+"_info";
  save(infoFileName,"dataMax","dataMin","trainingLoss","validationLoss", ...
    "etInPy","et","initialLearningRate","batchSize","numEpochs","validationFrequency", ...
    "Ntx","gruHiddenSize","gruNumLayers");
  fprintf("Saved network in '%s' file and\nnetwork info in '%s.mat' file.\n", ...
    string(fileName),infoFileName)
else

When called with a filename as the last input, the construct_model function creates a neural network and loads the trained weights from the file. Run the network with xValidation input by calling the predict Python function.

  numEpochs = 2000;
  horizon = 2;
  modelFileName = sprintf("channel_predictor_gru_horizon%d_epochs%d.pth",horizon,numEpochs);
  infoFileName = sprintf("channel_predictor_gru_horizon%d_epochs%d_info.mat",horizon,numEpochs);
  chanPredictor = py.nr_channel_predictor_wrapper.construct_model( ...
    Ntx, ...
    gruHiddenSize, ...
    gruNumLayers, ...
    modelFileName);
  y = py.nr_channel_predictor_wrapper.predict( ...
    chanPredictor, ...
    xValidation);

Calculate the mean square error (MSE) loss as compared to the expected channel estimates.

  y = single(y);
  finalValidationLoss = mean(sum(abs(y - yValidation).^2,2)/Ntx);

Load the training and validation loss logged during training.

  load(infoFileName,"validationLoss","trainingLoss","etInPy","et")
end
fprintf("Validation Loss: %f dB",10*log10(finalValidationLoss))

Validation Loss: -13.515863 dB

The overhead caused by the Python interface is insignificant.

fprintf("Total training time: %s\nTraining time in Python: %s\nOverhead: %s\n",et,etInPy,et-etInPy)

Total training time: 03:09:00.219
Training time in Python: 03:08:45.142
Overhead: 00:00:15.077

Plot the training and validation loss. As the number of iterations increases, the loss value converges to about $$-20$$ dB.

figure
plot(10*log10(trainingLoss));
hold on
numIters = size(trainingLoss,2);
iterPerEpoch = numIters/length(validationLoss);
plot(iterPerEpoch:iterPerEpoch:numIters,10*log10(validationLoss),"*-");
hold off
legend("Training", "Validation")
xlabel(sprintf("Iteration (%d iterations per epoch)",iterPerEpoch))
ylabel("Loss (dB)")
title("Training Performance (NMSE as Loss)")
grid on

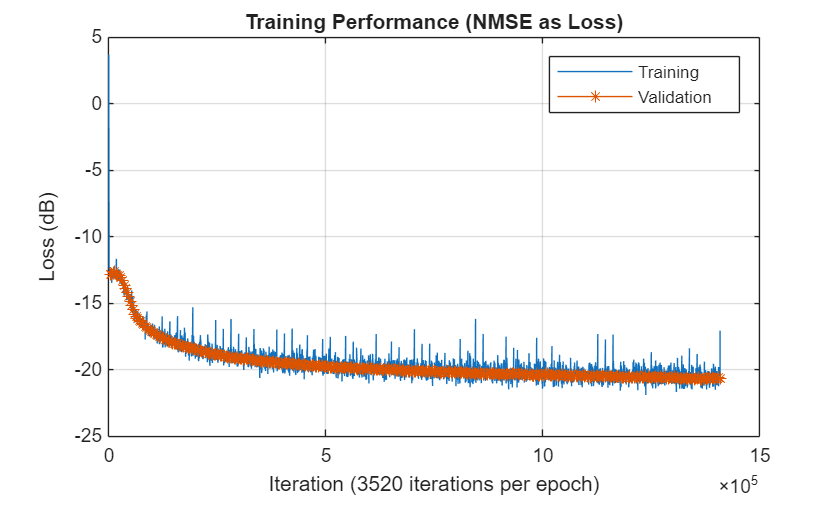
Investigate Network Performance

Test the network for different horizon values. The helperChanEstCompareNetworks function trains and tests the GRU channel prediction network for the horizon values specified in the horizonVec variable.

trainForComparisonNow = false;
if trainForComparisonNow
  horizonVec = [0:5 10];
  gruHiddenSize        = 64;
  gruNumLayers         = 2;
  numEpochs            = 2000;
  batchSize            = 128;
  initialLearningRate  = 5e-3;
  validationFrequency  = 5;
  compTable = helperChanPreCompareNetworks(Hrs,Hnoisys,sequenceLength, ...
    horizonVec,gruHiddenSize,gruNumLayers,numTraining,numValidation, ...
    numEpochs,batchSize,initialLearningRate,validationFrequency);
else
  load dChannelPredictionNetworkHorizonResults compTable horizonVec numEpochs numTraining numValidation
end

The plotValidationLoss function plots the simulated validation loss values for all three network architectures. As the prediction horizon increases, the validation loss, which is the average error for channel prediction, also increases.

plotValidationLoss(compTable,horizonVec);

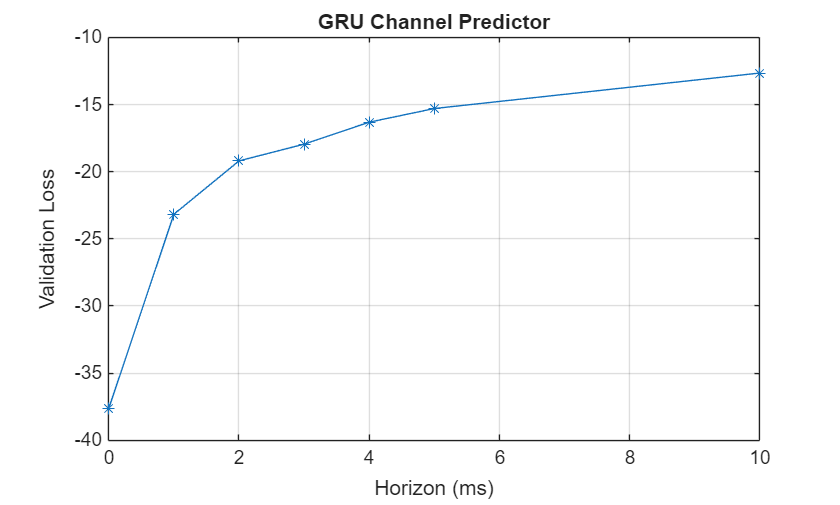
References

[1] W. Jiang and H. D. Schotten, "Recurrent Neural Network-Based Frequency-Domain Channel Prediction for Wideband Communications," 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 2019, pp. 1-6, doi: 10.1109/VTCSpring.2019.8746352.

[2] O. Stenhammar, G. Fodor and C. Fischione, "A Comparison of Neural Networks for Wireless Channel Prediction," in IEEE Wireless Communications, vol. 31, no. 3, pp. 235-241, June 2024, doi: 10.1109/MWC.006.2300140.

PyTorch Wrapper Template

You can use your own PyTorch models in MATLAB using the Python interface. The py_wrapper_template.py file provides a simple interface with a predefined API. This example uses the following API set:

• construct_model: returns the PyTorch neural network model

• train: trains the PyTorch model

• save_model_weights: saves the PyTorch model weights

• load_model_weights: loads the PyTorch model weights

• info: prints or returns information on the PyTorch model

The Online Training and Testing of PyTorch Model for CSI Feedback Compression example shows an online training workflow and uses the following API set in addition to the one used in this example.

• setup_trainer: sets up a trainer object for with online training

• train_one_iteration: trains the PyTorch model for one iteration for online training

• validate: validates the PyTorch model for online training

• predict: runs the PyTorch model with the provided input(s)

You can modify the py_wrapper_template.py file. Follow the instruction in the template file to implement the recommended entry points. Delete the entry points that are not relevant to your project. Use the entry point functions as shown in this example to use your own PyTorch models in MATLAB.

Local Function

function plotValidationLoss(compTable,horizonVec)
metric = "ValidationLoss";
val = compTable{compTable.Model=="GRU",metric};
plot(horizonVec,10*log10(val(:,end)),"-*")
grid on
xlabel("Horizon (ms)")
ylabel("Validation Loss")
title("GRU Channel Predictor")
end