M-PSK Modulator Baseband

Modulate using M-ary phase shift keying

• 

Libraries:
Communications Toolbox / Modulation / Digital Baseband Modulation / PSK
Communications Toolbox HDL Support / Modulation / PM

Description

The M-PSK Modulator Baseband block modulates an input signal using M-ary phase shift keying (PSK) and returns a complex baseband output. The modulation order, M, which is equivalent to the number of points in the signal constellation, is determined by the M-ary number parameter. The block accepts scalar or column vector input signals.

Examples

Modulate and Demodulate 8-PSK Signal

Generate and demodulate a noisy 8-PSK signal.

Open the doc_8psk_model model. The model generates random data using the Random Integer Generator block. To modulate the random data, the model uses the M-PSK Modulator Baseband block with a modulation order of 8 and a constellation order set to Gray. Subsequently, the modulated data passes through an additive white Gaussian noise channel (AWGN Channel block). The model displays the noisy constellation through the Constellation Diagram block. To demodulate this noisy signal, it employs the M-PSK Demodulator Baseband block with the same modulation and constellation order as the modulator. Finally, the model computes the error statistics using the Error Rate Calculation.

Run the model.

Collect the error statistics in a vector, ErrorVec. Observe that the number of symbol errors is zero when Eb/No is 15 dB.

Number of symbol errors = 0

Change the Eb/No of the AWGN Channel block from 15 dB to 5 dB. The constellation diagram shows the increase in the noise.

Because of the increase in the noise level, the number of symbol errors is greater than zero.

Number of symbol errors = 21

Gray-Coded M-PSK Modulation Error Rate in AWGN Channel Using Simulink

This example uses the doc_gray_code to compute bit error rates (BER) and symbol error rates (SER) for M-PSK modulation. The theoretical error rate performance of M-PSK modulation in AWGN is compared to the error rate performance for Gray-coded symbol mapping and to the error rate performance of binary-coded symbol mapping.

The Random Integer Generator block serves as the source, producing a sequence of integers. The Integer to Bit Converter block converts each integer into a corresponding binary representation. The M-PSK Modulator Baseband block in the doc_gray_code model:

• Accepts binary-valued inputs that represent integers in the range [0, (M - 1], where M is the modulation order.

• Maps binary representations to constellation points using a Gray-coded ordering.

• Produces unit-magnitude complex phasor outputs, with evenly spaced phases in the range [0, (2 (M - 1) / M)].

The AWGN Channel block adds white Gaussian noise to the modulated data. The M-PSK Demodulator Baseband block demodulates the noisy data. The Bit to Integer Converter block converts each binary representation to a corresponding integer. Then two separate Error Rate Calculation blocks calculate the error rates of the demodulated data. The block labeled SER Calculation compares the integer data to compute the symbol error rate statistics and the block labeled BER Calculation compares the bits data to compute the bit error rate statistics. The output of the Error Rate Calculation block is a three-element vector containing the calculated error rate, the number of errors observed, and the amount of data processed.

To reduce simulation run time and ensure that the statistics of the errors remain stable as the Eb/N0 ratio increases, the model is configured to run until 100 errors occur or until 1e8 bits have been transmitted.

The model initializes variables used to configure block parameters by using the PreLoadFcn callback function. For more information, see Model Callbacks (Simulink).

Produce Error Rate Curves

Compute the theoretical BER for nondifferential 8-PSK in AWGN over a range of Eb/N0 values by using the berawgn function. Simulate the doc_gray_code model with Gray-coded symbol mapping over the same range of Eb/N0 values.

Compare Gray coding with binary coding, by modifying the M-PSK Modulator Baseband and M-PSK Demodulator Baseband blocks to set the Constellation ordering parameter to Binary instead of Gray. Simulate the doc_gray_code model with binary-coded symbol mapping over the same range of Eb/N0 values.

Plot the results by using the semilogy function. The Gray-coded system achieves better error rate performance than the binary-coded system. Further, the Gray-coded error rate aligns with the theoretical error rate statistics.

Ports

Input

In_1 — Input signal

scalar | vector

Specify the input signal as an integer scalar, integer vector, or binary vector.

• When Input type is Integer, specify the input signal elements as integers from 0 to M – 1.

• When Input type is Bit, specify the input signal as a binary vector in which the number of elements is an integer multiple of the bits per symbol. The bits per symbol is equal to log₂(M).

Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean

Output

Out_1 — Output signal

scalar | vector

Output signal, returned as a complex scalar or vector. The output is the complex baseband representation of the PSK-modulated signal.

Data Types: single | double | fixed point

Parameters

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Main

M-ary number — Modulation order of the PSK constellation

8 (default) | scalar

Specify the modulation order as a positive integer power of two.

Example: 2 | 16

Input type — Type of input signal

Integer (default) | Bit

Specify the elements of the input signal as integers or bits. If Input type is Bit, the number of samples per frame must be an integer multiple of the number of bits per symbol. The number of bits per symbol is log₂(M).

Constellation ordering — Symbol mapping

Gray (default) | Binary | User-defined

Symbol mapping of integer or groups of log₂(M) bit inputs, specified as Gray, Binary, or User-defined.

• When you set Constellation ordering to Gray, the input signal is mapped to the output symbols using a Gray-encoded signal constellation.

• When you set Constellation ordering to Binary, the modulated symbol is exp(jϕ+j2πm/M), where ϕ is the phase offset in radians, m is the integer input such that 0 ≤ m ≤ M – 1, and M is the modulation order.

• When you set Constellation ordering to User-defined, specify a vector of size M, which has unique integer values in the range [0, M–1]. The first element of this vector corresponds to the constellation point having an value of e^jϕ with subsequent elements running counterclockwise.

Example: [0 3 2 1]

Constellation mapping — User-defined symbol mapping

[0:7] (default) | vector

User-defined symbol mapping, specified as an M-element vector having unique integer values in the range [0, M – 1]. Use this parameter to specify a custom order for mapping the input integers to output integers.

The first element of this vector corresponds to the constellation point at (0 + ϕ) angle, with subsequent elements running counterclockwise. The last element corresponds to the (-2π/M + ϕ) constellation point. ϕ is the value of phase offset (Phase offset (rad)) and M is the modulation order (M-ary number).

Dependencies

This parameter applies when you set Constellation ordering to User-defined.

Phase offset (rad) — Phase offset in radians

pi/8 (default) | scalar

Specify, in radians, the phase offset of the initial constellation as a real scalar.

Example: pi/4

View constellation — Option to plot reference constellation

button

Click View Constellation on the block mask to visualize a signal constellation for the specified block parameters. Before viewing a constellation, apply the parameter settings. For more information, see View Constellation of Modulator Block.

Data Types

Output data type — Output data type

double (default) | single | Inherit via back propagation | fixdt(1,16) | fixdt(1,16,0) | <data type expression>

Specify the data type of the modulated output signal. Set this parameter to one of the fixed point options or <data type expression> to enable parameters in which you specify additional details. Set this parameter to Inherit via back propagation, to match the output data type and scaling to the following block in the model.

For information about specifying data types, see Data Type Assistant.

Block Characteristics

Data Types	Boolean | double | fixed pointa, b | integer | single
Multidimensional Signals	no
Variable-Size Signals	yes
a ufix(1) at the input if ''input type'' is set to ''bit''. ufix(ceil(log2(M))) at input if ''input type'' is set to ''integer'' for M-ary modulation. b Fixed-point outputs must be signed.

More About

Data Type Assistant

The Data Type Assistant helps you set data attributes. To use the Data Type Assistant, click . For more information, see Specify Data Types Using Data Type Assistant (Simulink).

Algorithms

For higher-order PSK constellations, the complex baseband form for an M-ary PSK signal using binary-ordered symbol mapping is

$$s_m(t)=\exp \left(j\left(\frac{2\pi m}{M}+\varphi \right)\right);m\in \{0,1,\dots ,M-1\}.$$

When the input is configured for bits, groups of log₂(M) bits represent the complex symbols for the configured symbol mapping. The mapping can be binary encoded, Gray encoded, or custom encoded.

Gray coding has the advantage that only one bit changes between adjacent constellation points, which results in better bit error rate performance.

This 8-PSK constellation uses Gray-coded symbol mapping.

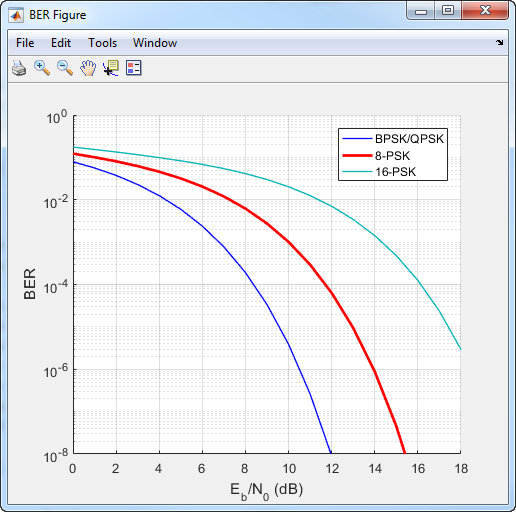
For modulation orders beyond 4, the bit error rate performance of PSK in AWGN worsens. In this bit error rate plot for Gray-coded mapping, the QPSK and BPSK curves overlap one another.

References

[1] Proakis, John G. Digital Communications. 4th ed. New York: McGraw Hill, 2001.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

HDL Code Generation

Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.

HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.

HDL Architecture

This block has one default HDL architecture.

HDL Block Properties

ConstrainedOutputPipeline	Number of registers to place at the outputs by moving existing delays within your design. Distributed pipelining does not redistribute these registers. The default is 0. For more details, see ConstrainedOutputPipeline (HDL Coder).
InputPipeline	Number of input pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see InputPipeline (HDL Coder).
OutputPipeline	Number of output pipeline stages to insert in the generated code. Distributed pipelining and constrained output pipelining can move these registers. The default is 0. For more details, see OutputPipeline (HDL Coder).

Version History

Introduced before R2006a