comm.TurboDecoder
Decode input signal using turbo decoder parallel concatenated decoding scheme
Description
The comm.TurboDecoder
System object™ uses a parallel concatenated decoding scheme to decode a coded input
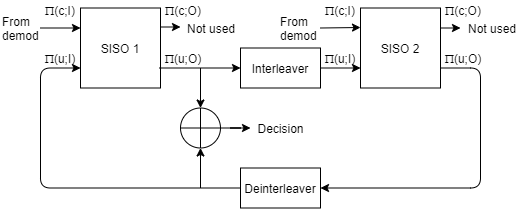
signal. The input signal is typically the soft-decision output from the baseband
demodulation operation. For more information, see Parallel Concatenated Convolutional Decoding Scheme.
To decode an input signal using a parallel concatenated decoding scheme:
Create the
comm.TurboDecoderobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
turbodec = comm.TurboDecoder
turbodec = comm.TurboDecoder(trellis,interlvrindices,numiter)TrellisStructure, InterleaverIndices, and numiter,
respectively. The trellis input must be specified as
described by the TrellisStructure
property. The interlvrindices input must be specified as
described by the InterleaverIndices property. The numiter
input must be specified as described by the NumIterations
property.
turbodec = comm.TurboDecoder(___,Name,Value)comm.TurboDecoder('InterleaverIndicesSource','Input
port') configures a turbo decoder System object with the interleaver indices to be supplied as an input argument
to the System object when it is called.
Properties
Usage
Syntax
Description
decmsg = turbodec(codeword)turbodec returns the binary decoded data. For more
information, see Parallel Concatenated Convolutional Decoding Scheme.
decmsg = turbodec(codeword,interlvrindices)'Input
port'. The interleaver indices define the mapping used to permute
the input at the decoder.
decmsg = turbodec(codeword,interlvrindices,inindices)'Input port'.
The input indices vector values must be relative to the fully encoded data,
including the tail bits for the coding scheme for all streams.
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
References
[1] Benedetto, S., G. Montorsi, D. Divsalar, and F. Pollara. "A Soft-Input Soft-Output Maximum A Posterior (MAP) Module to Decode Parallel and Serial Concatenated Codes." Jet Propulsion Lab TDA Progress Report (November 1996): 42–127.
[2] Viterbi, A.J. “An Intuitive Justification and a Simplified Implementation of the MAP Decoder for Convolutional Codes.” IEEE® Journal on Selected Areas in Communications 16, no. 2 (February 1998): 260–64. https://doi.org/10.1109/49.661114.
[3] Berrou, C., A. Glavieux, and P. Thitimajshima. “Near Shannon Limit Error-Correcting Coding and Decoding: Turbo-Codes.” Proceedings of ICC 93 - IEEE International Conference on Communications, 2: 1064–70. Geneva, Switzerland: IEEE, 1993. https://doi.org/10.1109/icc.1993.397441.
[4] Schlegel, Christian, and Lance Perez. Trellis and Turbo Coding. IEEE Press Series on Digital & Mobile Communication. Piscataway, NJ; Hoboken, NJ: IEEE Press; Wiley-Interscience, 2004.
[5] 3GPP TS 36.212. "Multiplexing and channel coding." 3rd Generation Partnership Project; Technical Specification Group Radio Access Network; Evolved Universal Terrestrial Radio Access (E-UTRA).
Extended Capabilities
Version History
Introduced in R2012a
See Also
Objects
comm.TurboEncoder|comm.ConvolutionalEncoder|comm.APPDecoder|comm.ViterbiDecoder|comm.gpu.TurboDecoder