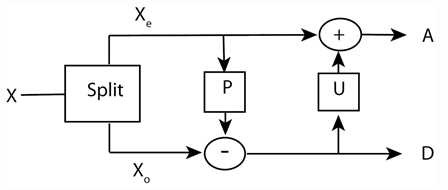
Filterbänke
Orthogonale und biorthogonale Filterbänke sind Anordnungen von Hochpass-, Tiefpass- und Bandpass-Filtern, die Daten in Teilbänder aufteilen. Wenn Sie diese Teilbänder nicht modifizieren, ermöglichen diese Filter eine perfekte Rekonstruktion der Originaldaten. In den meisten Anwendungen verarbeiten Sie die Daten der unterschiedlichen Teilbänder auf verschiedene Weise und rekonstruieren eine modifizierte Version der Originaldaten. Orthogonale Filterbänke weisen keine lineare Phase auf. Biorthogonale Filterbänke weisen eine lineare Phase auf. Sie können Wavelet- und Skalierungsfilter festlegen, indem Sie die Anzahl verschwindender Momente angeben. So können Sie polynomes Verhalten aus Ihren Daten entfernen bzw. in den Daten beibehalten. Mit Lifting können Sie Filterbänke mit perfekter Rekonstruktion mit bestimmten Eigenschaften entwickeln.
Über Wavelet Toolbox™-Funktionen können Sie die gebräuchlichsten orthogonalen und biorthogonalen Wavelet-Filter abrufen und verwenden. Mithilfe von elementaren Lifting-Schritten können Sie eigene Filterbänke mit perfekter Rekonstruktion entwickeln. Zudem können Sie benutzerdefinierte Wavelet-Filter hinzufügen.
Kategorien
- Orthogonale und biorthogonale Filterbänke
Daubechies' Extremal-Phase-, Least-Asymmetric- und Best-Localized-Wavelets, Fejér-Korovkin-Filter, Coiflets, Han Linearphasenfilter, Morris Minimum-Bandwidth-Filter, Beylkin- und Vaidyanathan-Filter, biorthogonale Spline-Filter
- Lifting
1D- und 2D-Lifting, lokale polynomiale Transformationen, Laurent-Polynome
Enthaltene Beispiele
Orthogonal and Biorthogonal Filter Banks
Construct and use orthogonal and biorthogonal filter banks.
Construct Perfect Reconstruction Biorthogonal Filter Bank
Take an expression of a biorthogonal wavelet filter pair and create a perfect reconstruction biorthogonal wavelet filter bank.
Lifting a Filter Bank
Use lifting to progressively change the properties of a perfect reconstruction filter bank.
