GPU Acceleration of Scalograms for Deep Learning
This example shows how you can accelerate scalogram computation using GPUs. The computed scalograms are used as the input features to deep convolution neural networks (CNN) for ECG and spoken digit classification.
Using a GPU requires Parallel Computing Toolbox™. To see which GPUs are supported, see GPU Computing Requirements (Parallel Computing Toolbox). The audio section of this example requires Audio Toolbox™ to use the audio datastore and transformed datastore.
Scalogram Computation Using GPU
The most efficient way to compute scalograms on the GPU is to use cwtfilterbank. The steps to compute scalograms on the GPU are:
Construct
cwtfilterbankwith the desired property settings.Move the signal to the GPU using
gpuArray.Use the filter bank
WTmethod to compute the continuous wavelet transform (CWT).
The first time you use the WT method, cwtfilterbank caches the wavelet filters on the GPU. As a result, substantial time savings in computation are realized when you obtain scalograms of multiple signals using the same filter bank and same datatype. The following demonstrates the recommended workflow. As an example, use a sample of guitar music containing 661,500 samples.
[y,fs] = audioread('guitartune.wav'); plot(y) grid on

Because most NVIDIA® GPUs are significantly more efficient with single rather than double-precision data, cast the signal to single precision.
y = single(y);
Construct the filter bank to match the signal length and the sampling frequency. For deep learning, the sampling frequency is normally not necessary and therefore can be excluded.
fb = cwtfilterbank('SignalLength',length(y),'SamplingFrequency',fs);
Finally move the signal to the GPU using gpuArray and compute the CWT of the data. Plot the resulting scalogram.
[cfs,f] = fb.wt(gpuArray(y)); t = 0:1/fs:(length(y)*1/fs)-1/fs; imagesc(t,f,abs(cfs)) axis xy ylabel('Hz') xlabel('Seconds')

Use gather to bring the CWT coefficients and any other outputs back to the CPU.
cfs = gather(cfs); f = gather(f);
To demonstrate the efficiency gained in using the GPU, time the CWT computation on the GPU and CPU for the same signal. The GPU compute times reported here are obtained using an NVIDIA Titan V with a compute capability of 7.0.
ygpu = gpuArray(y); fgpu = @()fb.wt(ygpu); Tgpu = gputimeit(fgpu)
Tgpu = 0.3503
Repeat the same measurement on the CPU and examine the ratio of GPU to CPU time to see the reduction in computation time.
fcpu = @()fb.wt(y); Tcpu = timeit(fcpu)
Tcpu = 4.3036
Tcpu/Tgpu
ans = 12.2852
Scalograms in Deep Learning
A common application of the CWT in deep learning is to use the scalogram of a signal as the input "image" to a deep CNN. This necessarily mandates the computation of multiple scalograms, one for each signal in the training, validation, and test sets. While GPUs are often used to speed up training and inference in the deep network, it is also beneficial to use GPUs to accelerate any feature extraction, or data preprocessing needed to make the deep network more robust.
To illustrate this, the following section applies wavelet scalograms to human electrocardiogram (ECG) classification. Scalograms are used with the same data treated in Classify Time Series Using Wavelet Analysis and Deep Learning. In that example, transfer learning with GoogLeNet and SqueezeNet was used to classify ECG waveforms into one of three categories. The description of the data and how to obtain it is repeated here for convenience.
ECG Data Description and Download
The ECG data is obtained from three groups of people: persons with cardiac arrhythmia (ARR), persons with congestive heart failure (CHF), and persons with normal sinus rhythms (NSR). In total there are 162 ECG recordings from three PhysioNet databases: MIT-BIH Arrhythmia Database [2][3], MIT-BIH Normal Sinus Rhythm Database [3], and The BIDMC Congestive Heart Failure Database [1][3]. More specifically, 96 recordings from persons with arrhythmia, 30 recordings from persons with congestive heart failure, and 36 recordings from persons with normal sinus rhythms. The goal is to train a model to distinguish between ARR, CHF, and NSR.
You can obtain this data from the MathWorks GitHub repository. To download the data from the website, click Code and select Download ZIP. Save the file physionet_ECG_data-main.zip in a folder where you have write permission. The instructions for this example assume you have downloaded the file to your temporary directory, tempdir, in MATLAB®. Modify the subsequent instructions for unzipping and loading the data if you choose to download the data in folder different from tempdir.
After downloading the data from GitHub, unzip the file in your temporary directory.
unzip(fullfile(tempdir,'physionet_ECG_data-main.zip'),tempdir)Unzipping creates the folder physionet-ECG_data-main in your temporary directory. This folder contains the text file README.md and ECGData.zip. The ECGData.zip file contains
ECGData.matModified_physionet_data.txtLicense.txt
ECGData.mat holds the data used in this example. The text file, Modified_physionet_data.txt, is required by PhysioNet's copying policy and provides the source attributions for the data as well as a description of the preprocessing steps applied to each ECG recording.
Unzip ECGData.zip in physionet-ECG_data-main. Load the data file into your MATLAB workspace.
unzip(fullfile(tempdir,'physionet_ECG_data-main','ECGData.zip'),... fullfile(tempdir,'physionet_ECG_data-main')) load(fullfile(tempdir,'physionet_ECG_data-main','ECGData.mat'))
ECGData is a structure array with two fields: Data and Labels. The Data field is a 162-by-65536 matrix where each row is an ECG recording sampled at 128 hertz. Labels is a 162-by-1 cell array of diagnostic labels, one for each row of Data. The three diagnostic categories are: 'ARR', 'CHF', and 'NSR'. Use the helper function, helperRandomSplit, to split the data into training and validation sets with 80% of the data allocated for training and 20% for validation. Convert the ECG diagnostic labels into categoricals.
[trainData, validationData, trainLabels, validationLabels] = helperRandomSplit(80,ECGData); trainLabels = categorical(trainLabels); validationLabels = categorical(validationLabels);
There are 130 records in the trainData set and 32 records in validationData. By design, the training data contains 80.25% (130/162) of the data. Recall that the ARR class represents 59.26% of the data (96/162), the CHF class represents 18.52% (30/162), and the NSR class represents 22.22% (36/162). Examine the percentage of each class in the training and test sets. The percentages in each are consistent with the overall class percentages in the data set.
Ctrain = countcats(trainLabels)./numel(trainLabels).*100
Ctrain = 3×1
59.2308
18.4615
22.3077
Cvalid = countcats(validationLabels)./numel(validationLabels).*100
Cvalid = 3×1
59.3750
18.7500
21.8750
Scalograms With Deep CNN — ECG Data
Scalogram Computation on the GPU
Compute the scalograms for both the training and validation sets. Set useGPU to true to use the GPU and false to compute the scalograms on the CPU. To mitigate the effect of large input matrices on the CNN and create more training and validation examples, helperECGScalograms splits each ECG waveform into four nonoverlapping segments of 16384 samples each and computes scalograms for all four segments. Replicate the labels to match the expanded dataset. In this case, obtain an estimate of the expended computation time.
frameLength = 16384; useGPU = true; tic; Xtrain = helperECGScalograms(trainData,frameLength,useGPU);
Computing scalograms... Processed 50 files out of 130 Processed 100 files out of 130 ...done
T = toc;
sprintf('Elapsed time is %1.2f seconds',T)ans = 'Elapsed time is 4.59 seconds'
trainLabels = repelem(trainLabels,4);
With the Titan V GPU, 502 scalograms have been computed in approximately 4.2 seconds. Setting useGPU to false and repeating the above computation demonstrates the speed up obtained by using the GPU. In this case, using the CPU required 33.3 seconds to compute the scalograms. The GPU computation was more than 7 times faster.
Repeat the same process for the validation data.
useGPU = true; Xvalid = helperECGScalograms(validationData,frameLength,useGPU);
Computing scalograms... ...done
validationLabels = repelem(validationLabels,4);
Next set up a deep CNN to process both the training and validation sets. The simple network used here is not optimized. This CNN is only used to illustrate the end-to-end workflow for cases where the scalograms fit in memory.
sz = size(Xtrain);
specSize = sz(1:2);
imageSize = [specSize 1];
dropoutProb = 0.3;
layers = [
imageInputLayer(imageSize)
convolution2dLayer(3,12,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(2,'Stride',2)
convolution2dLayer(3,20,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(2,'Stride',2)
convolution2dLayer(3,32,'Padding','same')
batchNormalizationLayer
reluLayer
dropoutLayer(dropoutProb)
fullyConnectedLayer(3)
softmaxLayer
];Use the following training options.
options = trainingOptions('sgdm', ... 'InitialLearnRate',1e-4, ... 'LearnRateDropPeriod',18, ... 'MiniBatchSize',15, ... 'MaxEpochs',25, ... 'L2Regularization',1e-1, ... 'Plots','training-progress', ... 'Metrics','accuracy', ... 'Verbose',false, ... 'Shuffle','every-epoch', ... 'ExecutionEnvironment','auto', ... 'ValidationData',{Xvalid,validationLabels});
Train the network and measure the validation error.
trainnet(Xtrain,trainLabels,layers,"crossentropy",options);
Even though the simple CNN used here is not optimized, the validation accuracy is consistently in the high 80 to low 90 percent range. This is comparable to the validation accuracy achieved with the more powerful and optimized SqueezeNet shown in Classify Time Series Using Wavelet Analysis and Deep Learning example. Further, this is a much more efficient use of the scalogram, because in that example the scalograms had to be rescaled as RGB images compatible with SqueezeNet, saved to disk in an appropriate image format, and then fed to the deep network using imageDatastore.
Spoken Digit Recognition — GPU Computing using Transform Datastore
This section shows how to accelerate scalogram computation using GPU in a transformed datastore workflow.
Data
Download the Free Spoken Digit Dataset (FSDD). FSDD consists of 2000 recordings in English of the digits 0 through 9 obtained from four speakers. Two of the speakers are native speakers of American English, one speaker is a nonnative speaker of English with a Belgian French accent, and one speaker is a nonnative speaker of English with a German accent. The data is sampled at 8000 Hz.
downloadFolder = matlab.internal.examples.downloadSupportFile("audio","FSDD.zip"); dataFolder = tempdir; unzip(downloadFolder,dataFolder) dataset = fullfile(dataFolder,"FSDD");
Use audioDatastore to manage data access.
ads = audioDatastore(dataset,IncludeSubfolders=true);
The helper function helpergenLabels creates a categorical array of labels from the FSDD files. List the classes and the number of examples in each class.
ads.Labels = helpergenLabels(ads); summary(ads.Labels)
0 200
1 200
2 200
3 200
4 200
5 200
6 200
7 200
8 200
9 200
Transformed Datastore
First split the FSDD into training and test sets. Allocate 80% of the data to the training set and retain 20% for the test set.
rng default;
ads = shuffle(ads);
[adsTrain,adsTest] = splitEachLabel(ads,0.8);
countEachLabel(adsTrain)ans=10×2 table
Label Count
_____ _____
0 160
1 160
2 160
3 160
4 160
5 160
6 160
7 160
8 160
9 160
Next create the CWT filter bank and the transformed datastores for both the training and test data using the helper function, helperDigitScalogram. The transformed datastore converts each recording into a signal of length 8192, computes the scalogram on the GPU, and gathers the data back onto the CPU.
reset(gpuDevice(1)) fb = cwtfilterbank('SignalLength',8192); adsSCTrain = transform(adsTrain,@(audio,info)helperDigitScalogram(audio,info,fb),'IncludeInfo',true); adsSCTest = transform(adsTest,@(audio,info)helperDigitScalogram(audio,info,fb),'IncludeInfo',true);
Deep CNN
Construct a deep CNN to train with the transformed datastore, adscTrain. As in the first example, the network is not optimized. The point is to show the workflow using scalograms computed on the GPU for out-of-memory data.
numClasses = 10;
dropoutProb = 0.2;
numF = 12;
layers = [
imageInputLayer([101 8192 1])
convolution2dLayer(5,numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,2*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(3,'Stride',2,'Padding','same')
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
convolution2dLayer(3,4*numF,'Padding','same')
batchNormalizationLayer
reluLayer
maxPooling2dLayer(2)
dropoutLayer(dropoutProb)
fullyConnectedLayer(numClasses)
softmaxLayer
]; Set the training options for the network.
miniBatchSize = 25; options = trainingOptions('adam', ... 'InitialLearnRate',1e-4, ... 'MaxEpochs',30, ... 'MiniBatchSize',miniBatchSize, ... 'Shuffle','every-epoch', ... 'Plots', 'training-progress',... 'Metrics','accuracy', ... 'Verbose',false,... 'ExecutionEnvironment','gpu');
Train the network.
trainedNet = trainnet(adsSCTrain,layers,"crossentropy",options);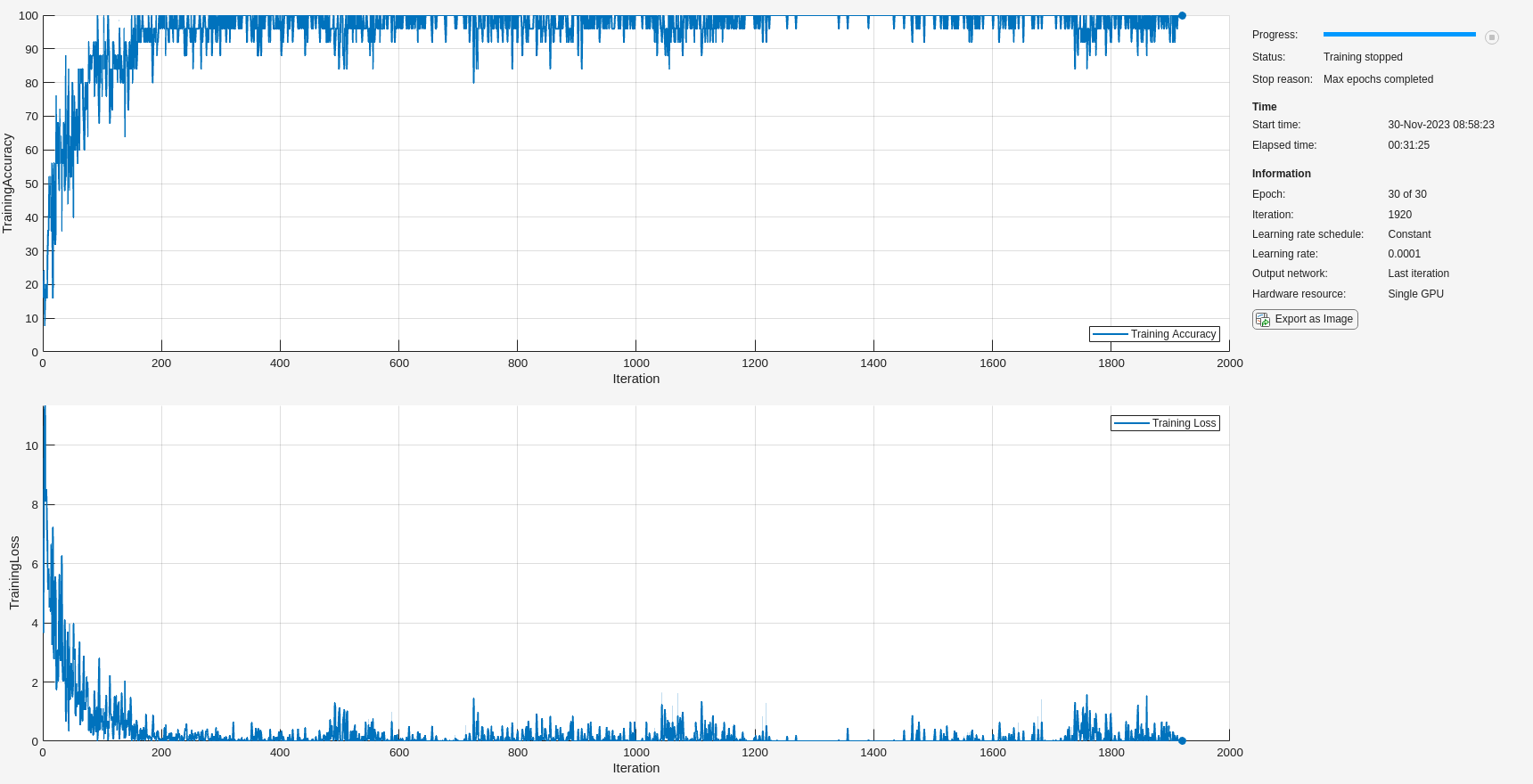
In this instance, training was completed in around 30 minutes. If you comment out the call to gpuArray in helperDigitScalogram and use the CPU to obtain the scalograms, training time increases significantly. In this case, an increase from 30 minutes to 55 minutes was observed.
Use the trained network to predict the digit labels for the test set.
score = minibatchpredict(trainedNet,adsSCTest,'ExecutionEnvironment','cpu'); classNames = categories(ads.Labels); Ypredicted = scores2label(score,classNames); cnnAccuracy = sum(Ypredicted == adsTest.Labels)/numel(Ypredicted)*100
cnnAccuracy = 93.5000
The inference time using the GPU was approximately 22 seconds. Using the CPU, inference time doubled to 45 seconds.
The performance of trained network on the test data is around 90%. This is comparable to the performance in Spoken Digit Recognition with Wavelet Scattering and Deep Learning.
Summary
This example has showcased how to use the GPU to accelerate scalogram computation. The example presented the optimal workflow for efficiently computing scalograms both for in-memory data and for out-of-memory data read from disk using transformed datastores.
References
Baim, D. S., W. S. Colucci, E. S. Monrad, H. S. Smith, R. F. Wright, A. Lanoue, D. F. Gauthier, B. J. Ransil, W. Grossman, and E. Braunwald. "Survival of patients with severe congestive heart failure treated with oral milrinone." Journal of the American College of Cardiology. Vol. 7, Number 3, 1986, pp. 661–670.
Goldberger A. L., L. A. N. Amaral, L. Glass, J. M. Hausdorff, P. Ch. Ivanov, R. G. Mark, J. E. Mietus, G. B. Moody, C.-K. Peng, and H. E. Stanley. "PhysioBank, PhysioToolkit,and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals." Circulation. Vol. 101, Number 23: e215–e220. [Circulation Electronic Pages;
http://circ.ahajournals.org/content/101/23/e215.full]; 2000 (June 13). doi: 10.1161/01.CIR.101.23.e215.Moody, G. B., and R. G. Mark. "The impact of the MIT-BIH Arrhythmia Database." IEEE Engineering in Medicine and Biology Magazine. Vol. 20. Number 3, May-June 2001, pp. 45–50. (PMID: 11446209)
Helper Functions
function Labels = helpergenLabels(ads) % This function is only for use in Wavelet Toolbox examples. It may be % changed or removed in a future release. tmp = cell(numel(ads.Files),1); expression = "[0-9]+_"; for nf = 1:numel(ads.Files) idx = regexp(ads.Files{nf},expression); tmp{nf} = ads.Files{nf}(idx); end Labels = categorical(tmp); end
function X = helperECGScalograms(data,window,useGPU) disp("Computing scalograms..."); Nsig = size(data,1); Nsamp = size(data,2); Nsegment = Nsamp/window; fb = cwtfilterbank('SignalLength',window,'Voices',10); Ns = length(fb.Scales); X = zeros([Ns,window,1,Nsig*Nsegment],'single'); start = 0; if useGPU data = gpuArray(single(data')); else data = single(data'); end for ii = 1:Nsig ts = data(:,ii); ts = reshape(ts,window,Nsegment); ts = (ts-mean(ts))./max(abs(ts)); for kk = 1:size(ts,2) cfs = fb.wt(ts(:,kk)); X(:,:,1,kk+start) = gather(abs(cfs)); end start = start+Nsegment; if mod(ii,50) == 0 disp("Processed " + ii + " files out of " + Nsig) end end disp("...done"); data = gather(data); end
function [x,info] = helperReadSPData(x,info) % This function is only for use Wavelet Toolbox examples. It may change or % be removed in a future release. N = numel(x); if N > 8192 x = x(1:8192); elseif N < 8192 pad = 8192-N; prepad = floor(pad/2); postpad = ceil(pad/2); x = [zeros(prepad,1) ; x ; zeros(postpad,1)]; end x = x./max(abs(x)); end
function [dataout,info] = helperDigitScalogram(audioin,info,fb) audioin = single(audioin); audioin = gpuArray(audioin); audioin = helperReadSPData(audioin); cfs = gather(abs(fb.wt(audioin))); audioin = gather(audioin); dataout = {cfs,info.Label}; end